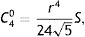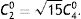The aim of this work was to examine the impact of Seidel spherical aberration (SA) on optimum refractive state for detecting and discriminating small bright lights on a dark background.
MethodsAn adaptive-optics system was used to correct ocular aberrations of cyclopleged eyes and then systematically introduce five levels of Seidel SA for a 7-mm diameter pupil: 0,±0.18, and±0.36diopters (D)mm−2. For each level of SA, subjects were required to detect one or resolve two points of light (0.54 arc min diameter) on a dark background. Refractive error was measured by adjusting stimulus vergence to minimize detection and resolution thresholds. Two other novel focusing tasks for single points of light required maximizing the perceived intensity of a bright point's core and minimizing its overall perceived size (i.e. minimize starburst artifacts). Except for the detection task, luminance of the point of light was 1000cdm−2 on a black background lower than 0.5cdm−2.
ResultsPositive SA introduced myopic shifts relative to the best subjective focus for dark letters on a bright background when there was no SA, whereas negative SA introduced hyperopic shifts in optimal focus. The changes in optimal focus were −1.7, −2.4, −2.0, and −9.2D of focus per Dmm−2 of SA for the detection task, resolution task, and maximization of core's intensity and minimization of size, respectively.
ConclusionOcular SA can be a significant contributor to changes in refractive state when viewing high-contrast point sources typically encountered in nighttime environments.
El objetivo de este estudio fue examinar el impacto de la aberración esférica de Seidel (AS) sobre el estado refractivo óptimo para detectar y discriminar las luces brillantes de pequeño tamaño sobre un fondo oscuro.
MétodosSe utilizó un sistema de óptica adaptativa para corregir las aberraciones oculares de ojos bajo cicloplegía, e introducir sistemáticamente cinco valores de AS para una pupila de 7mm de diámetro: 0,±0,18, y±0,36 dioptrías (D) mm−2. Para cada valor de AS se solicitó a los sujetos que detectaran un punto de luz, o resolvieran dos puntos (cada punto subtendía 0,54 minutos de arco de diámetro) sobre un fondo oscuro. El error refractivo se midió ajustando la vergencia del estímulo, para minimizar los umbrales de detección y resolución. Los sujetos realizaron además otras dos tareas observando un sólo punto luminoso y en las que tenían que maximizar la intensidad percibida del núcleo del punto luminoso o minimizar el tamaño de la imagen percibida (es decir, minimizar el “starburst”). Excepto para la tarea de detección, la luminancia del punto de luz fue de 1000cd m−2 sobre un fondo negro con un valor inferior a 0,5cd m−2.
ResultadosLa AS positiva introdujo cambios miópicos respecto al mejor enfoque subjetivo para letras oscuras sobre un fondo luminoso sin AS, mientras que la AS negativa introdujo cambios hipermetrópicos respecto al enfoque óptimo. Estos cambios fueron−1,7,−2,4,−2,0, y−9,2 D de enfoque por D mm−2 de AS para la tarea de detección, la tarea de resolución, la maximización de la intensidad del núcleo y la minimización de su tamaño, respectivamente.
ConclusiónLa AS ocular puede ser un factor que influye significativamente en los cambios en el estado refractivo, al visualizar las fuentes puntuales de alto contraste típicas de los entornos nocturnos.
Spherical aberration (SA) is a dominant higher-order aberration in human eyes1,2 that creates local refractive errors proportional to the square of radial distance from the pupil center.3,4 As a result, the pupil margin can be as much as 3diopters (D) more myopic than the pupil center for an 8-mm diameter pupil, typical of nighttime viewing.4 Inclusion of these more myopic regions as the pupil dilates, however, has little or no measurable impact on subjective refraction,5–8 revealing that subjective refractions are dominated by the refractive state of the central pupil region.9
When refracted with high contrast small letters, even large amounts of experimentally added positive SA (with fixed pupil size and no accommodation) produced only minor myopic shifts in subjective refractive errors, and added negative SA produces small hyperopic shifts.10,11 However, the magnitudes of these shifts varied significantly with the stimulus and the visual task used in the refraction procedure. For example, SA has its smallest effect when best focus is determined by optimizing letter acuity or by optimizing perceived quality of objects dominated by high spatial frequencies.11 However, the effect of SA is much larger when optimizing perceived quality of stimuli dominated by low spatial frequencies.7,11 The perceptual criterion used for optimizing focus is also important. The impact of SA on refractive error is greater when subjects optimized perceived contrast of letters than when optimizing perceived sharpness of the same letters. López-Gil et al.12 observed a myopic shift in refractive error of eyes when changing the stimulus from a letter chart to a small bright point source viewed against a dark background. These changes were partially due to accommodation, but were correlated with the magnitude of SA in the different subjects’ eyes, with a R2 of 0.55.
Given the importance of stimulus, task, and criterion for determining refractive state in eyes with spherical aberration, we asked if the myopic shifts commonly reported by stargazers,13–15 might be due in part to the presence of elevated positive spherical aberration (characteristic of large nighttime pupils) coupled with the change from extended objects with limited contrast commonly encountered during daytime viewing to very high contrast point sources of light viewed against a dark background commonly encountered at night? We pursued this question with adaptive optics to correct the eye's native aberrations and systematically introduce controlled amounts of Seidel SA (which has no effect on paraxial focus) while experimentally measuring refractive state for point sources of light displayed in an otherwise dark field. Subjects optimized focus in four separate tasks: detection of a single bright point, resolution of two bright points, maximization of the perceived intensity of the core of the image of a bright point and minimization of the overall perceived size of the image of a bright point. The last task is equivalent to minimizing starburst artifacts around the point of light.16,17 The results of this study revealed a systematic effect of SA on refractive state that depends on the sign and magnitude of the aberration as well as the task and criterion used for judging best focus. These effects were consistent with predictions based on established objective metrics of retinal image quality for point sources of light.
MethodsApparatusAn adaptive-optics (AO) system built in the Universidad de Murcia was used to correct spherical refractive error, astigmatism, and higher-order aberrations, and then induce different amounts of positive and negative Seidel SA. The AO system consisted of a Shack–Hartmann wavefront sensor with 40×32 micro-lenses (HASO32, Imagine Eyes) and a deformable mirror (Mirao 52e, Imagine Eyes). A low-intensity (102.5μW) near-infrared beam of light (830nm) was used to take measurements of eye's aberrations. More details of the optical system have been published elsewhere.18,19 The AO system corrects and induces higher-order aberrations with sufficient precision: the root mean square error between target and measured wavefronts achieved with our AO system were typically about 0.15μm over the dilated pupil of the observer of over 7mm of diameter. The correction was stable over time. Subjects viewed the stimuli on an 800×600 microdisplay (SVGA+OLED micro-display, eMagin) through a 7-mm artificial pupil made conjugate with the eye's entrance pupil. The effective display luminance for the full contrast spots was determined by absorption and reflections from all of the intervening optics, resulting in test stimuli with spot luminance of about 1000cdm−2 and a background luminance of <0.5cdm−2. Each spot was made up of 2×2 pixels, and subtended 0.54arc min at the pupil plane. The microdisplay nonlinearities were gamma corrected before the experiment. A user-controlled Badal system allowed stimulus vergence to be changed automatically with a computer program in the detection and resolution tasks and by the subject in the smallest core and overall perceived size refraction tasks. The working range of the Badal system was greater than 10D. A bite bar was used to restrain head movements as much as possible and to align the eye with the optical system.
SubjectsThree subjects with ages 29, 38, and 47, spherical refractive error 0.5D, 0.25D, and −3.25D, respectively, and less than 1D of astigmatism, participated in the experiment. The eyes tested had clear optics and no ocular or systematic diseases. To achieve long-lasting pupil dilation effects (a pupil greater than 7mm diameter) and paralyzed accommodation needed for this study, two drops of 1% tropicamide were instilled with 5min between each drop. After correcting for astigmatism and higher-order aberrations with AO, subjective refractions were obtained for the cyclopleged eyes with a user-controlled Badal system and small high-contrast Snellen letters presented in the micro-display with different sizes for each level of SA induced. Subjects were asked to adjust stimulus vergence to achieve best subjective focus of the Snellen letters. Each subject repeated this task five times for each level of SA induced and the mean value calculated. Best subjective focus for the SA=0 condition was taken as the reference value of zero defocus for reporting the experimental results.
Experimental protocols were approved by the University institutional review board. Consent was obtained from all subjects after the purpose and experimental methods were described. The experiment adhered to the tenets of the Declaration of Helsinki.
Experimental proceduresEach subject performed four experiments for five different levels of Seidel SA (presented in random order) induced for a 7-mm artificial pupil. Seidel SA provides zero refractive power at the pupil center, but for other points in the eye's pupil refractive power is proportional to the square of the distance from the pupil center. Thus the refractive strength S of the aberration is quantified in units of D mm−2, a measure that is independent of pupil diameter. The five levels of Seidel SA were −0.36, −0.18, 0, 0.18, and 0.36Dmm−2. The rationale for quantifying SA this way is perhaps best understood by analogy with mechanics. Just as location of a moving object can be proportional to time (i.e. constant velocity in ms−1) or to the square of time (constant acceleration in ms−2), refractive power or wavefront vergence of an aberrated eye can be proportional to distance from the pupil center (e.g. coma, in D mm−1), or to the square of distance (e.g. SA, in D mm−2). Thus, the power of the marginal rays for a 7-mm pupil is 1.1D for a Seidel SA of 0.18D mm−2 and 2.2D for Seidel SA of 0.36D mm−2. To program the AO system for a pupil of radius r, pre-determined values of S were converted to Zernike aberration coefficients C40 (Zernike SA) and C20 (Zernike defocus) thus20,21:
Both Zernike coefficients are given in microns. For example, for a 7mm pupil diameter, to produce S=0.36Dmm−2 of Seidel SA requires C40=1 μm and C20=3.87 μm. The five levels of Seidel SA correspond, thus, to 0,±0.5 and, ±1μm of Zernike SA for a 7-mm pupil. We selected these rather extreme values to show a clear and measurable effect in the point-spread function (PSF) based on our prior experience.9,11,17
All experiments were performed monocularly while the contralateral eye was covered with an eye patch. It took about 2hours to complete all experiments and breaks were taken as necessary at the subject's request. Two of the subjects had prior experience with similar experiments and the third subject underwent several training sessions until he was confident to have understood the tasks to perform in each experiment and became acquainted with the psychophysical paradigm. Dilated pupil diameters remained larger than 7mm throughout the experiment. Before each trial, full aberration correction and the desired level of SA were introduced with the AO system. We did not monitor the wavefront manipulation of the AO system during the trial because the light of the diode used to measure the aberrations would have interfered with the psychophysical task.
Experiment 1. Two-point resolutionSubjects’ task was to increase the separation of two bright spots of light, each of which were 0.54 arc min in diameter, until they could be resolved. The two points had an intensity of about 1000cdm−2 and initially abutted each other, that is, separation between them was zero. They were presented on a black background lower than 0.5cdm−2. Using ascending methods of limits, subjects were instructed to increase the distance until they saw a clear separation between the spots of light. The minimum angular separation between the centers of the two spots is defined as two-point resolution in arc min.22 The resolution task was performed for 13 vergences varying from −1.5D to 1.5D in steps of 0.25D relative to best subjective focus for the Snellen letter chart for the corresponding amount of SA and with spots randomly separated horizontally, vertically, or diagonally to obtain 4 through-focus curves of discrimination thresholds, one for each direction of separation. The room lights were turned off and the amount of SA and defocus induced was randomized in each trial.
A through-focus curve with its 68% confidence band for resolution was obtained as the average over the four directions of separation and ±1 standard error of the mean (SEM). A smoothing technique, robust loess23 with a span parameter of 0.85, was applied to the average thresholds and SEM. This method implicitly assumes that changes in threshold and SEM are continuous functions of stimulus vergence. Optimal refraction was obtained from the smoothed through-focus curves after selecting an interval of threshold points considered to be equally valid candidates for optimal refraction.8 Thus, all vergence points that had thresholds with 68% confidence intervals (−1 SEM) that overlap with the 68% confidence interval (+1 SEM) for the smallest threshold were selected. Optimal refraction was the median of that range of selected vergence points. Fig. 1 illustrates the procedure to obtain the optimal refraction.
Calculation of the optimal refraction for a sample through-focus resolution curve for a subject with an induced Seidel SA of 0.38Dmm−2 for a 7-mm pupil. The left panel shows the average resolution thresholds (open circles) and ±1 SEM over 4 directions of separation at each stimulus vergence. The solid black curve shows the loess fit. The red horizontal line shows the estimated threshold. The right panel shows the smoothed luminance threshold (open and solid circles) and ±1 smoothed SEM. The red horizontal line is the cutoff set by the minimum resolution threshold +its SEM. The black solid circles in the right panel are those thresholds that fall below the cutoff set by the red line after subtracting their SEM. The optimal refraction for this is the median of all selected thresholds (black solid circles).
With this criterion for optimal refraction, if SEM was constant over all vergences in the through-focus curve, the maximum distance between the minimum threshold and all other thresholds selected would be 2 SEM, corresponding to a Gaussian confidence interval of 95%.
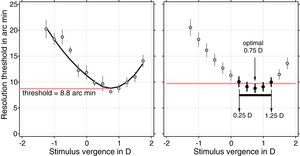
Experiment 2. Single spot of light detectionA single 0.54 arc min diameter spot was presented on a black background lower than 0.5cdm−2. The spot of light was initially set to have the same luminance as the background. Using ascending methods of limits, subjects’ task was to increase the luminance of the spot until they detected it, which was defined as the detection threshold in this study. The detection task was performed for 13 vergences varying from −1.5D to 1.5D in steps of 0.25D relative to the best subjective focus for the Snellen letter chart for the corresponding amount of SA. The experiment was repeated 3 times at each vergence and each SA level.
Using the same data analysis procedure described above for the resolution task, we obtained optimal refractions from the average through-focus detection curves (see Fig. 2).
Experiment 3. Smallest coreUsing the subjective appearance of a 0.54 arc min spot of light with 1000cdm−2 of intensity presented on a black background lower than 0.5cdm−2, subjects were instructed to adjust the stimulus vergence until the perceived intensity of its core was greatest. Subjects typically reported observing a starburst pattern surrounding this small bright core. The experiment was repeated 3 times for each SA level.
Experiment 4. Smallest overall sizeIn the same experimental condition as Experiment 3, subjects were instructed to adjust stimulus vergence until the overall perceived size, including the radiating starbursts, was at its smallest. The experiment was repeated 3 times for each SA level.
Computer modelingThrough-focus curves for a high spatial frequency biased metric of image quality, the visual Strehl ratio from the monochromatic optical transfer function (VSOTF),24 were computed for an aberration-free optical model to which SA was added. The model included pupil apodization that emulates the pupil weighting function observed psychophysically as the Stiles-Crawford Effect.9 Model predictions were included also for refractive corrections that minimize wavefront root mean square (RMS) error, focus the pupil margin, and minimize the geometrical PSF size.9,25
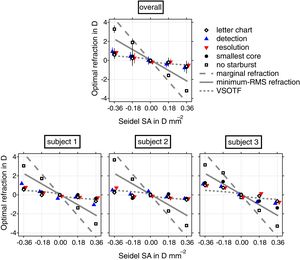
Results and commentAverage subjective refractions for all four refractive error criteria are plotted as a function of induced SA in Fig. 3. All refractions are referenced to the aberration free spherical refraction when viewing high contrast black letters on a high-luminance white background. For comparison purposes, the minimum-RMS refraction (solid gray line), the marginal refraction (dashed gray line), and the optimal image quality refraction obtained with the VSOTF metric (dotted gray line) are also shown. By design, optimal paraxial refraction is always zero regardless of the amount of Seidel SA induced.
Difference in refractive error between paraxial refraction and the four different refractive criteria as a function of Seidel SA for a 7-mm pupil. The top panel shows refractions averaged (±2 SEM) over the 3 subjects. The bottom panel shows the average refractions for each subject over the 4 different directions for the detection task and over the 3 repetitions for the rest of the tasks. Best aberration-corrected subjective refraction for Snellen letter chart (diamonds) are shown for reference. Lines represent three model predictions.
Relative to paraxial refraction, optimal refractions varied with SA at a rate of −1.6D of defocus per Dmm−2 of SA for the best subjective refraction of the Snellen letter chart, −1.7D of defocus per Dmm−2 of SA for the resolution task, −2.4D per Dmm−2 for the detection task, −2.0D per Dmm−2 to maximize perceived intensity of the bright point's core, and −9.2D per Dmm−2 to minimize overall perceived size including the radiating starbursts. Minimum-RMS refraction predicted by the optical model varied by about −6.1D per Dmm−2 of SA and marginal refraction by twice as much at −12.2D per Dmm−2 of SA. VSOTF refraction varied by about −1.6D per Dmm−2 of SA.
Subjective refractions for Snellen letter chart, maximizing two-point resolution and minimizing perceived intensity were best predicted by the VSOTF metric. Refractions that optimized spot detection were affected slightly more by SA levels, but much less than minimum-RMS refractions. Refractions that removed starbursts by subjectively minimizing the overall size of the PSF were approximately three quarters of those that focused the pupil margins, as predicted by geometrical optics.17,25 For all six methods of refraction, positive SA produced equal but opposite sign changes in refractive error to those generated by negative SA. Although the VSOTF predicted refractions generally matched the subjective refractions for Snellen letters, maximizing two-point resolution and minimizing perceived intensity, refractions for subject 3 with negative Seidel SA were systematically more hyperopic than predicted.
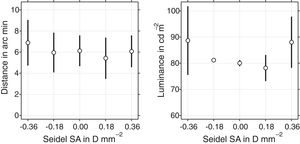
Through-focus curves for two-point resolution (Fig. 1) and one-point detection tasks (Fig. 2) also reveal the impact of SA on optimal performance. Fig. 4 shows the average resolution and detection thresholds over the three subjects when the eye is optimally focused for each level of Seidel SA. In this optimally-focused condition, SA had no consistent effect on two-point resolution (threshold separation was on average close to 6 arc min for all levels of Seidel SA).
The main effect of SA on detection was to increase between-subject variance. Mean detection threshold was close to 80cdm−2 for −0.18, 0, and +0.18Dmm−2 of Seidel SA and about 10% greater at 90cdm−2 for both −0.36 and +0.36Dmm−2 of Seidel SA.
DiscussionThe wavefront errors generated by ocular SA vary with the fourth power of pupil radius and therefore wavefront vergence errors associated with excess dioptric power vary with the square of pupil radius.4,9 A long-standing puzzle is that, in spite of this quadratic increase of excess refractive power exposed at the pupil margins by pupil dilation, subjective refractions remain unchanged for photopic stimuli as pupils dilate.5–8 A classic piece of the puzzle is that pupil dilation under scotopic viewing conditions produced significant myopic shifts in subjective refractions.6 Those scotopic results revealed a potential role for positive ocular SA in night or twilight myopia when vision is supported by rod photoreceptors. Significantly, low mean luminance levels are not the only signature of the nighttime environment, which is also replete with small bright (photopic) point light sources, such as stars, streetlights, and car headlights, within an otherwise scotopic background. This feature of the nighttime environment may also have a role in the observed night and twilight myopias. A recent study12 observed a myopic shift in subjective refractions when switching from a letter chart to a small bright point source on a dark background. These classic studies provided the framework for our investigation of refractive shifts associated with nighttime viewing and the relative importance of visual task, visual target, and ocular aberrations.
The present study was designed to systematically assess whether small bright spots of light will always lead to myopic shifts in subjective refractions, or if such shifts are related to the levels and sign of SA. Because the impact of SA on subjective refraction has been shown to vary with task and criterion,11,12 four different tasks and criteria were chosen for determining best subjective focus for these small and bright point sources. The results show that small point sources will generate myopic shifts in subjective refractions, but only in the presence of positive SA. The opposite result is obtained when SA is negative: refractive shifts are in the hyperopic direction, an effect that can be called night hyperopia. The magnitude of these shifts depends critically on the task given to the subjects. Since unaccommodated eyes typically exhibit positive SA, SA may be a contributing factor to the myopic shift observed when viewing small bright lights in an otherwise dark environment,15 often referred to as night or twilight myopia.12,14,26,27 Interestingly, SA is near zero28 in most eyes when they accommodate moderately (at about 2D), typically corresponding to resting point in total darkness.29,30 Under those conditions, an apparent but spurious myopia may be present at night due to accommodation.31
The lack of effect of SA on visual acuity observed here (see the resolution thresholds in left panel of Fig. 4) is in agreement with previous observations.32 The lack of effect of SA in detection threshold at ±0.18Dmm−2 of SA and increase at ±0.36D may be explained by the relative size of the PSF and Ricco's area. Changes in threshold would only be expected for values of SA large enough for light to spread out beyond Ricco's area.
A previous study11 showed that positive SA was always associated with myopic shifts with average slope values of −2.0D per Dmm−2 of Seidel SA, which are similar to the values reported in the current study with a Snellen letter chart (−1.6D per Dmm−2), and two-point resolution (−1.7D per Dmm−2) and spot detection tasks (−2.4D per Dmm−2) as well as the subjective criterion of maximizing the core brightness (−2.0D per Dmm−2). This agreement indicates that refractive shifts obtained for spots of light are much the same as for letter charts, and other stimuli typical of a photopic environment, provided the psychophysical tasks for judging best focus are similar. This conclusion was confirmed by a pilot study in the laboratory in the Indiana University School of Optometry that compared the effect of controlled levels of positive SA, manipulated by placing phase plates into the visual path11 on subjective refractions for small point light sources and letter charts on the same subjects. There was no difference in the impact of SA on subjective refractions for letter acuity, two-point resolution, point detection, and maximizing the perceived intensity of a bright point's core, all of which varied in a manner predicted by the VSOTF metric (by −1.4 to −2.0D per Dmm−2 of Seidel SA). These comparisons reveal that there is nothing inherent in the high contrast point source stimuli that trigger especially large myopic shifts (no greater than that seen with photopic letter charts).
However, there is one feature of retinal images generated by high contrast point sources (contrast >2000 in this study) that is unique. The tails of the PSF are low intensity, and typically go unseen on a bright background, but at nighttime very high-contrast point sources generate highly visible starbursts around small lights.16,17,33 These starbursts enlarge the overall perceived size of a spot of light, which is presumably responsible for the rather large values of two-point resolution reported in Fig. 4. Moreover, when the subjective criterion for best focus is based upon minimizing size, SA levels may have a large impact on subjective refraction as shown by Fig. 3, with slopes approaching 5 times those seen for the other refraction criteria. For example, with 0.36Dmm−2 of positive Seidel SA (Fig. 3), refractions were more than 3.25D more myopic than baseline paraxial refractive errors.
Our results suggest that if astronomers and other stargazers focus optical aids (e.g. telescopes or spectacle lenses) to remove starbursts, and if their eyes have typical levels of ocular positive SA and typical nighttime pupils, then they will observe a significant myopic shift compared to their daytime refractive errors.13,15,34 For example, without any accommodation, a subject with 0.16Dmm−2 of Seidel SA and a 7-mm pupil will experience a nighttime shift optimal refraction of −1.5D if attempting to minimize starbursts around lights. A myopic shift of −1.5D when focusing point sources in the periphery of a 6-mm pupil was also observed by Arnulf et al.35 Similarly, studies of accommodation that employed stigmatoscopy5,36 may also have measured a myopic bias with their optometers when measuring unaccommodated eyes, which would account for observations of significant accommodative leads37 reported in this literature.
The data reported here complicate the interpretation of myopic shifts in refractive state at low light levels. Although involuntary accommodation plays a significant role in the observed myopic shifts observed at scotopic light levels,31,38–40 even without accommodation, typical levels of ocular positive SA observed with large nighttime pupils can generate significant myopia if the task is to remove starbursts surrounding a high contrast point of light. These data emphasize that positive SA and pupil dilation at night may add to the impact of accommodation on night and twilight myopia, and the magnitude of the SA effect will depend upon the stimulus and the subjective criterion, being largest when subjects attempt to remove any visible starbursts. Therefore, if the ophthalmic industries are to develop night driving treatments that correct myopic shifts in spherical refractive error,41–43 a correction that optimizes nighttime visual acuity will not remove starbursts, and vice versa.17 Therefore, adding more or less negative power to a patient's habitual refraction will be less than ideal, whereas correcting their SA should be a more effective strategy.
Conflicts of interestThe authors have no conflicts of interest and have no proprietary interest in any of the materials mentioned in this article
Funding: This work was supported by the European Research Council Starting Grant ERC-2012-StG-309416 and by Fundación Séneca-Agencia de Ciencia y Tecnología de la Región de Murcia, Programa Regional “Jiménez de la Espada”, grant number 20118/EE/17 to NL-G.