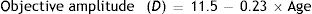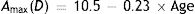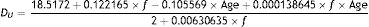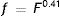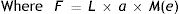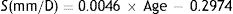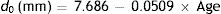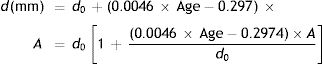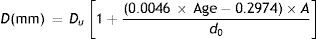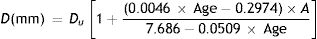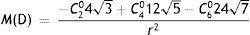To develop a flexible model of the average eye that incorporates changes with age and accommodation in all optical parameters, including entrance pupil diameter, under photopic, natural, environmental conditions.
MethodsWe collated retrospective in vivo measurements of all optical parameters, including entrance pupil diameter. Ray-tracing was used to calculate the wavefront aberrations of the eye model as a function of age, stimulus vergence and pupil diameter. These aberrations were used to calculate objective refraction using paraxial curvature matching. This was also done for several stimulus positions to calculate the accommodation response/stimulus curve.
ResultsThe model predicts a hyperopic change in distance refraction as the eye ages (+0.22D every 10 years) between 20 and 65 years. The slope of the accommodation response/stimulus curve was 0.72 for a 25 years-old subject, with little change between 20 and 45 years. A trend to a more negative value of primary spherical aberration as the eye accommodates is predicted for all ages (20–50 years). When accommodation is relaxed, a slight increase in primary spherical aberration (0.008μm every 10 years) between 20 and 65 years is predicted, for an age-dependent entrance pupil diameter ranging between 3.58mm (20 years) and 3.05mm (65 years). Results match reasonably well with studies performed in real eyes, except that spherical aberration is systematically slightly negative as compared with the practical data.
ConclusionsThe proposed eye model is able to predict changes in objective refraction and accommodation response. It has the potential to be a useful design and testing tool for devices (e.g. intraocular lenses or contact lenses) designed to correct the eye's optical errors.
Desarrollar un modelo flexible de ojo medio que incorpore los cambios en función de la edad y la acomodación en todos los parámetros ópticos, incluyendo el diámetro de pupila de entrada, en condiciones ambientales fotópicas y naturales.
MétodosRecopilamos medidas retrospectivas in vivo de todos los parámetros ópticos, incluyendo el diámetro de pupila de entrada. Se usó un trazado de rayos para calcular las aberraciones de frente de onda del modelo ocular en función de la edad, vergencia de estímulo y diámetro de la pupila. Se utilizaron dichas aberraciones para calcular la refracción objetiva mediante el criterio de curvatura paraxial. Esto se realizó también para diversas posiciones del estímulo, para calcular la curva de respuesta acomodativa.
ResultadosEl modelo predice un cambio hipermetrópico en la refracción de lejos a medida que el ojo envejece (+0,22 D cada 10 años) entre los 20 y los 65 años. La pendiente de la curva de respuesta acomodativa fue de 0,72 para un sujeto de 25 años, con pocos cambios entre los 20 y los 45 años. Se predice una tendencia hacia un valor más negativo de la aberración esférica primaria a medida que el ojo acomoda, en todas las edades (de 20 a 50 años). Con la acomodación relajada, se predice un ligero incremento de la aberración esférica primaria (0,008μm cada 10 años) entre los 20 y los 65 años, para un diámetro de pupila de entrada dependiente de la edad que oscila entre 3,58mm (20 años) y 3,05mm (65 años). Los resultados concuerdan razonablemente bien con los estudios realizados en ojos reales, exceptuando que la aberración esférica es ligera y sistemáticamente menor en comparación a los datos experimentales.
ConclusionesEl modelo de ojo propuesto es capaz de predecir los cambios de la refracción objetiva y la respuesta acomodativa. Tiene el potencial de ser una herramienta útil de diseño y prueba de elementos correctores (e.j.: lentes intraoculares o lentes de contacto) de los errores ópticos del ojo.
Numerous eye models have been developed in attempts to help us to understand the formation and characteristics of the retinal image, in both emmetropic and ametropic eyes, with or without an optical correction.1,2
One of the most famous eye models is Gullstrand's “No. 1” or “exact” eye.3 This model has a crystalline lens with a nucleus and cortex having different refractive indices. It is specified in two different accommodative states (0 and 4D). Gullstrand's eye model is a good approximation to a real eye. However, at the time that it was introduced, it proved to be too complicated for many purposes. Thus later authors4,5 developed new, simplified, eye models to make calculations easier to perform. In contrast, with the availability of computers to speed calculation, other more recent models have often included additional characteristics in order to achieve a better approximation to real eyes, such as: aspheric surfaces6–12; chromatic dispersion6,9,12; intraocular scattering13; changes with accommodation3,4,6,9,11,12,14; and age.7,11,15,16 In the last few years, information produced by new devices capable of taking numerous “in vivo” clinical measurements of the optical parameters of real eyes has been used by some authors to develop further eye models based on statistical data for the ocular parameters.11,12,17–19
Although some “in vivo” measurements of the internal GRIN distribution of the crystalline lens and its changes with age and accommodation have been made,20–22 these direct data are still too limited in the ranges of age and accommodation covered to be modelled exactly. This has led several authors to model the crystalline lens either as a GRIN lens with assumed index distributions characterised by several variable parameters which are optimised to produce lens characteristics thought to approximate to those of the real lens,7,8,12,14,23–25 or as a homogeneous lens with an equivalent refractive index (ERI) that simulates the optical performance of the human GRIN lens.26–29 The variability between individuals has led some authors to develop personalised eye models to reproduce optical performance of the eye from optical measurements of each subject. Among the goals of these studies has been the modelling of the GRIN crystalline lens17 and the retinal contour.30
While these models have proved to be useful, most suffer from the limitation of either being paraxial or of using a fixed pupil size. Under natural conditions, the pupil diameter varies with a variety of factors, including illumination, age and accommodation. As far as we know, only one study19 has included data for natural scotopic pupil size and none of the existing models includes changes in pupil size with accommodation and age. Pupil diameter affects wavefront aberration and ocular depth-of-focus, as well as the light flux reaching the retina. Although studies suggest that subjective distance refraction does not change much with pupil size variation in photopic conditions,31,32 if the pupil diameter changes, variations in non-paraxial accommodation response to a fixed stimulus may occur as a result of changes in wavefront aberration, even if the crystalline lens geometry remains the same.33
The purpose of the present study is to develop a simple eye model, based on earlier work by Dubbelman et al.28,34–37 and Norrby.11 This is intended to be able to predict the “typical” eye's spherical aberration, refraction and accommodation response in natural conditions, particularly as a function of the accommodation stimulus and age. In order to achieve this goal, we have used retrospective “in vivo” measurements of all ocular parameters (Table 1). The model also includes photopic natural pupil size and its changes with accommodation and age. It is presented as a table of equations with age and accommodation demand as variables. The model is validated by comparing its predictions of changes with age in spherical aberration, refraction, and accommodation and with the results of studies performed in real eyes. Suggestions are made for improvements and applications of the model.
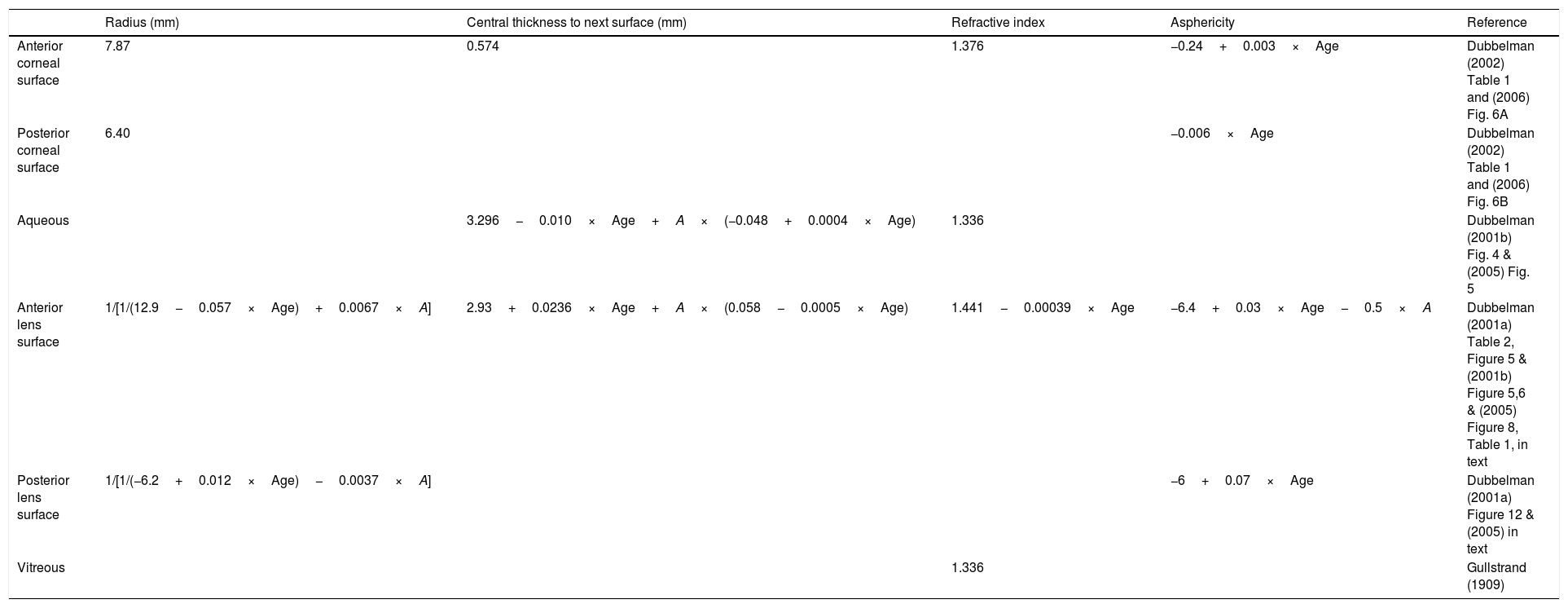
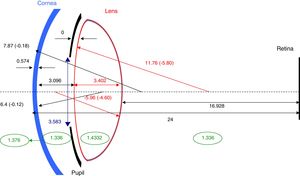
Model parameters. Summary of data extracted from Dubbelman et al.’s studies. Variables are age (years) and accommodative stimulus (A, diopters). Refractive indices of cornea, aqueous and vitreous extracted from Gullstrand (1909).
| Radius (mm) | Central thickness to next surface (mm) | Refractive index | Asphericity | Reference | |
|---|---|---|---|---|---|
| Anterior corneal surface | 7.87 | 0.574 | 1.376 | −0.24+0.003×Age | Dubbelman (2002) Table 1 and (2006) Fig. 6A |
| Posterior corneal surface | 6.40 | −0.006×Age | Dubbelman (2002) Table 1 and (2006) Fig. 6B | ||
| Aqueous | 3.296−0.010×Age+A×(−0.048+0.0004×Age) | 1.336 | Dubbelman (2001b) Fig. 4 & (2005) Fig. 5 | ||
| Anterior lens surface | 1/[1/(12.9−0.057×Age)+0.0067×A] | 2.93+0.0236×Age+A×(0.058−0.0005×Age) | 1.441−0.00039×Age | −6.4+0.03×Age−0.5×A | Dubbelman (2001a) Table 2, Figure 5 & (2001b) Figure 5,6 & (2005) Figure 8, Table 1, in text |
| Posterior lens surface | 1/[1/(−6.2+0.012×Age)−0.0037×A] | −6+0.07×Age | Dubbelman (2001a) Figure 12 & (2005) in text | ||
| Vitreous | 1.336 | Gullstrand (1909) |
The basic model resembles many previous models in using four optical surfaces and a homogeneous lens. Its novel feature is that all of its biometric parameters may, as appropriate, change as a result of age and accommodation. Further, the diameter of the model's entrance pupil also changes systematically in response to the stimulus conditions and the age of the individual.
Surface radii and asphericities, distances, and refractive indicesIn order to ensure that the input parameters of the model were self-consistent, all values were extracted from the “in vivo” measurements of Dubbelman and collaborators.28,34–37 Their measurements were made on groups between 65 and 114 subjects, using a Scheimpflug Nidek Eas-1000 camera (Nidek Co Ltd, Japan). The Scheimpflug images were corrected for distortions produced by device geometry and corneal reflection. The original authors fitted their measured parameters by equations in which age and accommodation stimulus were included as variables. A summary of these equations can be found in Table 1. Conicity data were converted into Zemax OpticStudio (Zemax LLC, WA, USA) convention.
Refraction can be very variable between subjects, and is highly influenced by axial length. As our model tries to achieve an average refraction, we assume a constant axial length of 24mm.38–40 However, this parameter can be changed as required, for example, in order to study changes in wavefront and refraction in other conditions. No curvature is added to the retina, as at present only axial optical performance is modelled.
In order to further simplify calculations, the eye model is chosen to be rotationally symmetric (and hence free of asymmetric aberrations) and, in view of the current uncertainties about the index gradients in the lens, assumes a single age-dependent, equivalent refractive index for the lens.28
Since the amplitude of accommodation falls with age, with the objective amplitude typically reaching zero at an age of about 50 years, the equations in Table 1 which involve accommodation will only be valid over a limited range of ages and accommodation stimuli. The original data of Dubbelman and his collaborators were derived from subjects aged 16 to 65. However, when fitting regression equations including the accommodation stimulus, A, as a variable, they used data only from subjects aged between 16 to 52 years.35 We assume that the model will apply over the more conservative range of 20–50 years, since within this range, the objective amplitude of accommodation falls approximately linearly.41–45 Below 20 years, the change in objective amplitude with age becomes non-linear and above 50 years accommodation is usually inactive. We further assume that the amplitude falls from a value of about 7D at the age of 20 to zero at the age of 50.44–46 The typical objective amplitude can therefore be approximated by
In practice there are, of course some inter-subject variations in the values of these parameters.41,43 This, however, is the full objective amplitude and our regression equations effectively assume that accommodation response is linearly dependent on the accommodation stimulus within this amplitude range. In practice this is only true for the lower part of the typical accommodation response/stimulus curve. The upper part of the curve becomes non-linear, with response saturation occurring when the full objective amplitude is exerted.47 We approximate the range within which the response is non-linear as 1D, so that age range within which the equations are applicable is reduced to about 20–45 years. Since the objective amplitude refers to maximum accommodation response, the corresponding stimulus value depends upon the slope of the response/stimulus function. For our present purposes we make the conservative assumption that the slope is unity, so that the upper limit of accommodation stimulus, A, for which the regression equations of Table 1 are valid, Amax, is approximated by:
These restrictions only apply when A is non-zero. For the case when A=0, the equations of Table 1 should all be valid over the full 20–65 year age range of the Dubbelman et al.,35 data.
Note that although it is assumed in Table 1 that the lens characteristics change with age and accommodation stimulus, the pupil diameter is not included in the relevant equations. Thus, at any age, the geometric form of the accommodated lens at any particular stimulus level, A, is independent of pupil diameter. This assumption is likely to be broadly valid at photopic luminances with natural pupil diameters in the range of 3–5mm, where the characteristics of the accommodation response/stimulus curve show little change with luminance level and the associated pupil diameter, but is not true at mesopic and scotopic light levels when the natural pupil is large and the slope of response/stimulus curve falls progressively as the luminance falls.48–50 It is also not applicable at photopic luminance levels when small artificial pupils (<3mm) are used51 and accommodative lags again become large due to the enhanced ocular depth-of-focus.
Entrance pupil diametersAn initial estimate of pupil size with relaxed accommodation under specified stimulus conditions was extracted from Watson and Yellott's analysis,52 in which they collated data from previous pupil studies and fitted them by a unified formula for light-adapted pupil size:
where DU denotes entrance pupil diameter in mm, Age is subject's age in years and f is a term defined as the effective corneal flux density (F) raised to the power 0.41, i.e.:
“L” and “a” are the luminance (cdm−2) and area (deg2) of the adaptation field. “M(e)” is a monocular/binocular factor in which “e” is the number of eyes observing the stimulus, and M(1)=0.1 (monocular) and M(2)=1.0 (binocular).
Watson and Yellott52 state that these formulae are valid for subjects older than 20 years of age without restriction on the adaptation field. We have accepted this but note that, at the present time, the pupil dependence on “a” has only been experimentally confirmed for field sizes up to about 500 deg2.53
While Watson & Yellott's formulae give the pupil diameter, DU, with relaxed accommodation, it is well known that, in general, the pupil diameter reduces as accommodation increases (accommodative miosis). To quantify this effect in the model, appropriate data were taken from López-Gil et al.’s54 study, in which the eyes of 60 subjects with different ages (from 19 to 60 years old) were measured for several accommodative stimulus levels (0–5D, with 1D steps). López-Gil et al. give regression equations for different age groups for the changes in the pupil diameter from its relaxed-accommodation value as a function of the accommodation response. These slopes from these equations were transformed to slopes, S mm/D, for the plots of pupil diameter as a function of accommodative stimulus, using response/stimulus data provided by the authors. It was found that S as function of age could be described by the regression equation
where the age is in years. The magnitude of the miosis for any given stimulus value reduces with age.The pupil diameters, d0 mm, with relaxed accommodation (A=0, where A is the accommodation stimulus, taken as positive, in dioptres) in López-Gil et al.’s54 study could be fitted with the regression equation:
Thus the pupil diameter, d mm at any age and stimulus level in the López-Gil study is given by:
If the “relaxed” pupil diameter at any age has a value Du mm, rather than the d0 applying in the López-Gil54 study, we assume that the pupil diameter as a function of age and accommodation will scale accordingly, by the factor Du/d0, i.e.
and, introducing Eq. (7)
Calculation of refraction, accommodation response and spherical aberrationRay-tracing software (Zemax Optic Studio, Zemax, WA, USA) was used to calculate the wavefront aberrations of the eye model for different specified combinations of age, stimulus vergence, and pupil diameter, using the biometric parameters as given in Table 1 and the pupil diameters, DU, given by Watson and Yellott's equations and Eq. (9). The Zernike coefficients of the wavefronts up to the sixth radial order were calculated for a wavelength of 555nm. Since the model is symmetrical about the axis, the only non-zero coefficients were C20, C40, C60, i.e. defocus, primary spherical aberration and secondary spherical aberration.
These aberration coefficients were used to calculate the spherical equivalent objective refraction, M(D), using paraxial curvature matching,55 where
Cnm (microns) denotes the Zernike coefficient of radial order n and azimuthal frequency m, and r (mm) is the entrance pupil radius. Thibos et al.,55 found that the paraxial curvature method gave results for equivalent spherical error which accorded well with those of subjective refraction. Other criteria, such as least-squares fitting with a quadratic surface (minRMS), could be used to estimate refraction from the modelled wave aberration if required.
The astigmatic J0 and J45 power vectors55 were not calculated, since our model assumes rotational symmetry about the optical axis and data extracted from Dubbelman and collaborators’ studies were averaged to a spherical equivalent.
For the accommodative response calculations, the spherical equivalent refraction of the eye model was calculated for stimulus positions at 0.5D intervals over the accommodation range of the age group concerned, using accommodation-stimulus dependent lens and ACD parameters derived from the equations of Table 1.
As noted above, the Zernike fourth-order spherical aberration coefficients, C04 microns, of the model for any combination of conditions and age were calculated directly using Zemax software. Since pupil diameter changes with the observing conditions and age, it is sometimes helpful to compare spherical aberration across conditions in terms of its dioptric changes with zonal radius, i.e. in terms of D/mm2. This can be derived from the Zernike coefficient using
where r is the pupil radius (mm) and C40 is the corresponding 4th-order spherical aberration Zernike coefficient in microns.56 Expressed in this terms the longitudinal spherical aberration in diopters for a marginal ray of a pupil of radius r (in mm) is simply: Longitudinal spherical aberration (D/mm2)×r2.As noted earlier, the proposed model is intended to be valid for an age range between 20 and 65 years for predictions with relaxed accommodation and between 20 and 45 years for predictions with active accommodation.
Validation of the modelTo validate the model, its predictions were compared with experimental data from the literature. The following photopic observation conditions were assumed for the modelling:
- -
Adaptation field luminance (L): 40cd/m2.
- -
Adaptation field area (a): 15100deg2.
- -
Number of eyes (e): 1 (monocular).
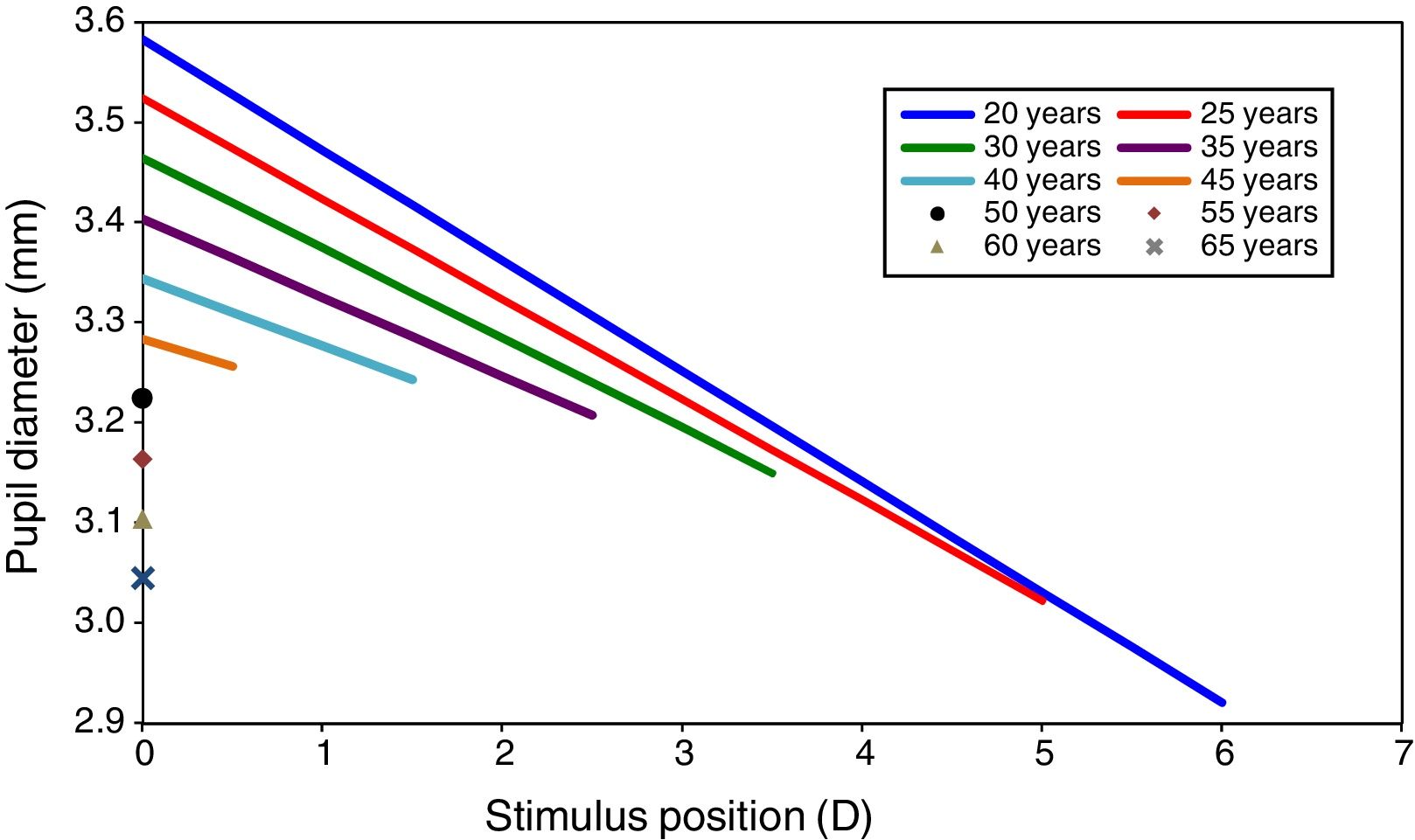
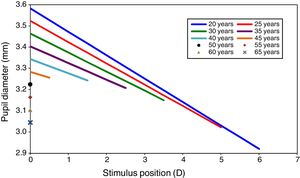
The field area assumes that the full monocular visual field is illuminated. Insertion of these values in Watson and Yellott's formulae for pupil diameter with relaxed accommodation gave a pupil size, Du, ranging between 3.6mm and 3.0mm as the age changed from 20 to 65, (see Fig. 1 for stimulus position 0D). These limits correspond well to measurements of entrance pupil size made under photopic conditions with a wide illuminated field.57,58 The values of pupil diameter are smaller than those found experimentally by Winn et al.,59 primarily because the latter only used a small adapting field (5 deg radius or about 80deg2) as compared to the much larger field assumed for illustrative purposes in the present work.
Pupil size as a function of accommodation stimulus position for different ages. Data extracted from Watson et al. and Lopez-Gil et al.’s studies. Graphs show the pupil size for only the accommodation stimulus range over which accommodation response/stimulus curve is approximately linear, but not the whole change in pupil size for each age.
Allowance was then made for the effects of accommodative miosis over the age-dependent stimulus range within which the accommodation system is still active, using Eq. (9). The resulting predicted pupil diameters at various ages are shown in Fig. 1.
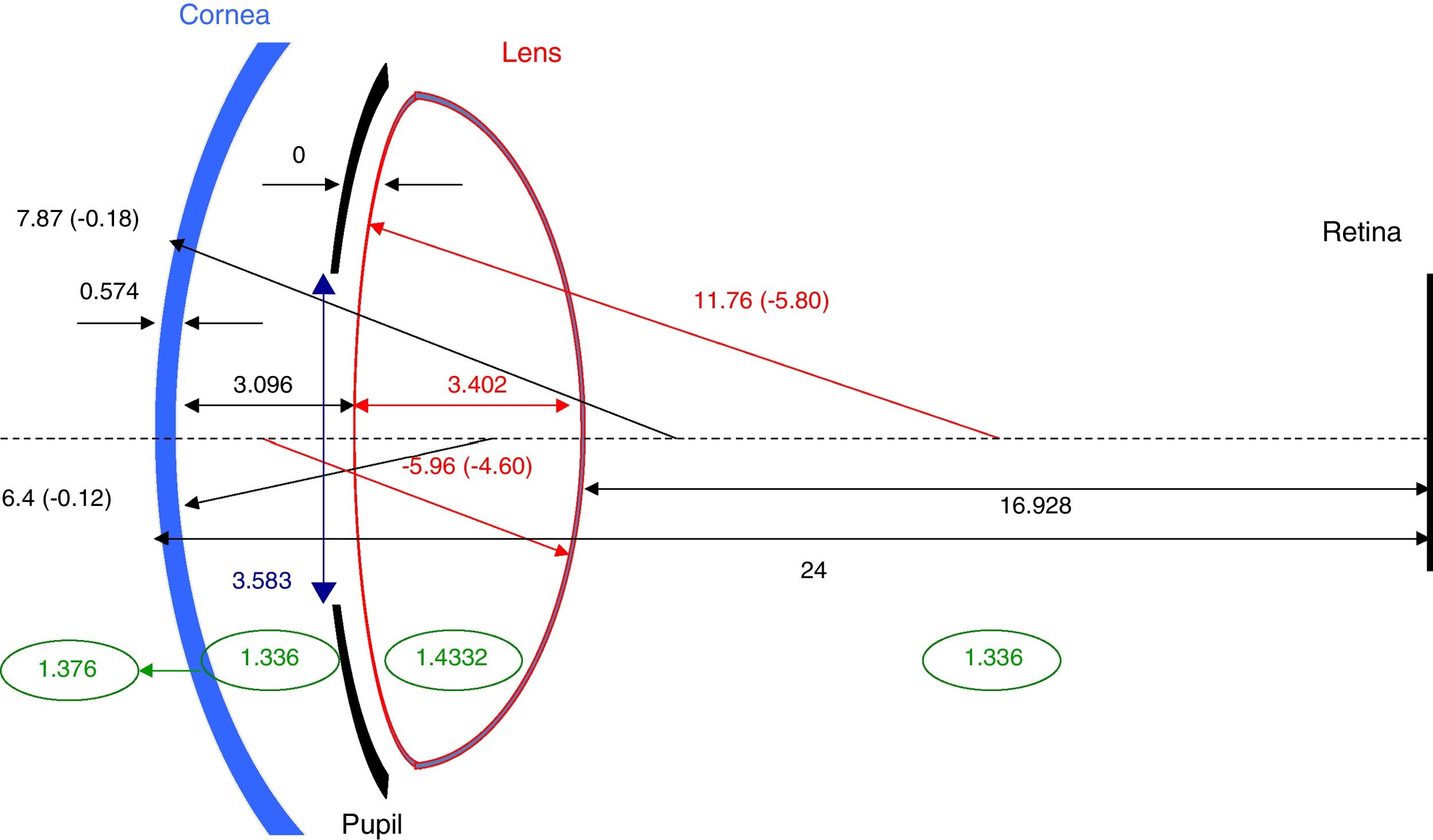
Thus the full model for these observing conditions consists of a series of individual eye models, each characterised by the age of the subject and the accommodation stimulus. Fig. 2 gives an example of the overall model parameters for one combination of subject and conditions (20 year-old subject, accommodation stimulus A=0).
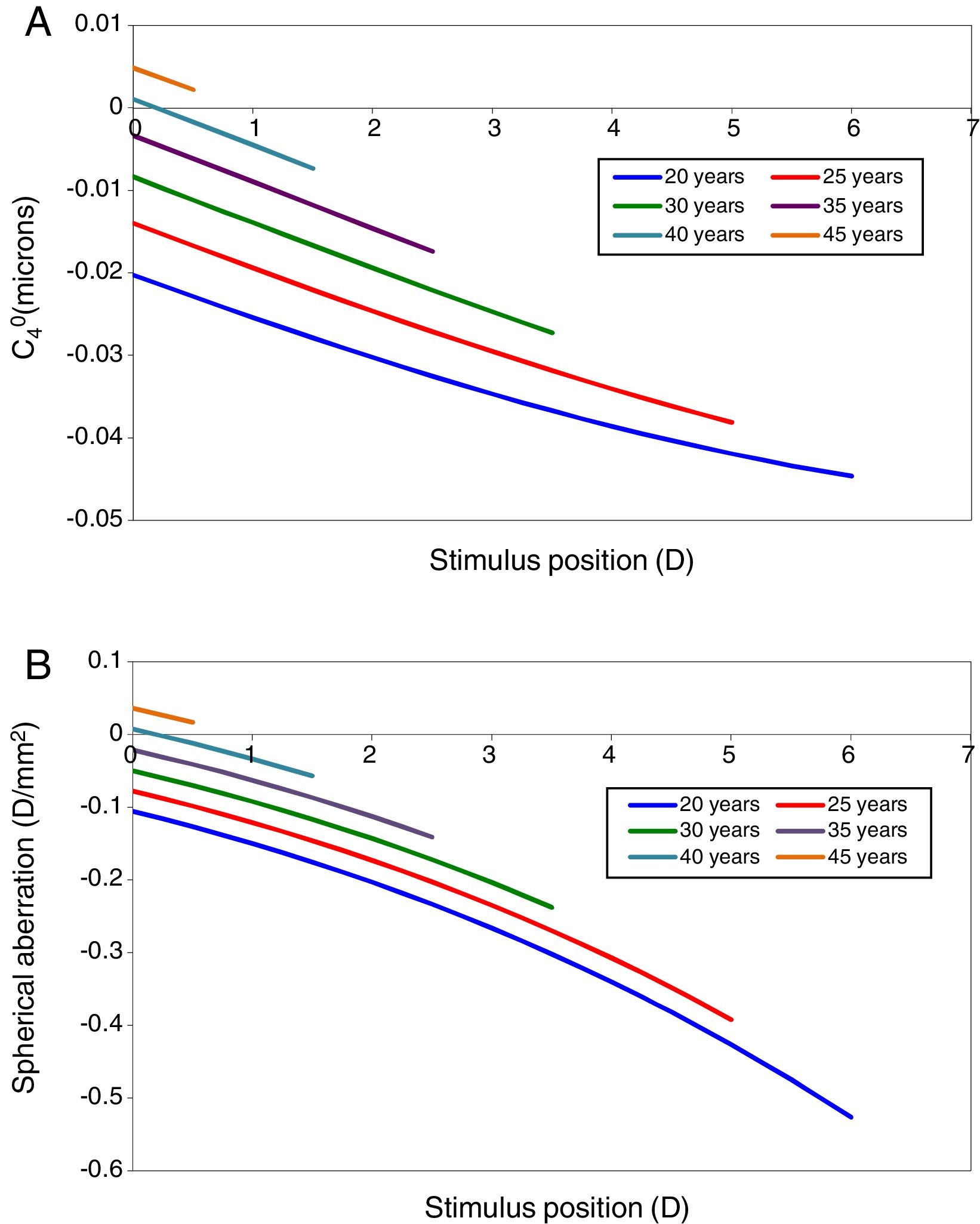
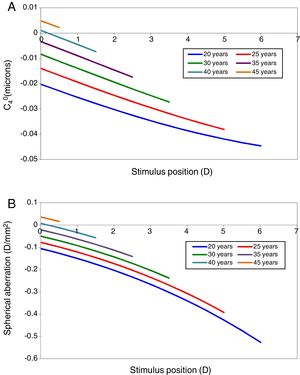
Results of modellingSpherical aberrationSpherical aberration is considered first, since its value influences the refraction and accommodation response as estimated by paraxial curvature matching. The model's predictions of the changes in primary spherical aberration with accommodation at different ages are shown in Fig. 3. Fig. 3A shows the changes in C40 in microns for the appropriate natural pupil diameter at different ages (see Fig. 1) and Fig. 3B the same changes expressed in D/mm2, so that the results can be compared at constant pupil diameter to allow the contribution of the pupil miosis to be assessed. Older eyes have more positive values of spherical aberration than younger eyes. A change in the negative direction in spherical aberration with accommodation can be appreciated for all ages from 20 to 45 years old.33,60,61 Note, however, that the values of the coefficients are small (<1/10 wavelength) for the pupil diameters (about 3mm, see Fig. 1) under consideration, so that the associated effect on image quality and paraxial focus will also be small.
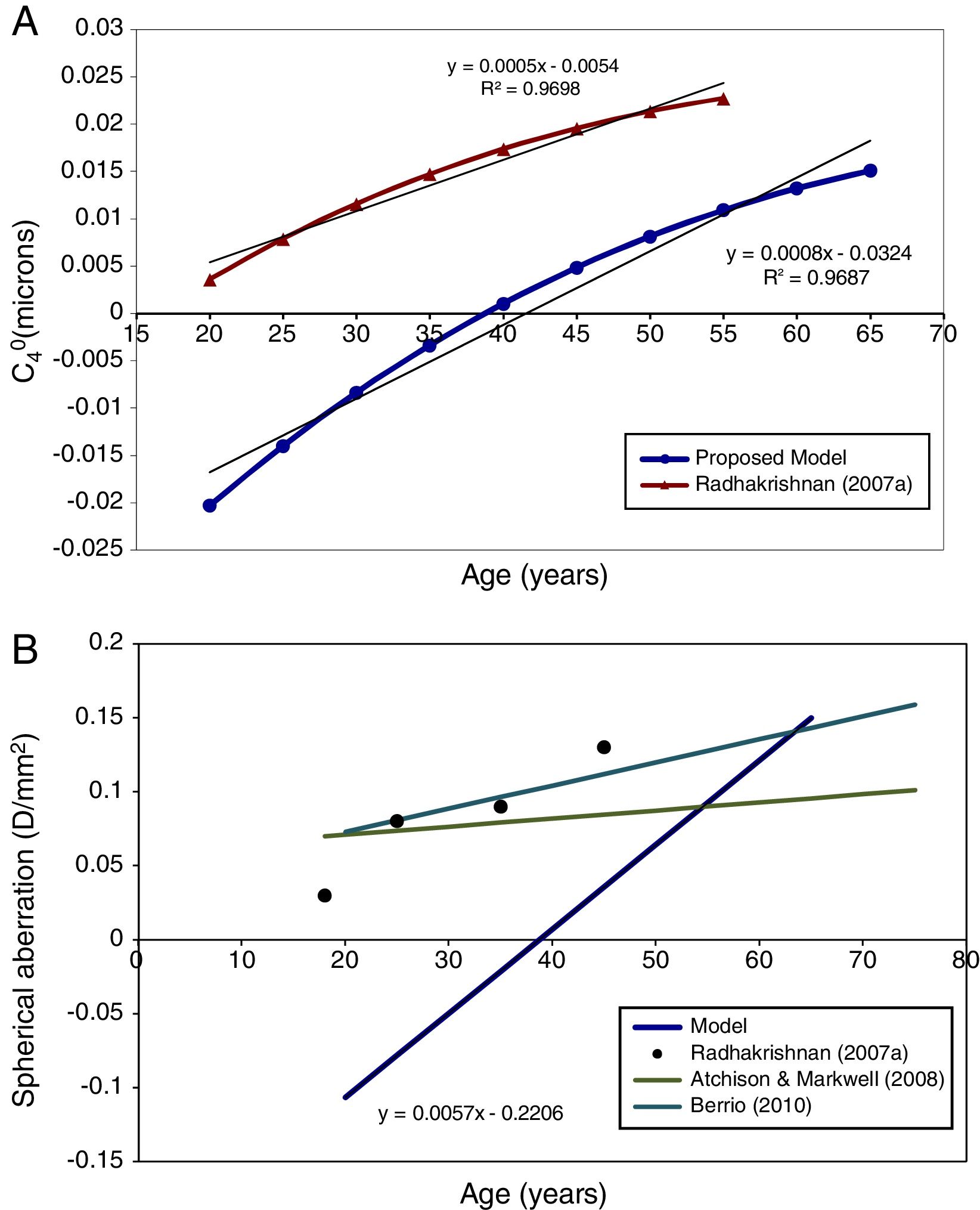
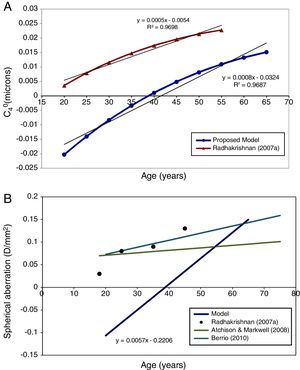
In Fig. 4 the model's results are shown for the unaccommodated eye as a function of age. Fig. 4A shows the value of C40 in microns for the natural pupil as function of age and also includes for comparison mean experimental measurements from Radhakrishnan and Charman.56 The latter results were scaled to the pupil sizes included in this model. C40 at natural pupil diameter becomes more positive with increasing age.
This trend with age still stands when the fourth-order spherical aberration is expressed in D/mm2. Fig. 4B shows the regression line for the model results, and for experimental data, also expressed in D/mm2.56,62,63 It can be seen that the agreement in general trends with age between model and Radhakrishnan and Charman's56 experiment is reasonable, particularly considering the large inter-subject variability in values found in the experimental studies, but that the model values are systematically more negative than the measured values. Atchison and Markwell62 and Berrio et al.,63 found a smaller change with age (Fig. 4B).
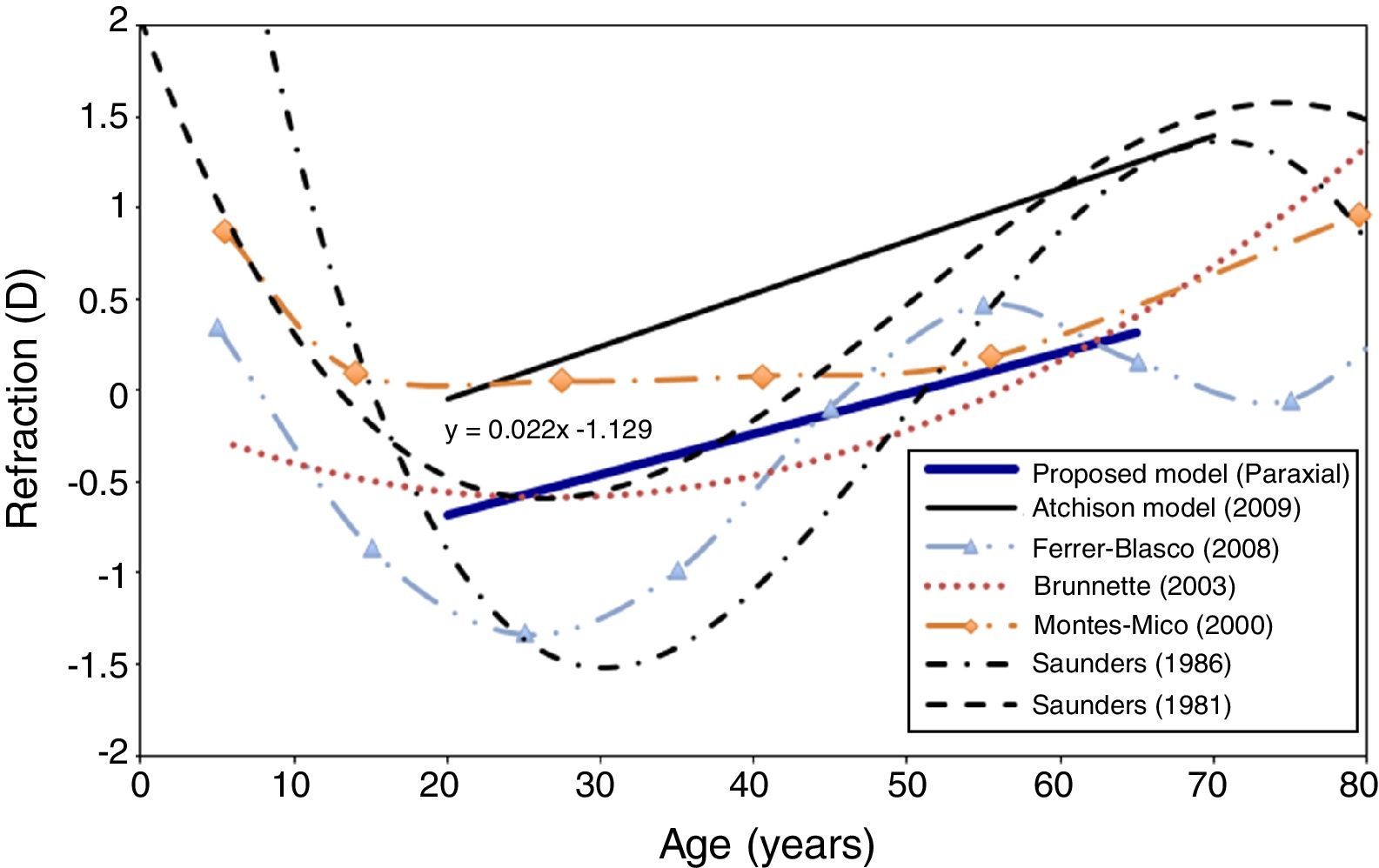
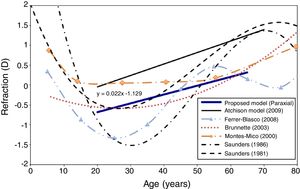
RefractionFig. 5 shows the change in objective refraction (for the unaccommodated eye) with age, as calculated from the wavefront of the eye model using the paraxial curvature matching method.55 The figure shows a trend to a more hyperopic state as the eye ages through adulthood. With the current assumptions, the eye model achieves an emmetropic state at around 50 years of age and shows a 0.22D change in refraction towards hyperopia every 10 years. Another model15 and experimental results for the age dependency of spherical refraction from other studies are shown for comparison.
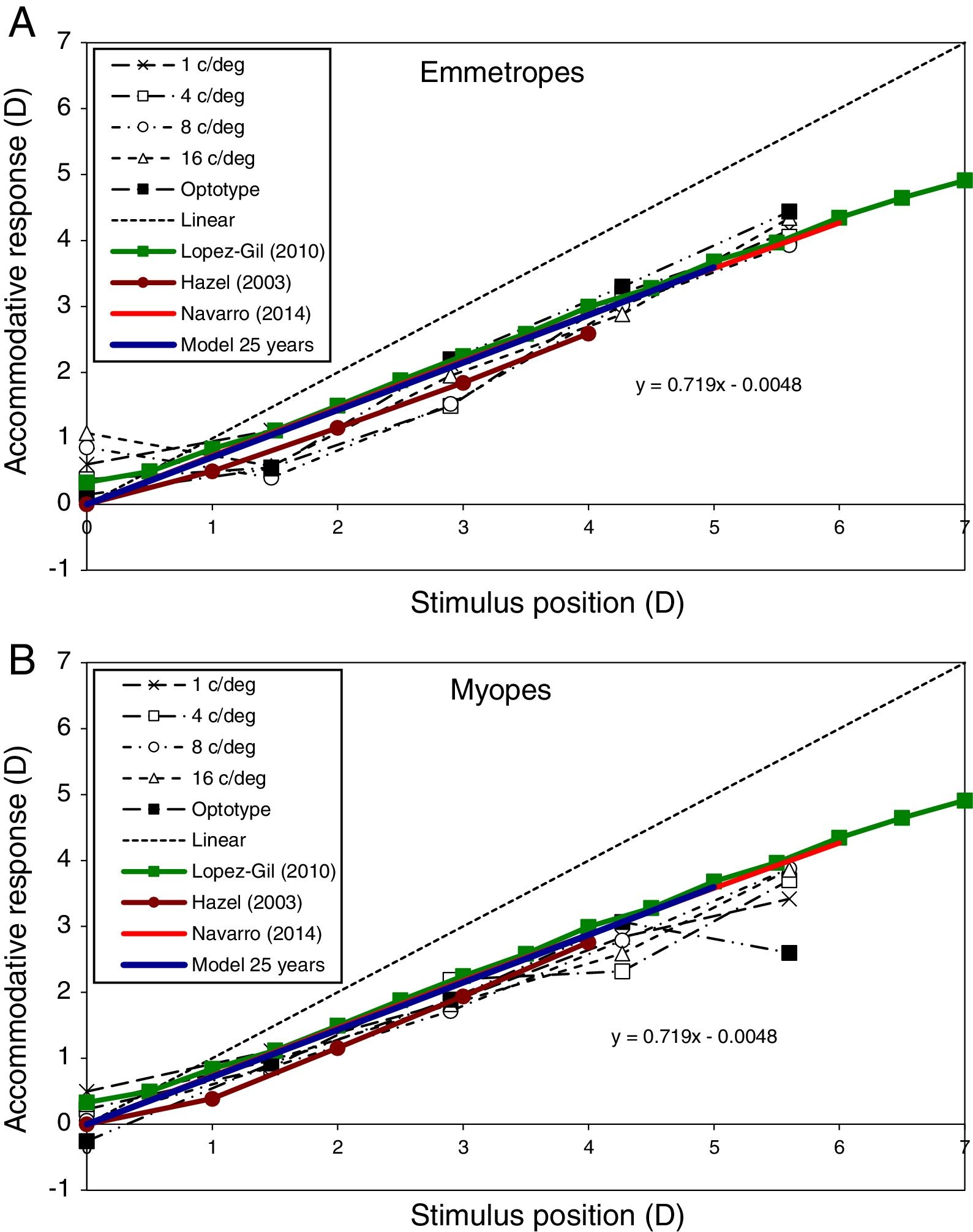
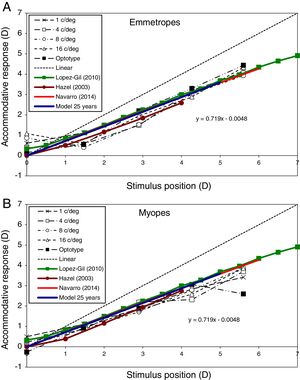
Accommodative responseFig. 6 shows the modelled accommodative response/stimulus curve for the specific case of a 25 year-old subject and the one presented by Navarro12 based on a different model and method of determining the refraction. The method used by Navarro to calculate refraction was the minimum root mean square size of the spot diagram. In this figure, both models assumed that the far point of the eye (0D of accommodative response) lay at infinity (i.e. 0D stimulus). The best linear fitting for the proposed example is y=0.72x+0.01, compared with y=0.71x+0.03 for the Navarro eye model. This figure also shows experimental results extracted from López-Gil et al.,64 Hazel et al.,65 and Taylor et al.,66 for comparison. Some of these studies65,66 divided their results into refractive groups (e.g. emmetropes and myopes), so we represent emmetropes in Fig. 6A and myopes in Fig. 6B. López-Gil et al.,64 averaged results of emmetropes and myopes without distinction, thus we plot their results in both graphs for comparison.
Accommodative response predicted by the proposed model (blue line) for the 25-year-old case. Comparisons with Navarro (2014) model (red line) and experimental results of an emmetropic subject (Subject A, above) and a myopic subject (Subject C, bottom) extracted from Taylor et al. (2009) for several spatial frequencies (black lines). López-Gil (2010, green line) and Hazel (2003, brown line) experimental results are also shown in both graphs for comparison. Linear (dashed line) represents ideal response.
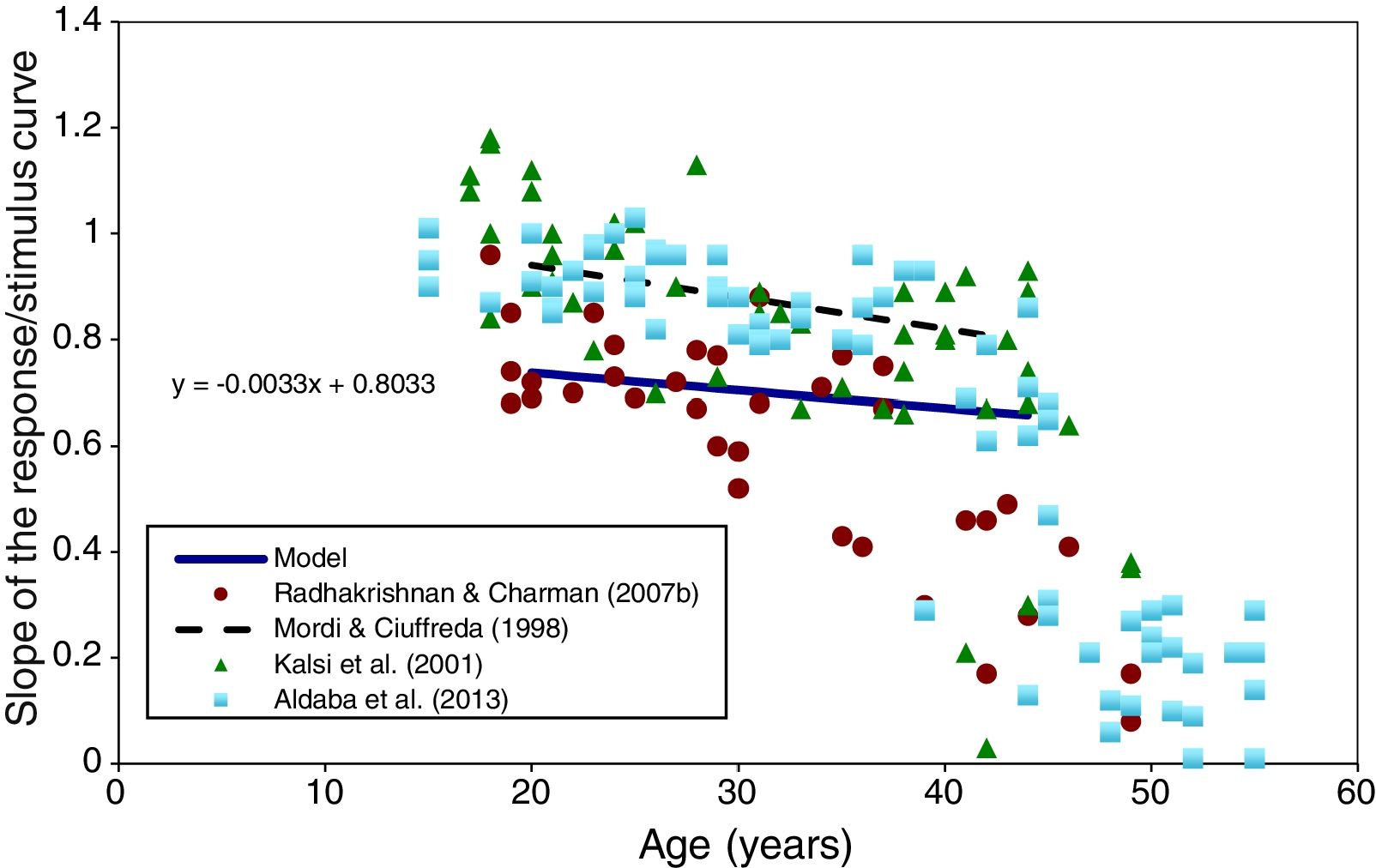
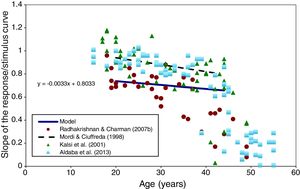
The modelled change in the slope of the response/stimulus curve with age is shown in Fig. 7. This shows a slight decrease in response/stimulus slope as age increases over the range 20–45. The results obtained in several experimental studies46,67–69 are shown for comparison and appear to be broadly similar.
Slope of the accommodation response/stimulus curve as a function of age (between 20 and 45 years) predicted by the model (full black line). Experimental results extracted from Radhakrishnan and Charman,67 Kalsi et al.,69 Mordi and Ciuffreda,70 and Aldaba et al.,46 are shown for comparison.
The proposed model is based on retrospective data extracted from several studies.28,34–37,52,54 Most of the data were collated in a previous work by Norrby,11 but our proposal is an upgrade of his earlier model. It includes some changes such as corneal and lens asphericities and their changes with age, and the addition of the pupil size model including changes with age and accommodation.
The biometric data28,34–37 on which the model is based were obtained under conditions in which subjects accommodated monocularly on a Maltese-cross target under photopic conditions. Accommodation was stimulated with lenses. Strictly speaking, then, the model should be restricted to these conditions. However, in practice the photopic accommodation response/stimulus curve shows only minor changes with target form,66,71 monocular/binocular viewing72,73 or variations in photopic target luminance,50 so that it is reasonable to compare the model's predictions with experimental data obtained under broadly similar, but not necessarily identical, conditions.
Results in this work have been calculated for a natural pupil under specific, representative, photopic conditions for the unaccommodated eye. Nevertheless, one of the advantages of this model is that these conditions can be changed in order to study other situations with different conditions of luminance and visual field (Eqs. (3)–(5)), which will give a different value of pupil diameter for the unaccommodated eye. Once this value is fixed, it can be used Eq. (9) to calculate the pupil diameter for a certain stimulus vergence and age.
It is worth noting that most of the results show a purely linear trend. This is due to the fitting of most of the model's parameters with linear equations, an exception being the case of the change in the pupil size with age.
Predictions extracted from this work were: changes produced in primary (4th-order) spherical aberration (C40) with accommodation and age; refractive change produced in adult human eye with age; and accommodative response and its changes with age. Do the model's predictions show reasonable agreement with experimental data obtained under conditions comparable to those assumed in the model?
With respect to primary spherical aberration, Fig. 3A shows that C40 becomes less positive with increasing accommodation,33,60,61,74 in agreement with other studies which take into account accommodative miosis. Fig. 3B shows that the same basic trend with accommodation towards more negative values of spherical aberration still remains when the aberration is expressed in terms of D/mm2 to avoid the influence of pupil miosis on C40.
Fig. 4A shows a slight positive increase in the value of C40 as the unaccommodated eye gets older, as generally found in practical studies.56,62,63,75–77Fig. 4B shows that this trend still stands when the effect of pupil miosis is minimised by expressing the results in terms of D/mm2. This increase in total C40 with age is produced by a decrease in the internal compensation of the corneal C40 by the C40 of the lens,78 mainly produced by the change in lens asphericity with age.79
However it is clear that the values of spherical aberration produced by the model are systematically too negative with comparison with the experimental data. We tentatively attribute this to the values of surface conicity used in the model, particularly that of the posterior surface of the lens. A similar conclusion was reached by Norrby11 when discussing the results produced with his own model based on the Dubbelman et al. data. Atchison18 has pointed out the possible effects cumulative errors on estimates of the radius and conicity of the posterior surface of the lens when tracing back through the eye in the Scheimpflug technique and Smith et al.,80 have further elaborated on the inadequacies and inconsistencies of experimental determinations of lens asphericities. Another possible reason might be the inability of the lens equivalent refraction index to simulate the changes in the lens GRIN distribution with accommodation.81
A trend to a more hyperopic state as the eye gets older can be seen in Fig. 5. This tendency is in agreement with numerous studies performed in real eyes.76,82–85 The model's predicted hyperopic change in refraction between 20 and 65 years of age is 1.0D. This value is very close to those obtained by Brunette et al.,76 Ferrer-Blasco et al.,83 and Saunders84 in studies performed in large populations. The model produced linear change in refraction between 20 and 50 and failed to predict the myopic trend apparent up to the age of about 30 in many practical studies. It may be that the latter is a selection effect in that much of the data is obtained in a clinical context, where younger emmetropes and hyperopes fail to present themselves for examination, in contrast to the older population who are well represented since all need a near correction.
The main feature of the proposed eye model is the prediction of the static accommodative response of the eye and its changes with age. As far as we know, only one previous eye model12 has shown a good prediction which matches with real measurements of accommodative response of young subjects (age 25). The current model improves this prediction further by extending predictions to the age of 45 and by considering that pupil size and hence optical performance will change with age and accommodation, instead of using a fixed pupil.
The accommodative response predicted by the model for young adults (age 25) (Fig. 6) reasonably matches the results of other studies performed in real eyes.64–66 In the case of emmetropic subjects (Fig. 6A), the proposed model matches shows a slightly smaller accommodative lag than the results of Hazel et al.65 In the case of myopic subjects (Fig. 6B), the proposed model predicts the results of all the 3 studies very well.
The change in response/stimulus slope with age, shown in Fig. 6, suggests a slight increase in the accommodative errors as the eye gets older. Up to the age of about 40, this is reasonable agreement with studies performed in real eyes.67 However, all the experimental studies found a larger decrease in the slope of the accommodation response for subjects older than about 40 years, with most individuals having lost all objective accommodation by the age of 50. This emphasises the need to restrict the application of the accommodation aspects of our model to ages below about 45 years.
Eye models are useful tools to aid the design of optical corrections such as contact or intraocular lenses, since the wavefront and the power of the eye need to be correctly specified in order to find the best correction possible. As pupil size influences wavefront aberrations, depth-of-focus and accommodative response,86 changes in pupil size with age and accommodation are important factors in the design of new corrections, such as aspheric lenses to compensate for the spherical aberration of the eye or lenses with extended depth-of-focus. At present, eye models with fixed pupil sizes are usually used to design aspheric lenses which try to correct the spherical aberration of the eye,87 even though the optical performance of most multifocal contact and intraocular lenses is pupil-dependent. Allowance for the natural pupil size of the eye and its changes with age and accommodation could improve these designs in order to achieve a better image quality and to take advantage of ocular miosis to extend depth-of-focus.
All the assumptions in the present model were made in order to get the simplest model able to achieve the predictions pursued in this study. This model is currently not able to predict non-rotationally symmetric aberrations, astigmatism, and peripheral refraction. The exclusion of asymmetric aberrations is a particular disadvantage, in that coma is usually the most important aberration affecting foveal vision. This means that, at present, calculations of axial image quality based on the model are of limited utility. The limitations could be assessed in future work involving, e.g., the inclusion of typical lens tilt and foveal decentration, or the effects of chromatic aberration. While other eye models12,23,24 have used optimisation of some parameters to produce results which better match experimental evidence, the present model has been designed by using in vivo retrospective measurements without adding any optimisation. In an attempt to ensure that a self-consistent set of input parameters was used, all the parameters are taken from the Scheimpflug studies of Dubbelman and his collaborators and it may be that parameters obtained in later studies employing more refined measurement techniques88,89 may allow the model to be improved, particularly in its estimates of spherical aberration.
In conclusion, our basic model can predict the changes in refraction, accommodative response with age and accommodation, and the results largely match clinical data. In the case of changes in spherical aberration with age and accommodation, predictions match the general trends observed in other studies, but absolute values are systematically more negative than experimental data. This model therefore has the potential to be a useful design tool in new approaches to correct the eye's optical errors, e.g. by using aspheric lenses or refractive surgery, and should also be of value in the analysis of the impact of changes in wavefront aberrations with accommodation and age on ocular depth-of-focus.
Conflicts of interestThe authors declare that there is no conflict of interest regarding the publication of this paper.
This work has been funded by the European Marie Sklodowska-Curie Grant AGEYE 608049-FP7-People to JZD, HR and NLG; and by the Fundación Séneca Grant, Región de Murcia 15312/PI/10 to NLG.