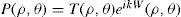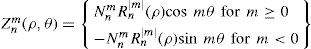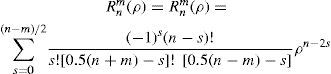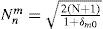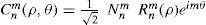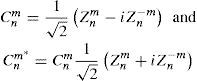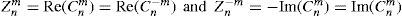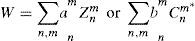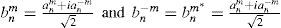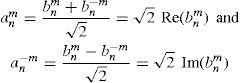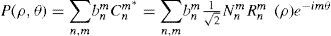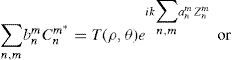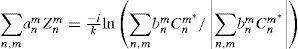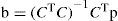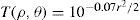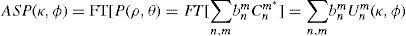To propose and evaluate Complex Zernike polynomials (CZPs) to represent general wavefronts with non uniform intensity (amplitude) in free-from transmission pupils.
MethodsThey consist of three stages: (1) theoretical formulation; (2) numerical implementation; and (3) two studies of the fidelity of the reconstruction obtained as a function of the number of Zernike modes used (36 or 91). In the first study, we generated complex wavefronts merging wave aberration data from a group of 11 eyes, with a generic Gaussian model of the Stiles-Crawford effective pupil transmission. In the second study we simulated the wavefront passing through different pupil stop shapes (annular, semicircular, elliptical and triangular).
ResultsThe reconstructions of the wave aberration (phase of the generalized pupil function) were always good, the reconstruction RMS error was of the order of 10−4 wave lengths, no matter the number of modes used. However, the reconstruction of the amplitude (effective transmission) was highly dependent of the number of modes used. In particular, a high number of modes is necessary to reconstruct sharp edges, due to their high frequency content.
ConclusionsCZPs provide a complete orthogonal basis able to represent generalized pupil functions (or complex wavefronts). This provides a unified general framework in contrast to the previous variety of ad oc solutions. Our results suggest that complex wavefronts require a higher number of CZP, but they seem especially well-suited for inhomogeneous beams, pupil apodization, etc.
Proponer y evaluar los polinomios de Zernike complejos (CZP) para representar frentes de onda de intensidad (amplitud) no uniforme a través de pupilas con cualquier tipo de transmisión.
MétodosConsisten en tres etapas: a) formulación teórica; b) implementación numérica, y c) realización de dos estudios evaluando la fidelidad de las reconstrucciones obtenidas en función del número de modos de Zernike usados (36 o 91). En el primer estudio generamos frentes de onda complejos usando aberraciones de onda reales de un grupo de 11 ojos, e incorporando (en todos los casos) un modelo genérico gaussiano de la transmisión efectiva a través de la pupila debida al efecto Stiles-Crawford. El segundo estudio consistió en simular el frente de onda a través de aperturas de diferentes formas (anular, semicircular, elíptica y triangular).
ResultadosLa reconstrucción de la aberración de onda (fase de la función pupila generalizada) fue satisfactoria en todos los casos; el error RMS fue siempre del orden de 10−4 longitudes de onda, independientemente del número de modos usados. La reconstrucción de la amplitud (transmisión), sin embargo, es muy dependiente de la complejidad del frente de ondas y del número de modos usados. En particular, se necesitan muchos modos de Zernike para reconstruir los bordes abruptos de las aperturas, debido a su elevado contenido en altas frecuencias espaciales.
ConclusionesLos CZP constituyen una base completa ortogonal capaz de representar funciones pupila generalizadas (o frentes de onda complejos). Esto proporciona un marco general, en contra de la variedad de soluciones ad oc propuestas previamente. Los resultados muestran que si aumenta la complejidad del frente de onda es también necesario incrementar el número de modos. En este sentido, los CZP parecen especialmente interesantes para frentes de onda inhomogéneos, pupilas apodizadas, etc.
The Zernike polynomial (ZP) expansion is widely used in optics because ZPs form a complete orthogonal basis on a circle of unit radius. Since many optical systems have a circular pupil, ZP expansion can be used to describe any real function at the pupil plane, such as the phase of a wavefront or the wave aberration. They are on the basis of many applications from optical design and testing,1,2 wavefront sensing,3 adaptive optics,4 wavefront shaping,5 corneal topography,6 etc.
In all these applications the main assumption is that the pupil (wavefront) or surface (topography) has a circular shape. However, in the human eye, the pupil may not be exactly circular, for example for peripheral visual angles, and its effective transmission is not constant but approximately Gaussian due to the wave guiding optical properties of the photoreceptors (Stiles-Crawford effect, SCE).7 In other words, the array of retinal photoreceptors is the last component of the optical system of the eye with a relevant impact on image and visual quality. In addition, there are many situations (visual testing, training, laser treatments, etc.) in which artificial pupil stops or special illumination, or simple vignetting modify the shape of the natural pupil. Most common artificial stops are circular, annular or semicircular, but one can find cases where the effective pupil can have almost any possible form. Many eyes display irregular pupil shapes or may present internal occlusions. Furthermore, the problem of representing free-form transmission pupils appears in any lens or optical system when working off-axis, especially for wide angle optics such as that of the eye. Not only the pupil is not circular, but its shape (eccentricity) changes with visual field and its orientation changes with meridian. The problem or representing the change of low and high order aberrations across the 2-dimensional visual field in a compact and homogeneous way still lacks a proper solution. Several solutions were proposed in literature for particular cases. For instance, Zernike annular polynomials were introduced to deal with annular stops.8,9 Affine (linear) transformations applied to circular pupils (and Zernike polynomials) permit to compute the effects of rotations, translations or two-dimensional scaling10 to pass from circular to elliptical geometries11 and vice versa. It is also possible to orthogonalize Zernike polynomials for general aperture shapes.12
A different but related issue is the case of inhomogeneous transmission pupils, or inhomogeneous illumination beams, or a combination of both. In the human eye, the SCE means that the effective pupil transmission of the eye is approximately Gaussian.7 Modern light sources such as lasers, LEDs, or new optical elements such as axicons proposed to compensate prebyopia13 produce with inhomogeneous amplitude wavefronts: Gaussian, Bessel or associated beams.14,15 Nowadays apodized multifocal intraocular lenses (with inhomogeneous pupil transmission16) may offer improved performance over standard IOLs after cataract surgery.17
This brief overview suggests a wide potential field of application of a proper description of general complex wavefronts, with free-amplitude and free-phase distributions. The purpose of this work is to study the ability of CZPs to represent these general complex wavefronts in human eyes. To this aim we study two different cases: First the Stiles-Crawford apodization as an example of inhomogeneous pupil transmission (or inhomogeneous amplitude). This is especially relevant as this is an intrinsic property of the optical system of the eye, and also because methods such as laser ray tracing can measure both the amplitude (from the relative intensity of spots) and phase (from the centroid of spots) of the wavefront.18 Second we study different types of pupil apertures. As we said above, there exist effective ad hoc solutions even for general pupil shapes.12 Also for inhomogeneous transmission the standard approach is to use two separate real functions for T and W. In this context, there are two main potential benefits of using CZPs. On the one hand, they provide a unified and generalized solution for a wide variety of pupil shapes and transmissions, since the CZPs form a complete orthogonal basis able to represent any complex wavefront in monochromatic light. The only constraint imposed to the wavefront is that it has to be fully contained within a “reference” circle. On the other hand, as we discuss in Section 4, the generalized Nijboer-Zernike (N-Z) approach permits one to use the same set of coefficients to describe both the wavefront and the amplitude spread function (image quality), by simply changing the basis functions.19,20 This may be especially relevant in visual optics applications. In fact, Braat and co-workers21 introduced CZPs to compute PSFs using the generalized N-Z theory.
Complex zernike polynomialsFrom now on we will consider a monochromatic wavefront at the pupil plane described as a generalized pupil function (amplitude and phase) of spatial polar coordinates:
This complex function is defined within a circle of unit radius, which means that the radial coordinate ρ=r/R is normalized by the pupil radius R of a reference circle which contains the wavefront. T represents the wavefront amplitude, or effective pupil transmission and kW is the phase, where W(ρ,θ) is the wave aberration and k is the wave number.
Basic formulationLet us start with a brief review of the formulation of Zernike polynomials. The expression for the real polynomials is (ANSI Z80.28 standard) within the circle of unit radius is:
where ρ,θ are polar coordinates, and the radial part is given by:A normalization factor is included to guarantee orthonormality:
The complex version can be obtained by considering couples of polynomials with angular frequencies +m and −m, corresponding to the real and imaginary parts respectively. After the required normalization by a factor 2 it is straightforward to arrive to the expression for the complex ZPs.
This means that we construct a couple of a complex C and its conjugated C* (or couple of +m, −m) from its respective couple of +m, −m real Z polynomials:
To recover the real polynomials we only need to take the real and imaginary parts:
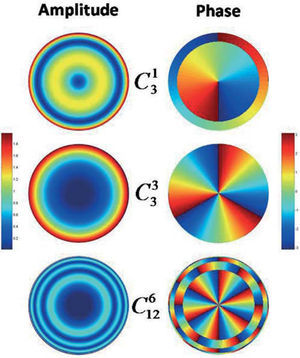
Figure 1 shows some examples of the amplitude and phase of the CZPs. Note that the amplitude 12Nnm abs (Rnm(ρ)) only depends on radius, whereas the phase term sign Rnm(ρ) eimθ is a function of both coordinates (ρ,θ) (the phase is a pure angular frequency only for m=n that is when R is always positive, such as for C33).
Representation of real and complex functionsThe classical expansion of a real function, such as the wave aberration W in terms of ZPs is
where anm are real and bnm are complex coefficients respectively. Note that in the complex expansion the polynomials are conjugated. It is immediate to show that for real functions, the complex coefficients can be computed from the real ones:And conversely,As a consequence of these expressions, for real functions bnm=bnm* the coefficients with −m and +m are conjugated, which means that they are not independent (but redundant). This is a general property of this type of expansions, such as complex Fourier series, etc. Therefore, it is totally equivalent to use real or complex versions of ZPs to represent wave aberrations (or real functions in general), and Eqs. 9 and 10 permit to pass from the real to the complex basis and conversely. However, these relations do not hold for complex functions in general.
For complex wavefronts, we simply combine Eqs. 1, 5 and 8 to obtain:
where bnm are the complex coefficients of the expansion. Note the negative sign in e−imθ to take into account the complex conjugation Cnm*. The real coefficients a are not defined in this case. Nevertheless, when W is given as an expansion of real ZPs it is straightforward to express the relationship between the real and complex coefficients:For practical implementation we will assume a limited number of coefficients and sampling points in the wavefront, so that these equations can be expressed in vector-matrix notation (see next Section).
Implementation and resultsNumerical methodsIn the numerical implementation, we work with discrete (sampled) wavefronts so that the continuous expressions translate into a matrix-vector formulation. We applied a square sampling grid, and took 3720 points within a circle (34 samples along its radius.) The samples of the complex wavefront were arranged as the 3720 components of a column vector p. In the series expansion of Eq. 11, we considered two cases with maximum order n=7, that is 36 polynomials or modes, and n=12, which means 91 modes. In each case we constructed a complex matrix C, of 3720×36 and 3720×91 respectively. Then, Eq. 11 becomes p=Cb where b is another column vector formed by either 36 or 91 complex coefficients. To compute the coefficients b of the expansion we applied a standard least squares fit to this strongly oversampled set. This is equivalent to apply the pseudoinverse of C to the data:
Note that Eq. 12a means that vector p=t.eikZa, where the dot product means element by element. Conversely a=−ik(ZTZ)−1ZT(lnCb=ln|Cb|).Stiles-Crawford apodizationThe first numerical study consisted of representing the generalized pupil function (Eq. 1) of a group of 11 human eyes with CZPs with a variety of pupil sizes and RMS wavefront errors. The experimental wave aberration data (W) were taken from a previous study,22 whereas a generic Gaussian model7 was used to describe the amplitude for all eyes:
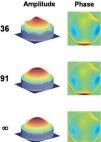
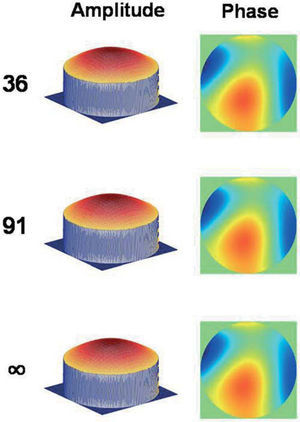
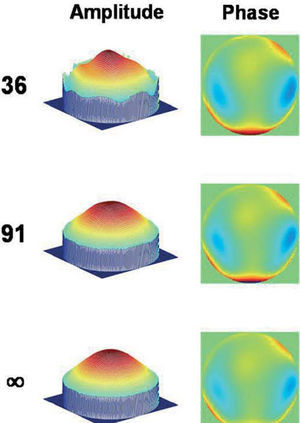
where the argument is divided by 2 to pass from intensity to amplitude. (Note r is the physical radial coordinate is r=ρR in mm.) The quality of reconstructions with CZPs is high for most eyes. The RMS error for the wave aberration (phase) is of the order of 10−4 wavelengths in all cases. The average is 5×10−4±2×10−4 λ both for 36 and 91 modes reconstructions, which is well below the sensitivity of experimental aberrometers. For the amplitude the RMS error improves with the number of complex Zernike modes used. For reconstructions with 36 complex modes (up to 7th order), the average RMS error (11 eyes) was 1.6×10−2±1.8×10−2 pupil transmittance. The maximum reconstruction error (worst case) was 4.7×10−2 for subject RN (OD) who also had the largest pupil diameter 6.5 mm and the largest wave aberration 0.5 mm RMS. The minimum error (best case) was 2.8×10−3 for subject JA (OD) who had the smaller pupil, 4.5 mm, and only 0.1 mm RMS wave aberration. When we increase the number of modes to 91 (up to 12th order), the phase reconstruction does not improve significantly (as it was already good for 36 modes), but the amplitude improves so that the average RMS reconstruction error is one order of magnitude lower 1.6×10−3±2.6×10−3 now. The values for the same worst and best cases also improves, being 7.1×10−3 for RN (OD) and 3.7×10−5 for JA (OD). Figs. 2 and 3 show the original and reconstructed amplitude (left panels) and phase (right panels) corresponding to these two best (JA) and worst (RN) cases, respectively. In these and following figures, the upper row corresponds to the reconstruction with 36 modes; the central row to that obtained with 91 modes; whereas the bottom row shows to the ideal case, labeled with ∞ to mean the exact result expected when the series are not truncated (in fact label ∞ correspond to the initial data, T and W respectively). The reconstructions look visually indistinguishable from the original when the error is clearly below 10−2, which is always the case for phase. On the contrary, the amplitude display clearly visible differences with the original in several 36 modes reconstructions (see Fig. 3 upper row). These eyes (3 out of 11) have larger pupils and larger higher order aberrations than the mean.Reconstructions of the amplitude (left) and phase (right) of the wavefront for subject RN OD. Original and reconstructions as in Fig. 2.
In summary, CZPs seem able to represent the generalized pupil function (amplitude and phase simultaneously) of human eyes. Nevertheless, for large pupils, since the amount of higher order aberrations is usually large too, it is necessary to use more complex modes (higher orders) to obtain an accurate representation.
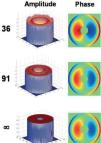
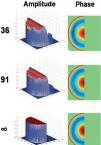
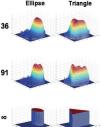
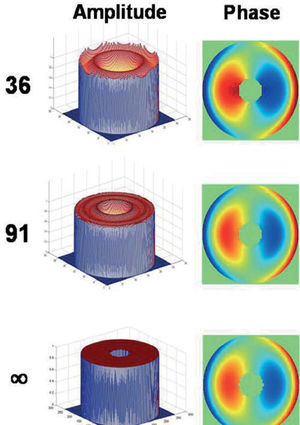
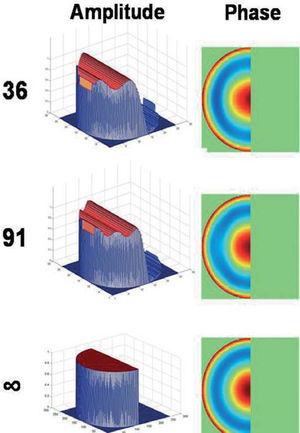
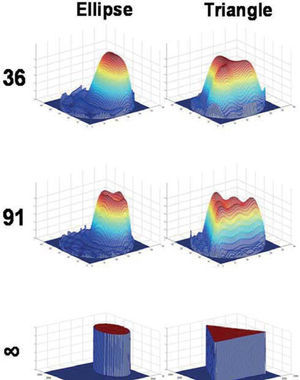
Free-form pupil stopsThe next study consisted in numerical simulations. Here we considered three different wavefront aberrations: (1) one wavelength (λ) of pure spherical aberration W=Z40; (2) λl of pure coma W=Z31 and (3) one example of ocular wave aberration taken from the above study. In this case the pupil transmission is binary. This means that we consider different pupil stop shapes within the reference circle, and the transmission is assumed to be one (maximum) within the aperture and zero outside. In particular we simulated annular (Fig. 4), semicircular (Fig. 5), elliptical or triangular (Fig. 6) pupil stops. The phase is pure coma in Figure 4 and pure spherical aberration in Figure 5. In Figure 6 only the amplitude is displayed as the phase reconstruction was similar to that of previous figures. We also simulated the case of Gaussian apodization (as in Section 3.2) for pure coma and pure spherical aberration.
Reconstruction of a wavefront with one lambda of pure coma Z13 through an annular aperture. Original and reconstructions as in Fig. 2.
Reconstruction of a wavefront with one lambda of pure spherical aberration Z04 through a semicircular aperture. Original and reconstructions as in Fig. 2.
The accuracy obtained for the reconstructions, in terms of the RMS difference between reconstructed and original data (amplitude and phase respectively) are listed in Table 1 for case (2), coma. The results for the other two cases (spherical aberration and real ocular wave aberration) are not included since they are totally equivalent (close RMS values). The phase reconstruction was good in all cases, no matter the type of amplitude function or pupil shape. The RMS phase error is of the order of 6×10−4 (λ units) independently from the number of modes considered, as in the former study. On the contrary, the reconstruction of the amplitude is strongly dependent on the initial transmittance function T. For the circle (trivial case, first column in Table 1) the reconstruction is basically perfect, since the circle is fully represented by the piston term C00 = 1. When T is Gaussian, the reconstruction is good, but improves further by increasing the number of modes (about three orders of magnitude when passing from 36 to 91 modes). This result is also consistent with that obtained with real eyes. In the other cases (annular, semicircle, ellipse, triangle) the number of modes used here seems insufficient to accurately represent the sharp edges of the stop. In fact, we can observe ringing or wavy-like artifacts in the reconstructions, which tend to improve by increasing the number of modes. The amplitude RMS errors are now of the order of 10−1 even for 91 modes. This seems the main limitation of this method: the reconstruction of sharp edges in the amplitude function requires higher order modes (frequencies), whereas the method seems to work well when both modulus and phase are smooth functions.
RMS reconstruction errors for the different pupil transmissions and for 1 λ of pure coma. The errors for other aberrations are totally equivalent
| Circle | Gaussian | Annular | Semicircle | Ellipse | Triangle | |
| Amplitude | ||||||
| 36 modes | 1.9×10−14 | 2.6×10−3 | 1.5×10−1 | 1.5×10−1 | 1.7×10−1 | 2.4×10−1 |
| 91 modes | 2.5×10−15 | 3.1×10−6 | 1.0×10−1 | 1.2×10−1 | 1.3×10−1 | 1.8×10−1 |
| Phase | ||||||
| 36 modes | 5.7×10−4 | 5.7×10−4 | 5.8×10−4 | 5.7×10−4 | 6.2×10−4 | 5.8×10−4 |
| 91 modes | 5.7×10−4 | 5.7×10−4 | 5.7×10−4 | 5.7×10−4 | 6.3×10−4 | 5.8×10−4 |
In this article we propose the use of complex Zernike polynomials to represent complex wavefronts, or generalized pupil functions, with free-from amplitude and phase. The main advantage is that the CZPs basis provides a unified framework as opposed to a series of ad hoc solutions published in the literature for each type of aperture. Our numerical results are highly satisfactory whenever both amplitude and phase are smooth functions within the reference circle. This could be especially useful to represent pupil apodization, complex filters, or inhomogeneous beams (Gaussian, Bessel, etc.) Nevertheless, our results suggest that the number of modes (or order of polynomials) needed to obtain a high fidelity representation increases with the degree of complexity. A totally different behavior was found for amplitude and phase. The reconstruction of phase was always good (regardless of the number of modes), whereas the amplitude showed a strong dependency on both the number of modes and the amount of high order aberrations. A plausible explanation for the good phase reconstructions could be that the initial values of phase were also given in terms of real ZP expansions, and real and complex ZPs are closely related. On the contrary, the amplitude was either a Gaussian or binary geometric masks. In fact, the main limitation appears when attempting to represent discontinuities, such as sharp edges, or very high frequency features with a low number of modes. When one tries that, then the reconstruction shows smoothed versions of edges with ringing or wavy artifacts around. These effects are analogous to the aliasing artifacts that one finds in Fourier analysis due to spectral overlapping.23 To avoid this type of artifacts, when computing the Fourier transform, the signal must be band-limited and the minimum sampling (Nyquist) frequency has to be double that the maximum frequency present in the signal. In Fig. 1 we can appreciate that the CZPs show a sort of radial and angular frequencies associated to n and m. Roughly speaking, in order to represent a small (high frequency) feature in the wavefront, we need to include higher order modes which may display features of the same size.
In the examples studied so far, the phase was a smooth function (ZP expansion), what is a common situation in optics. In these cases, and when the accuracy demand is important mainly for the phase of the wavefront (what is also usual), then one can get reasonable results with a limited number of modes such as in the present implementation (36 or 91 modes). When very high frequencies are present and accuracy requirements are high too, then ad hoc solutions or Fourier series may be more efficient computationally. This is mainly because the evaluation of long polynomial strings is time consuming. However, CZPs present important advantages. As we said in the introduction, the N-Z theory19 of image formation shows that it is possible to establish a linear relationship between the modal expansion of the image of a point source, the amplitude spread function (ASF), and a modal expansion of the complex wavefront.20 If we neglect constants:
where functions Unm(κ,ϕ)=FT[Cnm*(ρ,θ) are the Fourier transforms of CZPs. They have an analytical expression similar to that of ZPs, but in terms of Bessel functions,21 instead of radial polynomials Rmn In other words, the same coefficients describe the generalized pupil function and the image of a pint source. For incoherent illumination, the point-spread function, PSF, is the squared modulus of the ASF:PSF(κ, ϕ)=ASF(κ, ϕ)2. In addition to saving computing time, this theory permits a direct, simple connection between wavefront and image quality metrics could have a high potential in applications in visual optics, including the optical design of advanced optical elements. The implementation and practical applications of Eq. 15 will be the subject of future work.Conflict of interestsAuthors declare that they don’t have any conflict of interests.
This work was supported by the Comisión Interministerial de Ciencia y Tecnología, Spain, under Grant FIS2008-00697.