In children under 20 years, refractive development targets a cycloplegic refractive error of +0.5 to +1.5D, while presbyopes over 40 years generally have non-cycloplegic errors of ≥ +1D. Some papers suggest these periods are separated by a period of myopic refractive error (i.e., ≤ –0.50D), but this remains unclear. Hence, this work investigates the mean cycloplegic refractive error in adults aged between 20 – 40 years.
MethodsIn 2002 a cross-sectional study with stratified cluster sampling was performed on the population of Tehran, providing cycloplegic and non-cycloplegic refractive error data for the right eyes of 3,576 participants, aged 30.6±18.6 years (range: 1–86 years). After grouping these data into age groups of 5 years, the refractive error histogram of each group was fitted to a Bigaussian function. The mean of the central, emmetropized peak was used to estimate the mean refractive error without the influence of myopia.
ResultsThe mean cycloplegic refractive error at the emmetropized peak decreased from +1.10±0.11D (95 % confidence interval) to +0.50±0.04D before 20 years and remains stable at that value until the age of 50 years. The non-cycloplegic refractive error also sees a stable phase at 0.00±0.04D between 15 – 45 years. After 45 – 50 years both cycloplegic and non-cycloplegic refractive error become more hypermetropic over time, +1.14±0.12D at 75 years.
ConclusionsThe cycloplegic refractive error in adults is about +0.50D between 20 – 50 years, disproving the existence of the myopic period at those ages.
It was recently suggested that emmetropization targets a cycloplegic refractive error of +1D by the age of 2 years,1–3 which is theorized to protect against myopization. After 2 years the eye is in homeostasis, a period during which the axial growth and lens power loss are matched to keep the refractive error near +1D.1,2 Emmetropization does not occur at the same rate in all eyes, however, causing the distribution of the refractive error to gradually become narrower by the age of 6 years.1,4,5 Especially in populations growing up with a high exposure to outdoors light, this process can even continue until as late as 12 years,6 with a clustering of the refractive error around moderate hyperopia without increases in myopia, showing a late emmetropization.
Without cycloplegia, the refractive target of emmetropization is much closer to 0D,7 suggesting that, under physiological conditions, the low hypermetropic refraction is neutralized by the accommodative tonus. This tonus of about +0.75D may be linked to night myopia,8,9 the phenomenon causing someone who is emmetropic in photopic circumstances to experience blurred distance vision in the dark due to a lack of visual stimuli. Hence, emmetropes may experience a night myopia of–0.75D, corresponding with the change from the cycloplegic baseline refractive error as confirmed consistently in young participants.
Although the course of refractive development is quite well known in children, it remains unclear what the normal refractive target is in young adults (aged 20 – 40 years) due to an overall lack of studies in this age group. Moreover, existing studies are non-cycloplegic and often focused on subgroups prone to myopia that are not representative for the general population (e.g., people in a clinic or university students). This has led to the idea10–12 that there may be a myopic phase in healthy young adults, but as myopia generally does not reverse, a slight myopic shift seen in young adults in cross-sectional samples seems unrealistic on a prospective basis. Finally, many clinicians seem to be under the impression that eyes of this age do not undergo any active development, even though myopia can still emerge or progress further in this group showing that the mechanism governing eye growth is still active.13 The high prevalence of myopia in young adults causes the refractive distribution to skew, so that neither the average nor the median of the refractive error can provide an accurate estimate of the target refractive error unbiased by myopia. Consequently, such estimates in young adults show a wide range between low hypermetropia14,15 and low myopia.10–12 After the age of 40 years the refractive error shows a gradual return towards low hypermetropia until 70 years,10–12,15 followed by a final shift back towards emmetropia that is induced by cataract.11,12,15,16
The uncertainty about the average refractive error in young adults leaves an important question about the long-term target of normal refractive development. To address this issue, the cycloplegic and non-cycloplegic refractive errors of the Tehran Eye Study (TES) are reanalyzed using Bigaussian analysis, which is able to negate the influence of myopia that affected an earlier analysis.17 The TES data are ideal for this purpose as they represent the only large population study in the literature with cycloplegic data for young adults.
Material and methodsParticipantsThe Tehran Eye Study was conducted over a period of 4 months in 2002 at the Noor Vision Correction Centre. Details of the sampling strategy and methodology have been published elsewhere.18 In brief, participants were selected from the population of Tehran through stratified cluster sampling. In total there were of 3576 participants with a complete examination. These were divided into subgroups according to age in blocks of 5 years. Each category contained at least 100 people, which was deemed sufficient to characterize the refractive distribution. Only data of the right eyes were used to avoid the influence of the strong correlation between the eyes of the same individual. The examination consisted of an automated autorefractometry measurement (Topcon KR 8000; Topcon Corporation), both before and 30 min after 2 drops of 1 % cyclopentolate were instilled in both eyes.
TES was conducted in accordance with the tenets of the Helsinki Declaration and received approval from the Ethics Committees of the Noor Ophthalmology Research Centre, and the National Research Centre for Medical Sciences (Ref. MM/T/1633). All participants gave informed consent prior to examination, which did not include any intervention or unusual procedures in clinical practice.
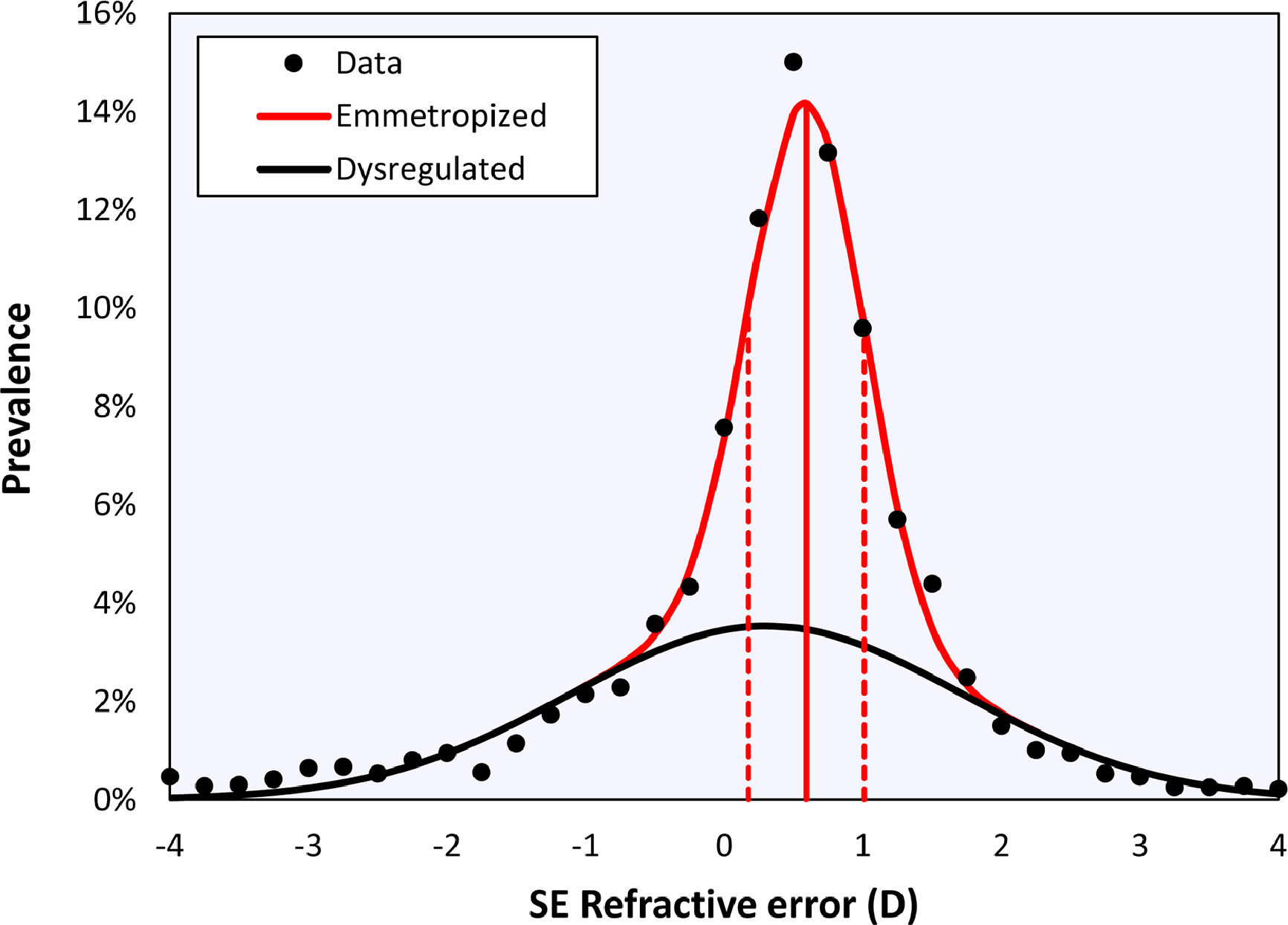
Bigaussian fitRefractive distributions are generally leptokurtic and skewed due to the presence of myopia. Although they may be characterized using a mean with confidence intervals or a median with an interquartile range, the most accurate representation is a sum of two Gaussian functions (Figu. 1).19,20 These two Gaussians represent a sharp peak centered at emmetropia or low hypermetropia, corresponding with eyes that emmetropized well (‘emmetropized’), and a broad peak centred at low myopia, corresponding with eyes in which the emmetropization did not occur optimally (‘dysregulated’).20
Bigaussian fit applied to the cycloplegic spherical equivalent refractive error data of right eyes over the entire age range, including the emmetropized (red) and dysregulated (black) modes. Solid vertical red line represents the mean of the emmetropic peak, dotted lines represent the standard deviations.
In the context of this work, the use of Bigaussian fits has a marked advantage over mean or median values of the refractive error, which are likely skewed towards more negative values due to myopia. The mean value of the emmetropized peak, on the other hand, is not affected by the myopes in the population and will therefore provide a more accurate estimate of the normal refractive error in young adults.
All calculations are performed in Excel (v365, Microsoft) and Matlab (v2021a, The Mathworks). In all analyses a significance level of p < 0.05 was deemed significant.
ResultsThe histogram in Fig. 1 shows the distribution of the cycloplegic spherical equivalent refractive in bins 0.25D wide. Fitting a Gaussian function and the sum of two Gaussian functions gave coefficients of determination of r2= 0.962 and r2= 0.994, respectively. The F-test suggests that the Bigaussian representation is better able to capture the specific shape of the distribution (F=72.21, p < 0.001). The Bigaussian function is therefore used in the following.
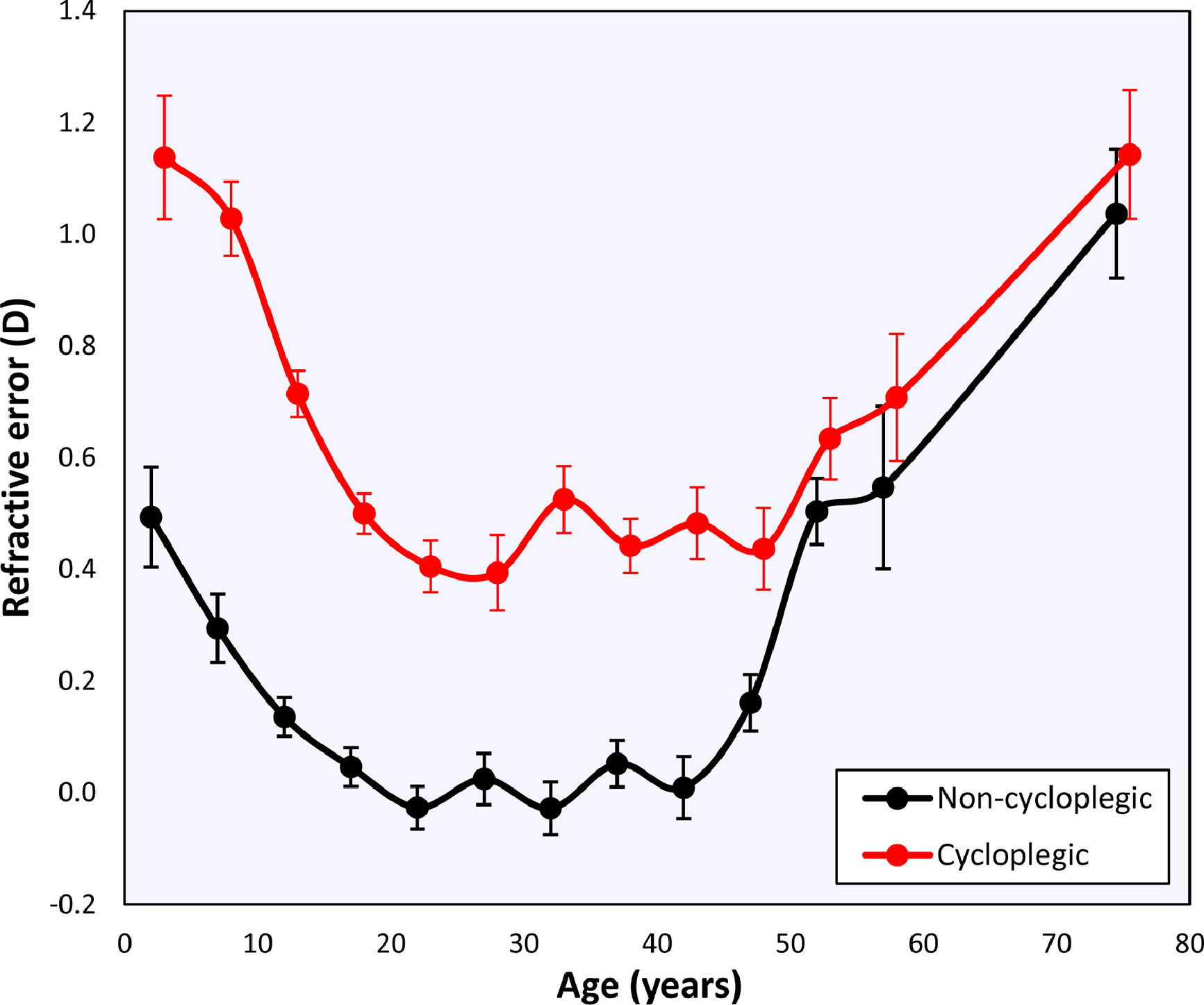
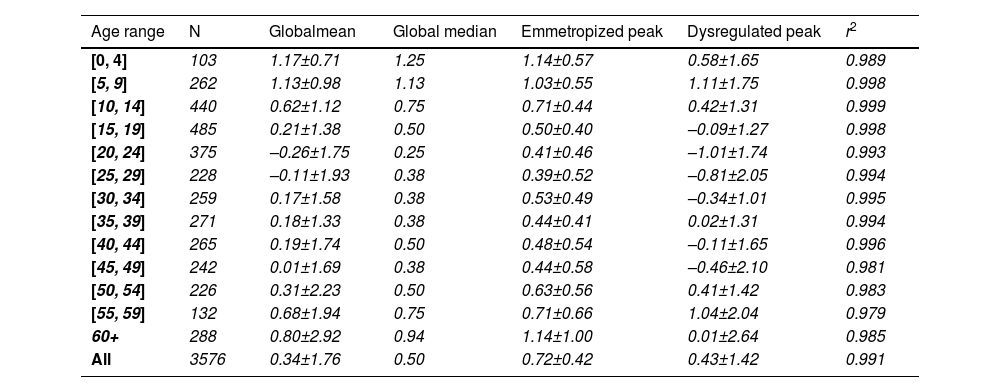
Changes with ageThe global mean refractive error under cycloplegia decreases with age during childhood until it reaches a mildly myopic minimum (–0.26±1.75 D) at 20 – 24 years, after which it increases again (Table 1). This agrees with the previous literature and reflects the influence of myopia incidence in adolescents and the known hypermetropization in older eyes due to changes in the gradient index of the lens.21,22 Applying Bigaussian fits to histograms with bins 1D wide for each age group, the emmetropized peak remains inside a range of [+0.39D, +0.50D] for 15 – 49-year-olds and later increases towards hypermetropia (Table 1, Fig. 2). The global median seems to follow a similar course as the position of the emmetropized peak.
Mean cycloplegic refractive errors (mean ± StDev) of the emmetropized and dysregulated peaks determined for each age group using Bigaussian fits.
| Age range | N | Globalmean | Global median | Emmetropized peak | Dysregulated peak | r2 |
|---|---|---|---|---|---|---|
| [0, 4] | 103 | 1.17±0.71 | 1.25 | 1.14±0.57 | 0.58±1.65 | 0.989 |
| [5, 9] | 262 | 1.13±0.98 | 1.13 | 1.03±0.55 | 1.11±1.75 | 0.998 |
| [10, 14] | 440 | 0.62±1.12 | 0.75 | 0.71±0.44 | 0.42±1.31 | 0.999 |
| [15, 19] | 485 | 0.21±1.38 | 0.50 | 0.50±0.40 | –0.09±1.27 | 0.998 |
| [20, 24] | 375 | –0.26±1.75 | 0.25 | 0.41±0.46 | –1.01±1.74 | 0.993 |
| [25, 29] | 228 | –0.11±1.93 | 0.38 | 0.39±0.52 | –0.81±2.05 | 0.994 |
| [30, 34] | 259 | 0.17±1.58 | 0.38 | 0.53±0.49 | –0.34±1.01 | 0.995 |
| [35, 39] | 271 | 0.18±1.33 | 0.38 | 0.44±0.41 | 0.02±1.31 | 0.994 |
| [40, 44] | 265 | 0.19±1.74 | 0.50 | 0.48±0.54 | –0.11±1.65 | 0.996 |
| [45, 49] | 242 | 0.01±1.69 | 0.38 | 0.44±0.58 | –0.46±2.10 | 0.981 |
| [50, 54] | 226 | 0.31±2.23 | 0.50 | 0.63±0.56 | 0.41±1.42 | 0.983 |
| [55, 59] | 132 | 0.68±1.94 | 0.75 | 0.71±0.66 | 1.04±2.04 | 0.979 |
| 60+ | 288 | 0.80±2.92 | 0.94 | 1.14±1.00 | 0.01±2.64 | 0.985 |
| All | 3576 | 0.34±1.76 | 0.50 | 0.72±0.42 | 0.43±1.42 | 0.991 |
The non-cycloplegic refractive error shows a similar behavior, with an emmetropic period between 20 – 40 years and a hypermetropic increase at 45 – 49 years. The latter reflects the loss in accommodation and the internal changes in lens gradient index that produce a loss of intrinsic lens power with age21,22 (Fig. 2).
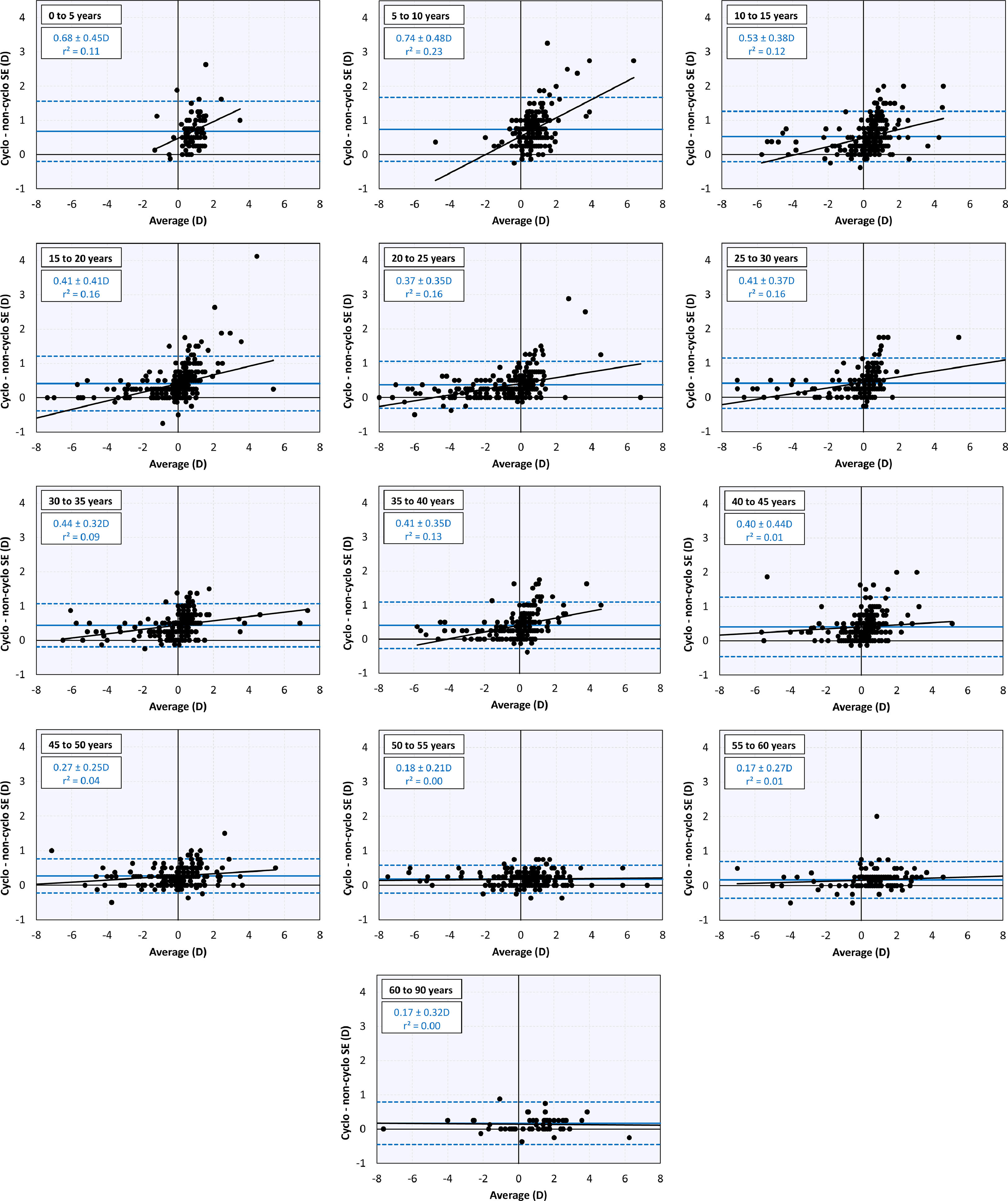
Comparison between cycloplegic and non-cycloplegic refractive errorAt younger ages there is a positive correlation between the difference between cycloplegic and non-cycloplegic refractive errors and the average of both (Fig. 3). This positive correlation is lost as the subjects become older and the difference between cycloplegic and non-cycloplegic refractive error decreases. There are, however, many subjects with big differences between both measurements.
DiscussionThis work used Bigaussian fits to improve the previous estimate17 of the changes in refractive errors in the Teheran Eye Study. The results clearly confirm that the cycloplegic refractive error in non-myopes between 20 – 50 years old is about +0.5D (Fig. 2), extending Morgan et al.’s3 report to this effect for children well into adulthood. Meanwhile, the non-cycloplegic refractive error remains at plano until 45 years due to latent accommodation.
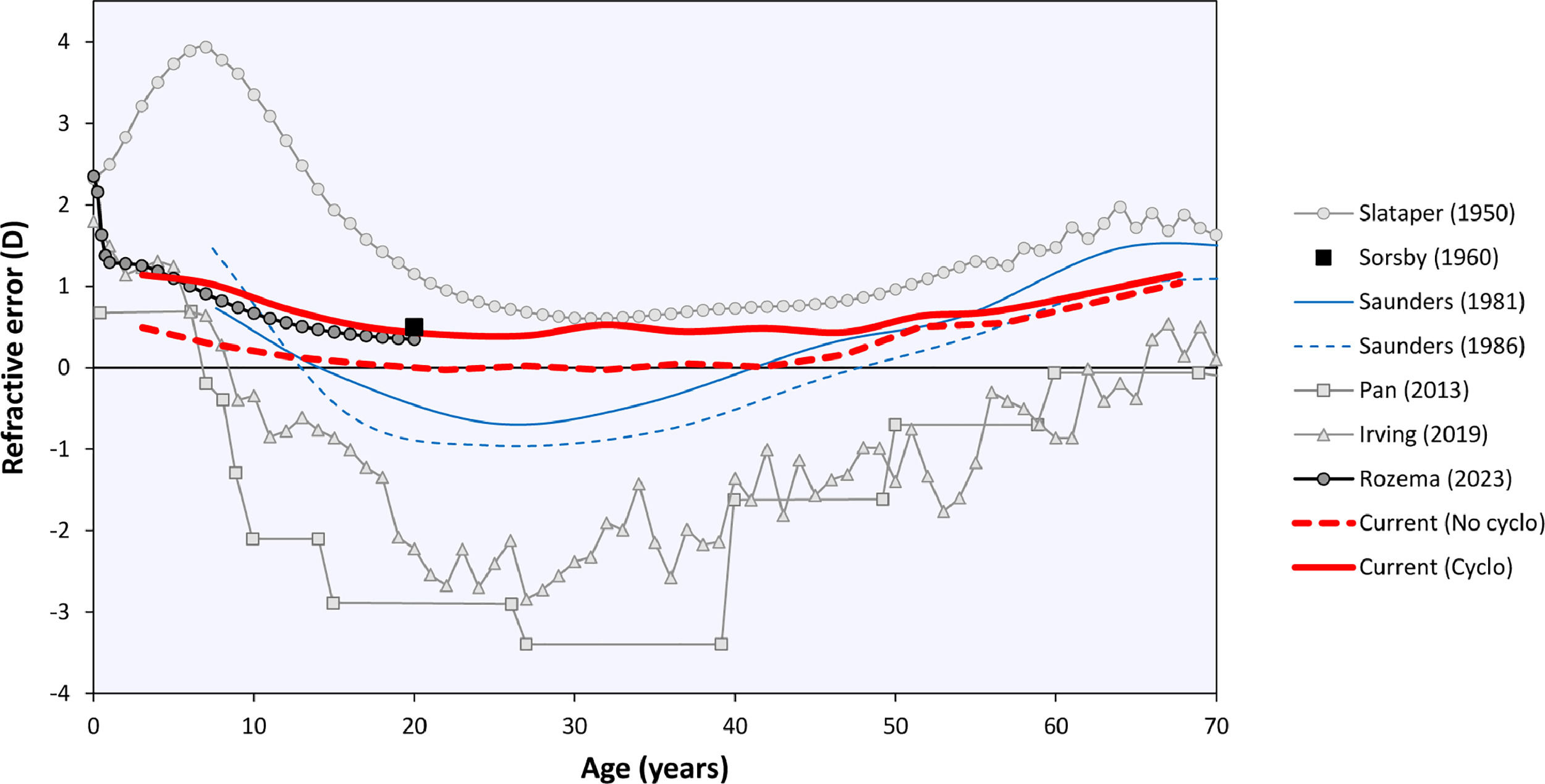
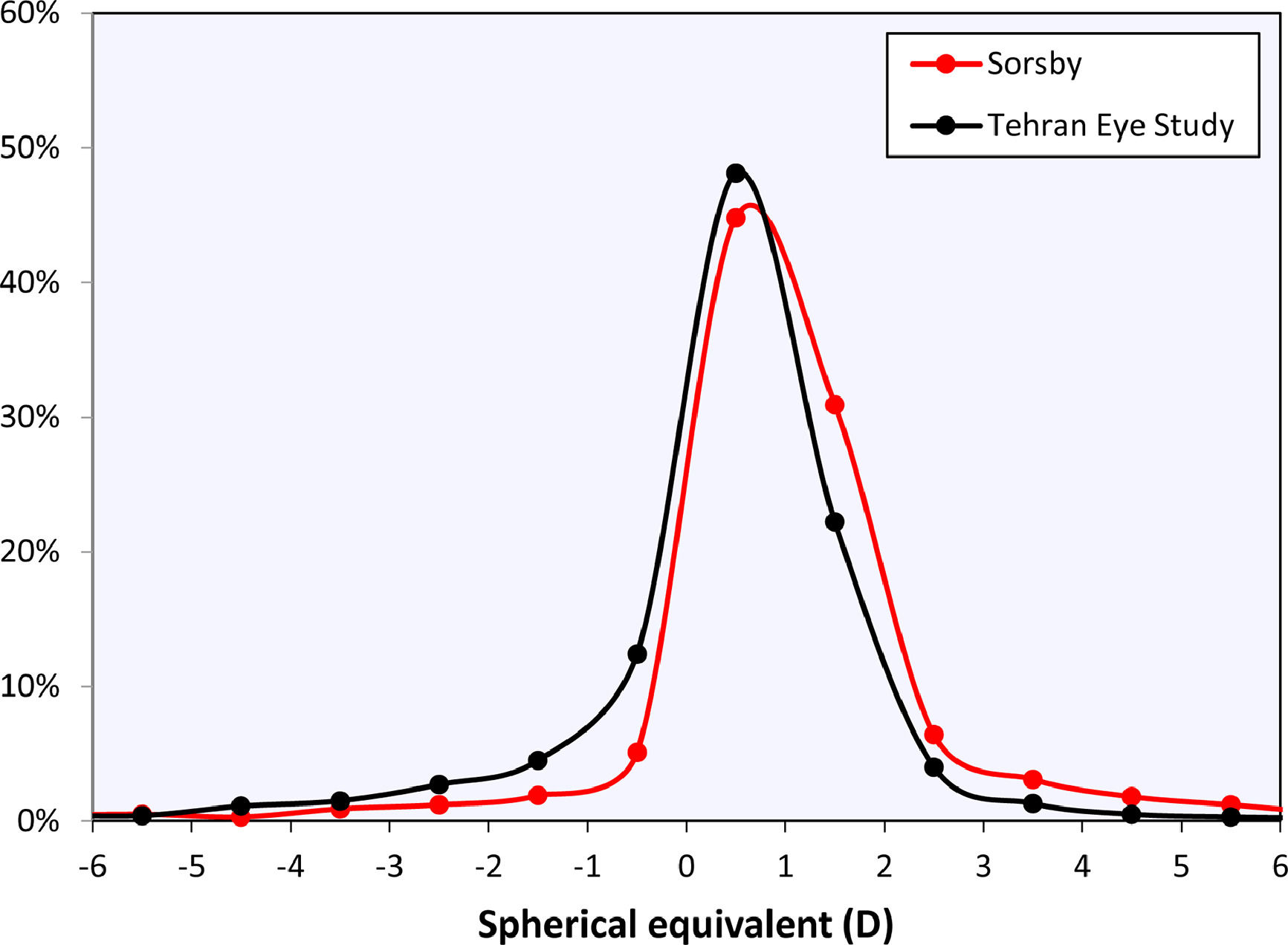
The curves in Fig. 2 may be compared to the refractive error changes in the literature (Fig. 4). Among those, Sorsby's 1960 paper14 with the cyclopleged data for 20-year-old army recruits is especially important, reporting a peak “between 0 and +1D”. Interpreting this as the mean of both values, +0.5D, this closely agrees with the current results. Furthermore, the distribution of Sorsby's population closely matches that of the current data (Fig. 5). The cycloplegic refractive errors reported by Slataper15 appear very high overall, especially before 20 years of age, but show a stable period between 25 – 45 years at about +0.6D. Finally, the meta-regression curve by Rozema,2 based solely on cyclopleged reports from the literature, gives a value of +0.35D at 20 years, again agreeing with the current result. Four other studies were considered unsuitable for comparison with the current analysis: one study23 with a large myopic influence, and three others10–12 presenting non-cycloplegic, clinical populations with a large myopic influence.
The current analysis was performed using the Teheran Eye Study data, which are especially suited for this analysis as they were the only large-scale cycloplegic data in the age range of interest. Moreover, the TES data were collected 22 years ago before the peak of the myopia epidemic in Asia, leading to a relatively high proportion of emmetropes (Fig. 1). Previously, these data helped demonstrate that non-cycloplegic refraction cannot be reliably used to determine myopic and hypermetropic refractive errors due to accommodation, making cycloplegic refraction the gold standard for epidemiological and clinical studies.24 Consequently, recent efforts in myopia prevention25 focus on detecting children who are plano under cycloplegia26 as they lack a physiological hypermetropic reserve that protects them from developing myopia.27 The current results suggest that during normal refractive development the eye tries to preserve this cycloplegic hypermetropic reserve at +0.5D, making this the target of emmetropization by early adulthood. Note that this is not the same as a hypermetropic reserve under normal accommodative tonus without cycloplegia, where the refraction is near plano for distance viewing and accommodation provides clear near vision. Furthermore, it important to distinguish the current results for objective refraction from cycloplegic and non-cycloplegic subjective refraction that, in the hands of experienced clinicians, could lead to somewhat different refractive values.
Finally, a Bigaussian fitting method was used in this work to distinguish between the emmetropized and dysregulated sections of the population.20 This method is easily implemented in Matlab or R and may be of use in future studies to disregard the influence of myopia seen in some earlier studies based on global mean or average values.28
This project was partly supported by a grant from the Iranian National Research Centre for Medical Sciences.