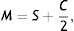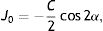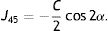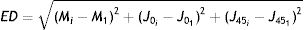To investigate a new algorithm to perform an automated non-cycloplegic refraction in adults.
MethodsFifty healthy subjects were measured twice (test–retest) with the new automated subjective refraction method and with the conventional clinician subjective refraction procedure. Objective refraction was also measured with the Grand Seiko WAM-5500 autorefractor. The new automated method was inspired on the root finding bisection algorithm and on the Euclidean distances in the power vector domain. The algorithm was implemented in a computer that was synchronized with a customized motorized phoropter. Repeatability was mainly assessed with the within-subject standard deviation (Sw) and accuracy was mainly assessed with the limits of agreement.
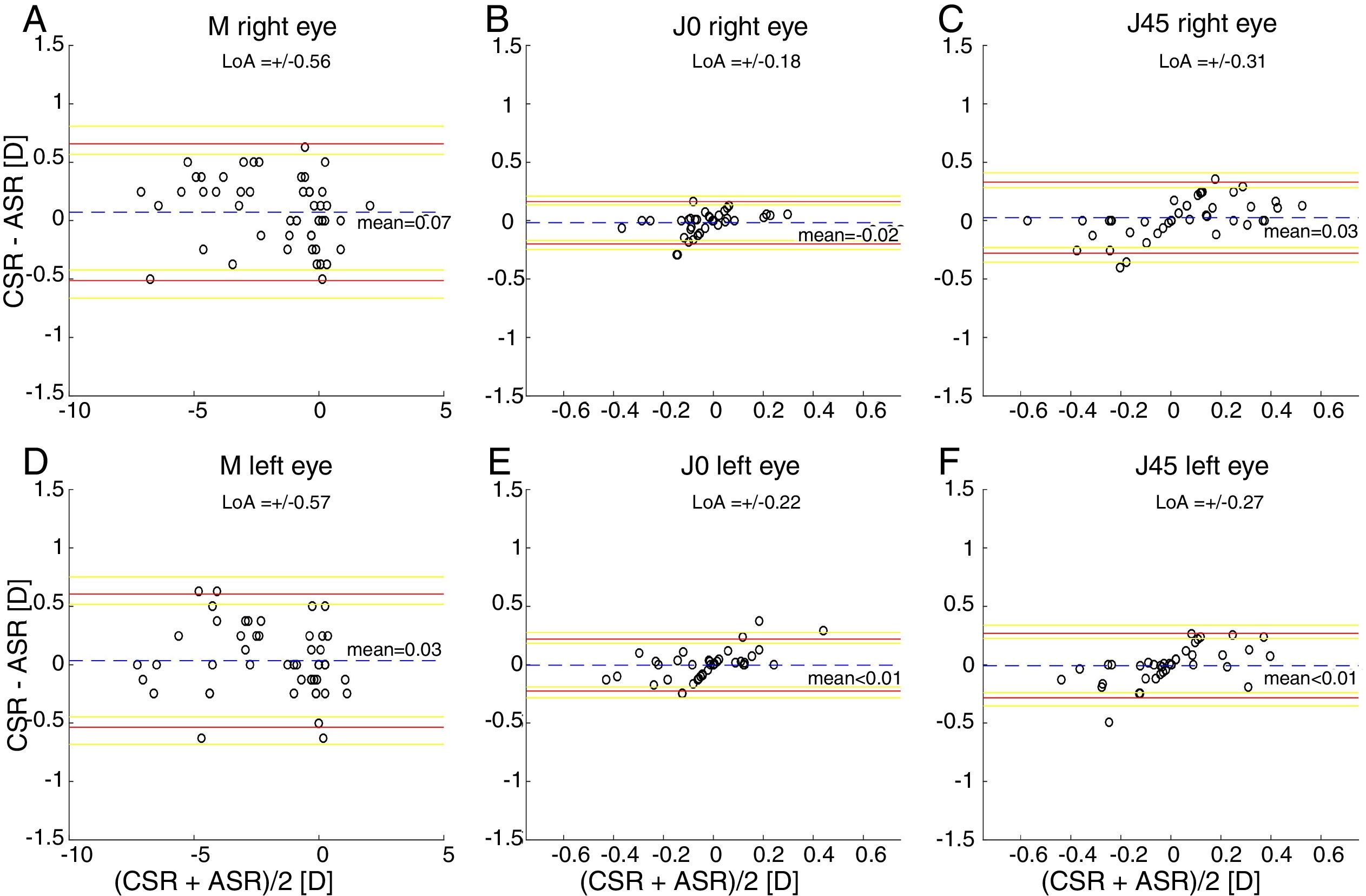
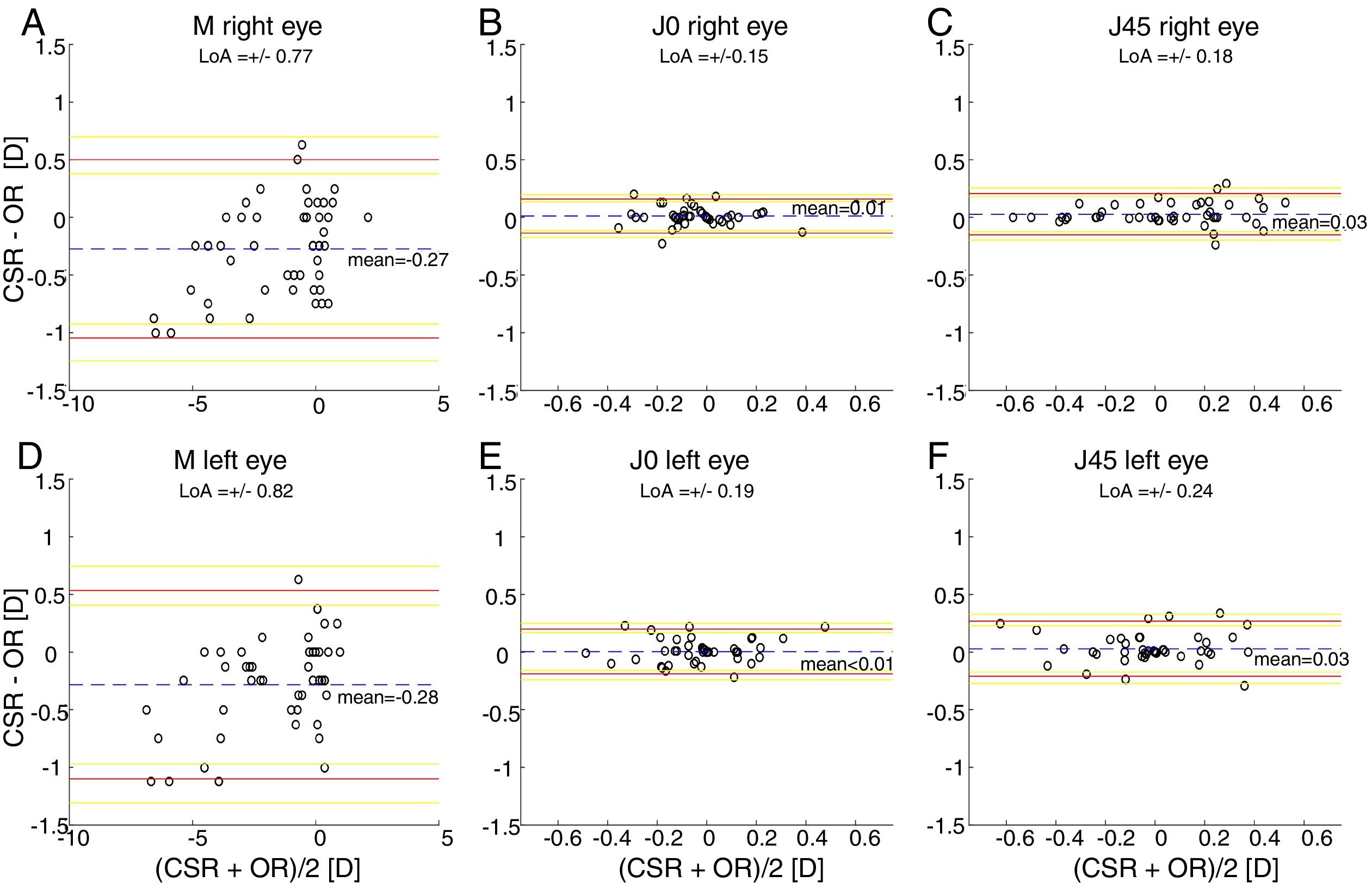
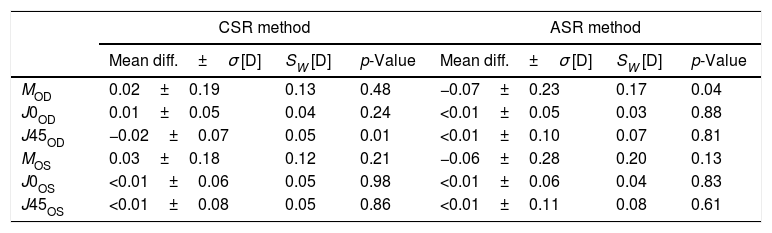
ResultsThe within-subject standard deviations of the power vector components (M, J0, J45) obtained for the right eye are (±0.13, ±0.04, ±0.05)D and (±0.17, ±0.03, ±0.07)D, respectively, for the clinical and the automated subjective refraction methods. The limits of agreement (with the clinical method) for the automated and the objective methods are, respectively (±0.56, ±0.18, ±0.31)D and (±0.77, ±0.15, ±0.18)D. Similar results are obtained for the left eye.
ConclusionsThe proposed automated method is repeatable and more accurate than objective techniques in healthy adults. However, it is not accurate enough to replace the clinical subjective refraction yet and it should be tested in a wider population in terms of age, refraction and different ocular conditions. Despite these important limitations, this method has been shown to be a potentially valuable method to improve the access to primary eye care services in developing countries.
Investigar un nuevo algoritmo para llevar a cabo una refracción automatizada no ciclopéjica en adultos.
MétodosSe midió a cincuenta sujetos sanos dos veces (prueba-reprueba) con el nuevo método de refracción subjetiva automatizado y con al procedimiento de refracción subjetiva clínica convencional. También se midió la refracción objetiva con el autorrefractómetro Grand Seiko WAM-5500. El nuevo método automatizado está inspirado en el algoritmo de bisección de búsqueda de raíces y en las distancias Euclidianasentre los vectores de potencia. Se introdujo el algoritmo en un ordenador, sincronizado a un foróptero motorizado personalizado. La repetibilidad se valoró principalmente mediante la desviación estándar intrasujetos (Sw), evaluándose el acuerdo con los límites de concordancia.
ResultadosLas desviaciones estándar intrasujetos de los componentes del vector de potencia (M, J0, J45) obtenidos para el ojo derecho fueron (±0,13, ±0,04, ±0,05)D y (±0,17, ±0,03, ±0,07)D para los métodos subjetivos de refracción clínica y automatizada, respectivamente. Los límites de concordancia (con el método clínico) para los métodos automatizado y objetivo fueron, respectivamente, (±0,56, ±0,18, ±0,31)D y (±0,77, ±0,15, ±0,18) D. Se obtuvieron resultados similares para el ojo izquierdo.
ConclusionesEl método automatizado propuesto es repetible y más preciso que las técnicas objetivas en adultos sanos. Sin embargo, no es lo suficientemente preciso para sustituir aún a la refracción subjetiva clínica, y debería probarse en una población más amplia en términos de edad, refracción y situaciones oculares diferentes. A pesar de estas importantes limitaciones, este método podrá ser valioso a la hora de mejorar el acceso a los servicios de atención primaria ocular en países en desarrollo.
According to the most recent estimates from the World Health Organization (WHO), the uncorrected refractive error is the main cause of visual impairment, affecting 43% of the global population.1 The largest prevalence of visual impairment is found in developing countries, where one of the leading causes for uncorrected refractive error is the insufficient eye care personnel and massive imbalance in the distribution of eye care services in these countries.2,3 Automated and portable technology capable of performing accurate non-cycloplegic refractions could help to reduce this problem.
The refraction of the human eye can be obtained both objectively and subjectively. Objective refraction measurements can be currently determined fast and easily with autorefractometers and wavefront aberrometers and they are often used as a starting point for conventional subjective refraction.4–6 Several studies have reported limits of agreement between autorefractometers and subjective refraction in the range of ±0.75D to ±1.24D.5,7–9 Analogously, most of the reported limits of agreement between wavefront sensors and subjective refraction are in the range of ±0.56D to ±1.29D.10–13 The information given by wavefront sensors in the form of Zernike coefficients can be summarized in single-value optical quality metrics14 that can be computationally optimized to find an objective refraction that best predicts subjective refraction.15 There are two main wavefront refraction metrics categories, the pupil-plane and the image-plane metrics, being the latter ones much more computationally intensive. In both categories there exist accurate metrics in predicting subjective refraction (e.g., the Visual Strehl ratio calculated from the optical transfer function, VSOTF).14–17
However, prescribing from objective findings alone achieves limited patient satisfaction and visual acuity does not improve sufficiently in some individuals.5,11,18 In particular, non-cycloplegic objective refraction can be significantly less accurate in infants and young adults due to their over-accommodation during the objective refraction measurements.19,20 Fogging with plus lenses is an alternative to cycloplegia to avoid or minimize accommodation during autorefraction or wavefront sensing. A fogging lens of +2.00D has been shown to relax accommodation in a similar way to cycloplegia in young adults,21 which supports the fact that refraction is mainly driven by the central part of the pupil even in the presence of spherical aberration or a larger pupil diameter.22
Subjective refraction is considered the gold standard of refraction.23 It is based on comparing different lenses (i.e., spherical and cylindrical lenses) and measuring changes in visual acuity to arrive at the lens combination that maximizes it.24 In contrast to objective refraction, subjective refraction relies on the response of the patient and on the examiner's skills. These two factors may be the reason why some authors found more variability in subjective refraction than in objective refraction outcomes25,26 Although Rosenfield and Chiu27 found no meaningful differences in variability, they obtained mean standard deviations for the subjective and objective techniques of ±0.15D and ±0.14D, respectively.
Despite the goal of subjective refraction seems simple, it is a challenging procedure especially when not using cycloplegia to minimize accommodation artefacts in non-presbyopes, who may sometimes require to accommodate to achieve the maximum visual acuity.23 This is the case of pseudomyopes28 or latent hyperopes.29 Pseudomyopes is a term used for negative subjective spherical refractions whereas latent hyperopes is a term for positive subjective refractions in the presence of excessive accommodation.30 In both situations a cycloplegic refraction to obtain the full refractive error is recommended and spectacle prescription should be based on careful consideration of the patient's individual visual needs.28–30
Recently, new technologies have appeared with the aim of approaching eye's refraction to general population in a more affordable way10,12,31 although none of them include the patient's psychophysical response, which limits their applicability for screening purposes or spectacles prescription. Having all this in mind, the purpose of this study is not only to propose, but implement and test an algorithm to perform an automated non-cycloplegic refraction in adults.
MethodsInstrumentThe proposed method to obtain the subjective refraction of the eye can be generalized and implemented in any optical system capable of changing the sphero-cylindrical refraction of both eyes according to the patient's psychophysical response. For a proof of concept of the algorithm a manual phoropter was converted into a motorized system. A commercial manual phoropter (VT-10, Topcon Co. Ltd., Japan) was partially disassembled and 8 motors (4 for each eye) were introduced to control the sphere power, cylinder power, cylinder orientation and the occluder of each eye independently. All motors were connected to drivers which in turn were connected to a computer with a USB cable and controlled via Matlab R2015b (MathWorks, Inc., USA). A display connected to the computer was placed at 6-meter distance from the subject and was used as the stimulus display. We used the monitor Philips 246V with 24 inches and 1920×1080 pixel resolution, which could display optotypes from 1.5 to less than −0.3 logMAR (from 20/632 to 20/10 Snellen acuity). A wireless keyboard was used by the subjects to provide an answer to the psychophysical tasks implemented in the new algorithm that are explained in detail in the next section. The setup is shown in Fig. 1 and a graphical example of the psychophysical tasks is shown in Fig. 2.
Picture of the clinical setting with the custom-made motorized phoropter. Four motors were attached in the anterior surface and 4 motors were attached in the posterior surface of the phoropter. Motors are connected to the drivers and a USB cable connects the drivers to the control PC. The wireless keyboard is used by the observer to respond (e.g., to respond to stimulus orientation: up, down, left or right).
The automated subjective refraction algorithm receives as an input the starting point of refraction for each eye, which in this study corresponded to the measures obtained with the WAM-5500 autorefractometer or the current spectacle prescription. The WAM-5500 is an open-field instrument that projects a target through a 2.3mm diameter annulus onto the retina and determines refraction by measuring size and shape after reflection from the retina through the optics of the eye.5 Previous studies showed that the WAM-5500 can accurately measure the on-axis refractive state of the eye,5,21,32 although some authors have reported a small hyperopic bias compared to subjective refraction,5,32 which could suggest a good control of instrumental accommodation.
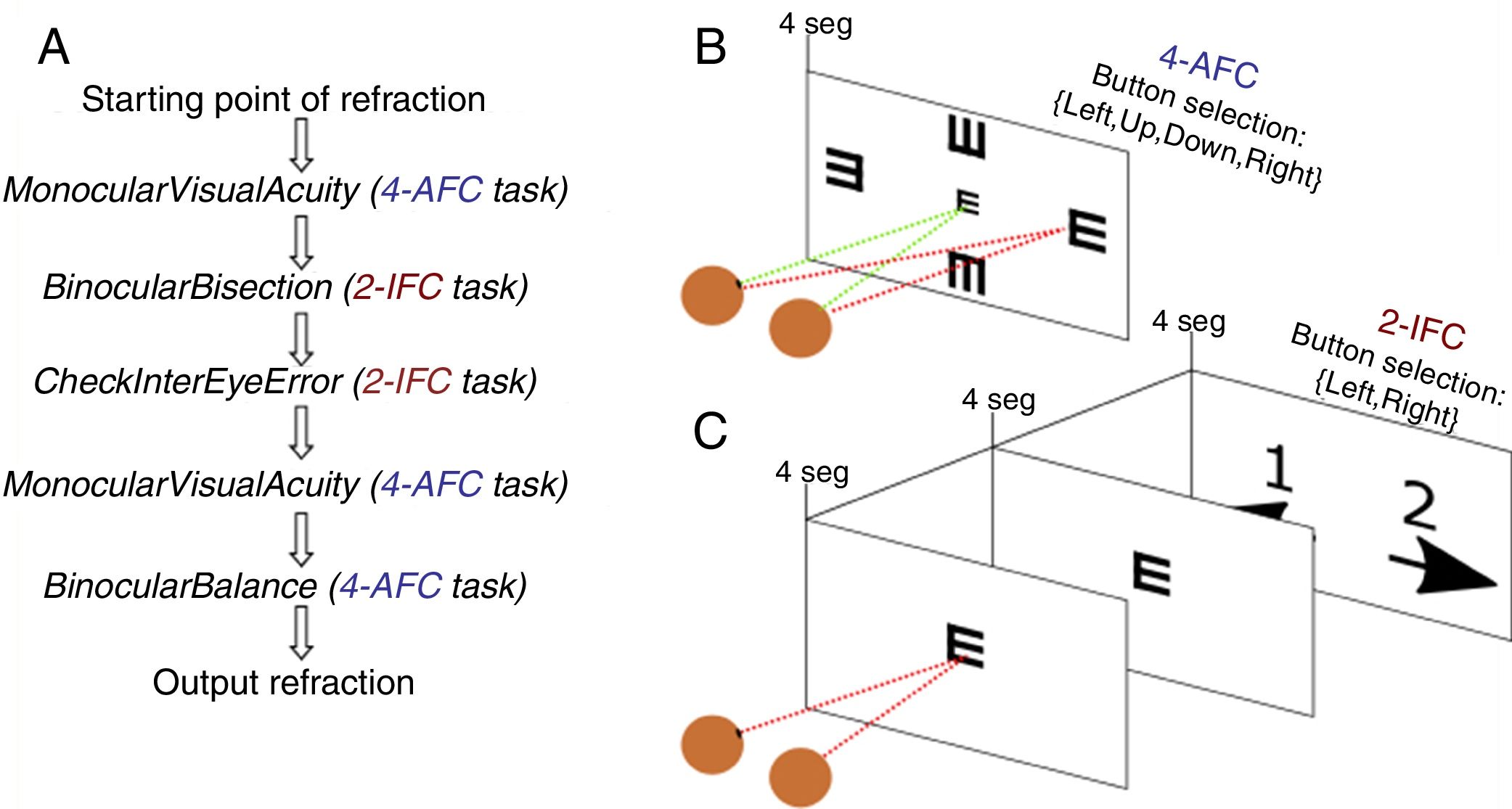
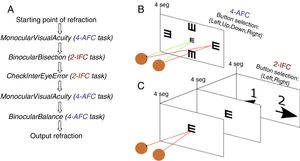
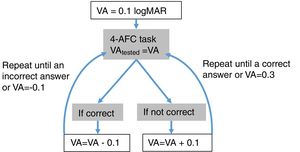
Once the starting point of refraction is obtained, the algorithm goes through a sequence of 5 functions shown in Fig. 2 and detailed below. Each of these functions implements either a 4-alternative force choice task (4-AFC) or a 2-interval force choice task (2-IFC). On the one hand, the 4-AFC task tests the subjects’ visual acuity as follows: a black Snellen optotype is displayed at certain visual acuity and the subject is asked to select the correct orientation of the letter by pressing the arrows of a computer keyboard (i.e., up, down, left, right). This process is repeated 3 times to reduce the guess rate while the orientation of the Snellen ‘E’ randomly changes each time. On the other hand, the 2-IFC task tests which of the two images is clearest. For example, a black Snellen optotype is shown during 4s to the subjects, while they are looking through the phoropter configured according to a certain sphero-cylindrical refraction, which is then changed and the same Snellen optotype is again shown during 4s with another given refraction. The decision to present a certain refraction firstly or secondly is randomized.
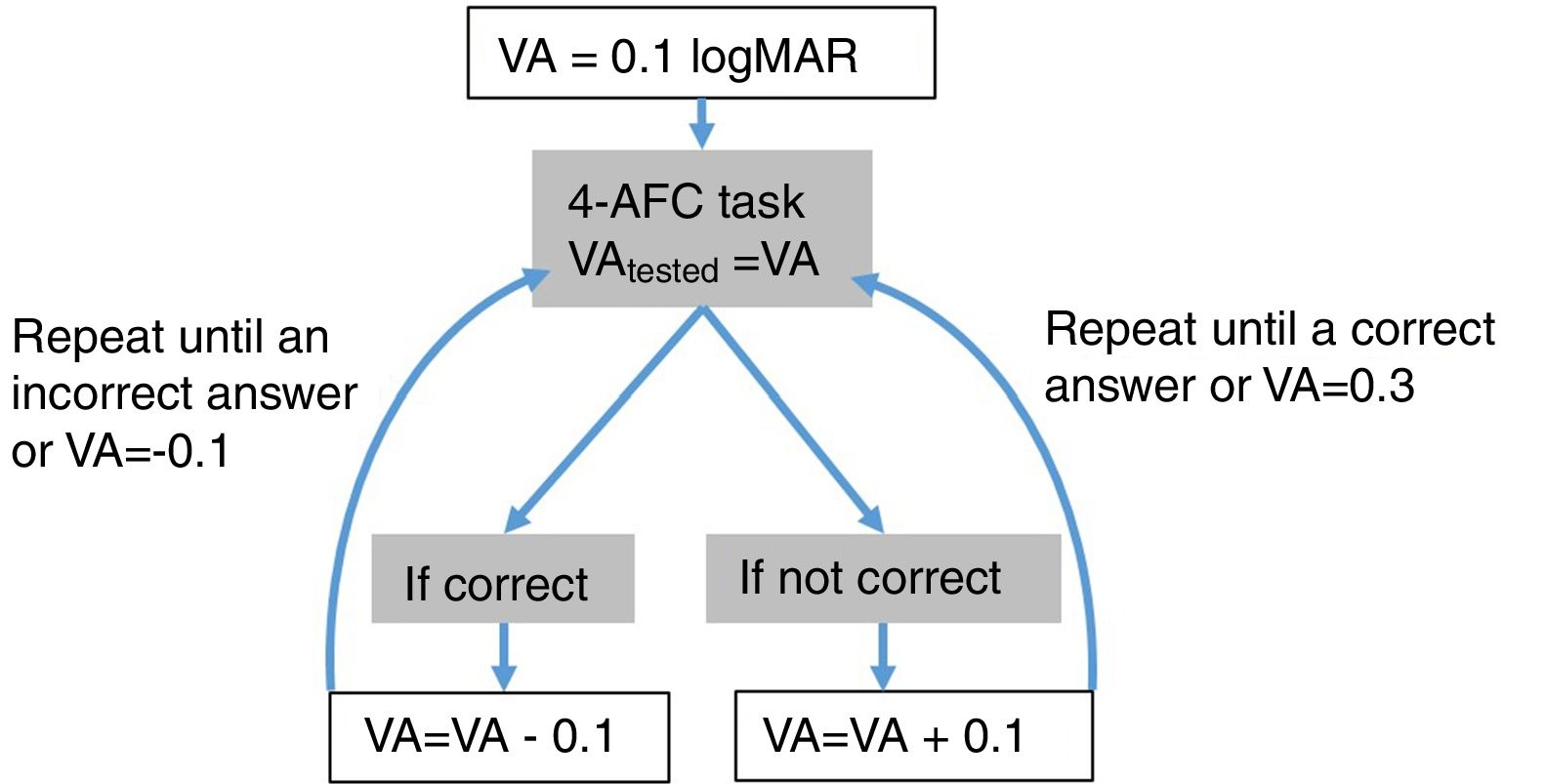
Step 1: MonocularVisualAcuity functionThis function receives as an input 6 values: the sphere, cylinder and axis values of the right and left eye of the starting point of refraction. This function tests the monocular visual acuity of each eye in a four-alternative force-choice task (4-AFC) as shown in Fig. 2B and Fig. 3. For example, if the observer selects 2 out of the 3 times correctly, the optotype size is decreased in steps of 0.1logMAR, otherwise the optotype size is increased in steps of 0.1logMAR until the observer reports 2 out of the 3 orientations correctly. By default, the first visual acuity that is tested is 0.1logMAR.
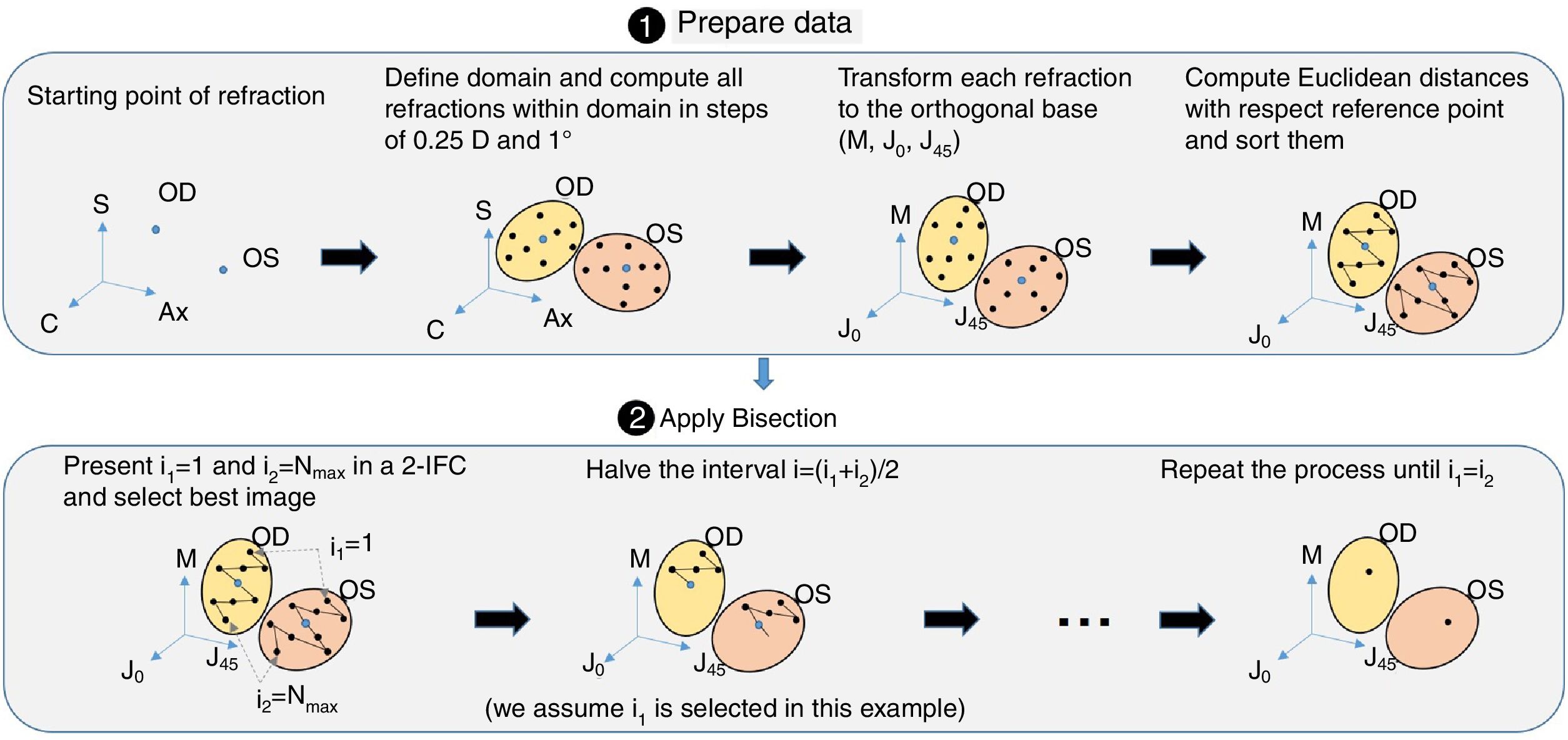
Step 2: BinocularBisection functionThis function receives as input the starting point of refraction for each eye and the monocular visual acuities obtained in the previous function. BinocularBisection starts setting a range of refractions which assumedly comprise the final subjective refraction and over which the algorithm will test the subject's blur perception. The algorithm considers a range of values of the sphere that goes from −0.50 to +1.50D with respect the input sphere. Since some autorefractometers and wavefront sensors tend to give more myopic estimates of subjective refraction,7,11 a longer positive range than a negative one increases the odds to find the optimum subjective refraction. In the case the input sphere corresponds to the current spectacle prescription, it would not be necessary to have such an asymmetric range but in fact, it strengthens a more positive power which is consistent with the end-point criterion of subjective refraction23: maximum plus power with best visual acuity.
Regarding the cylinder power, the algorithm considers a range that starts at the input cylinder power and spans 1.0 D. For axis orientation, the algorithm does not consider any set of different possible axis orientations. It is important to take into account that both cylinder and axis are theoretically bounded quantities, i.e., the axis range is limited to 179° and the cylinder can range from any negative value up to 0D (considering that all input refractions are in negative cylinder notation). The arbitrary decisions of these ranges can limit the accuracy of the algorithm significantly (specially the fact of not considering any change in axis orientation). To consider a set of different axis orientations or to include larger spherical and cylindrical ranges is possible at the cost of efficiency. Our initial implementation is based on multiple previous pilot studies which sought the best balance between efficiency and accuracy.
Next, all the generated sphero-cylindrical refractions for each eye are transformed into power vector notation33 (M, J0 and J45) using Eqs. (1)–(3). This transformation allows algebraic operations on the eye's refraction in an orthogonal 3-D base (M, J0 and J45). Consequently, even if the three variables sphere, cylinder and axis are not independent of each other, they become theoretically independent when transformed into M, J0 and J45.
The next step is to compute for each eye all the Euclidean distances (ED) between all the generated refractions (Mi, J0i, J45i, for i=1,…,Nref) and the most negative refraction (M1, J01, J451) as follows:
Notice that the most negative refraction is the one with the smallest spherical equivalent (M). Next, all the generated refractions are sorted in ascending order of Euclidean distances and a two-interval force-choice task (2-IFC) is performed based on the mathematical root finding bisection algorithm: an interval is repeatedly halved and in each partition the subinterval in which the best refraction is considered to lie is selected as the next interval. A diagram of this step's algorithm is shown in Fig. 4.
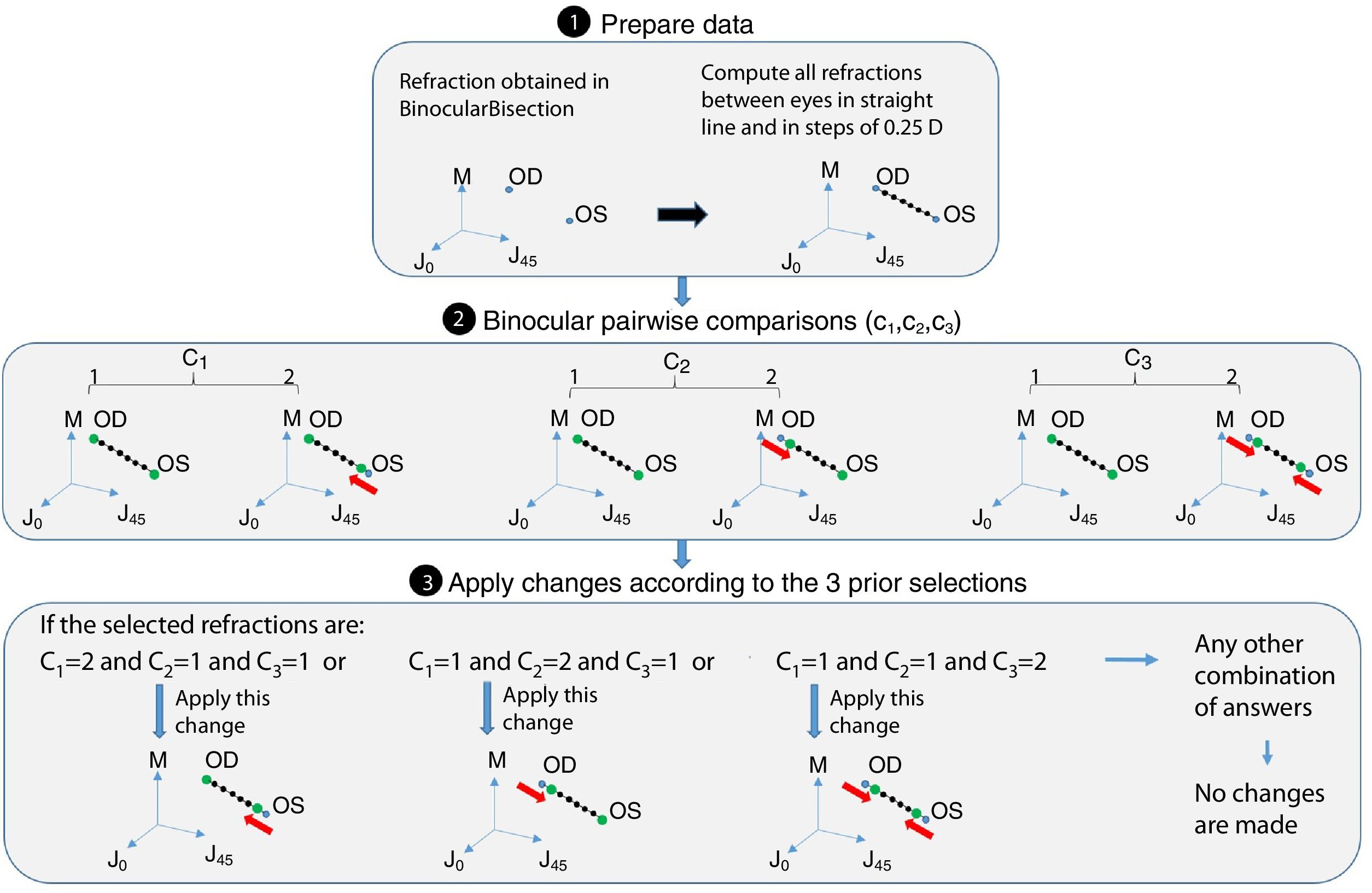
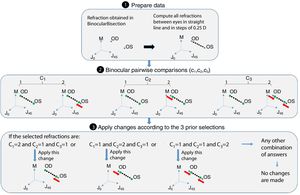
Step 3: CheckInterEyeError functionThis function receives as input the output of the BinocularBisection function. This function aims to reduce the inter-eye measurement error that may come from the starting point of refraction when there is a difference in refraction (either in cylinder or sphere) of 0.75D or more between the right and left eye's refraction. If differences between right and left eye's sphere or cylinder are less than 0.75D the algorithm jumps directly to the next function without making any change. If the differences are greater or equal than 0.75D the algorithm follows the diagram flow of Fig. 5.
Step 4: BinocularBalance functionThis function receives as input the values of sphere, cylinder and axis of both eyes obtained in BinocularBisection or CheckInterEyeError function and the values of monocular visual acuity obtained in the previous function. The aim of this function is to find the maximum plus power with the same visual acuity obtained in the previous function. It is added an arbitrary value based on previous pilot studies of +0.50D to the sphere of the right and left eye. Then, the 4-AFC task is performed binocularly. If the observer answers incorrectly in 2 out of the 3 times, the sphere is decreased 0.25D in both eyes, otherwise the algorithm ends and the final subjective refraction is the last refraction tested.
Examination protocolThe study was approved by the Ethics Committee of Hospital Mutua de Terrassa (Terrassa, Spain). The study follows the tenets of the Declaration of Helsinki and all subjects gave informed written consent.
Non-cycloplegic binocular subjective refraction was obtained twice in 50 healthy adults (none of which suffered from ocular disease) with the new automated method and with the conventional clinical subjective refraction procedure performed in a manual phoropter. All measurements were obtained in two sessions within 1 week. The objective refraction was obtained with the WAM-5500 (Grand Seiko Co. Ltd., Japan) and was used as starting point of refraction for the clinical subjective refractions. One clinician performed all subjective refractions and was blinded to the refraction results obtained with the automated method. The clinician was a graduated Spanish optometrist with 3 years of working experience and strictly adhered to a refraction protocol of maximum plus power for best visual acuity. All clinical subjective refractions followed a monocular refraction plus biocular and binocular balance. Cylinder and axis orientation were refined with Jackson cross-cylinders. The duochrome test was not used in any case and all refractions were performed under the same room lighting conditions.
Data analysisStatistical significance was set at 0.05 and the statistical analysis was performed using MATLAB R2015b (MathWorks, Inc., USA). Normality of each variable was verified with the Shapiro–Wilk test. Repeatability of the new method and repeatability of the clinician were analyzed by means of the within-subject standard deviation (Sw). The repeatability of the autorefraction (i.e., Grand Seiko WAM-5500) has been widely reported.5,10,34 Agreement between the automated and the clinical subjective refraction was assessed with Bland and Altman plots for each eye and parameter, as well as the agreement between autorefraction and the clinical subjective refraction. Additionally, paired t-tests were applied for repeatability analysis and repeated measures ANOVA were applied for the agreement analysis between the three methods. Statistical power was assessed with the free open-source program G*Power 3.0.10. A pilot study with 25 subjects was conducted to calculate the sample size needed for a statistical power of 0.95 and it resulted in 40 subjects.
ResultsThe mean age±standard deviation of the 50 observers was 30±8 years (20–57 years) with a mean spherical equivalent refractive error of −1.74±2.28 (−7.25 to 2.13)D and with mean corrected visual acuity of 20/17±20/23.5 (20/32.5 to 20/16). The starting point of refraction for the automated method was the most current spectacle prescription in 36% of the subjects. On average, the new proposed method took 4min and 16s (±44s) and the conventional standard procedure took 4min and 37s (±50s). Note that both time computations do not account for the time spent obtaining the starting point of refraction (e.g., autorefraction) or current spectacle prescription. The time difference was statistically significant (paired sample t-test, p=0.02).
Repeatability resultsThe mean difference±standard deviation (σ) between both sessions (test–retest), the within-subject standard deviation (SW) and the p-values obtained with the paired sample t-test are shown in Table 1 for each eye, parameter and method (i.e., automated subjective refraction and clinical subjective refraction).
Repeatability (test–retest) for each eye, parameter and method.
| CSR method | ASR method | |||||
|---|---|---|---|---|---|---|
| Mean diff.±σ [D] | SW [D] | p-Value | Mean diff.±σ [D] | SW [D] | p-Value | |
| MOD | 0.02±0.19 | 0.13 | 0.48 | −0.07±0.23 | 0.17 | 0.04 |
| J0OD | 0.01±0.05 | 0.04 | 0.24 | <0.01±0.05 | 0.03 | 0.88 |
| J45OD | −0.02±0.07 | 0.05 | 0.01 | <0.01±0.10 | 0.07 | 0.81 |
| MOS | 0.03±0.18 | 0.12 | 0.21 | −0.06±0.28 | 0.20 | 0.13 |
| J0OS | <0.01±0.06 | 0.05 | 0.98 | <0.01±0.06 | 0.04 | 0.83 |
| J45OS | <0.01±0.08 | 0.05 | 0.86 | <0.01±0.11 | 0.08 | 0.61 |
CSR: clinical subjective refraction; ASR: automated subjective refraction; Diff.: difference; σ: standard deviation; SW: within-subject standard deviation.
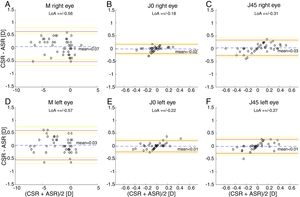
The Bland and Altman plots comparing the automated subjective refraction with the clinical subjective refraction for each eye and parameter are shown in Fig. 6. Analogously, the Bland and Altman plots comparing between autorefraction and the clinical subjective refraction is shown in Fig. 7. The results of the repeated measures ANOVA considering the three methods and applied to the right eye parameters are: F=26.46, p<0.01 for M; F=2.67, p=0.07 for J0; and F=1.37, p=0.26 for J45. Analogously, the results for the left eye are: F=1.74, p<0.01 for M; F=0.14, p=0.87 for J0; and F=2.05, p=0.14 for J45.
Bland and Altman plots. (A, B, C) Right eye data. (D, E, F) Left eye data. The top and bottom red lines indicate the superior and inferior 95% limits of agreement (LoA), respectively. The yellow lines indicate the superior and inferior 95% confidence interval for each limit of agreement. The dashed, blue lines indicate the mean difference. CSR: clinical subjective refraction; ASR: automated subjective refraction.
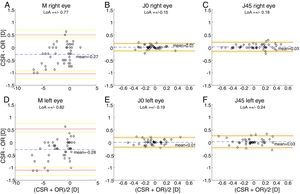
Bland and Altman plots. (A, B, C) right eye data. (D, E, F) left eye data. The top and bottom red lines indicate the superior and inferior 95% limits of agreement (LoA), respectively. The yellow lines indicate the superior and inferior 95% confidence interval for each limit of agreement. The dashed, blue lines indicate the mean difference. CSR: clinical subjective refraction; OR: objective refraction (Grand Seiko WAM-5500).
Only the repeated measures ANOVA applied to the spherical equivalent of both eyes results in statistically significant differences among methods. The Bonferroni post hoc test for the right and left eye shows that differences between autorefraction and clinical subjective refraction are statistically significant (p<0.01) as well as the differences between autorefraction and automated subjective refraction (p<0.01).
DiscussionA new method to perform non-cycloplegic binocular subjective refraction without the support of a clinician was investigated. Repeatability (test–retest) and agreement of this new method in relation to the conventional clinical procedure was assessed in 50 subjects. A total of 6 variables were analyzed: the power vectors components (M, J0 and J45) of both eyes.
Repeatability analysisThe within-subject standard deviations found for the automated method are comparable to those found for the clinical subjective refraction for all three components (M, J0 and J45). In all cases we obtained within-subject standard deviations below 0.25D, which is the limit of clinical significance. The worst-case within-subject standard deviation (Sw) was ±0.20D for the spherical equivalent M and for the automated subjective refraction (Table 1, OS). It is consistent with previous studies where standard deviations between ±0.15D and ±0.38D were reported between and within clinicians.25,27,35,36 Autorefractors and wavefront sensors are, in general, more repeatable than subjective refraction since they do not depend on the patient's response or the clinician's skills. For instance, Pesudovs et al.25 compared the repeatability (test–retest) of two well-known autorefractors (Topcon KR-8000, Nidek AR-800) and found standard deviations for the spherical equivalent of ±0.04D and ±0.07D, respectively. Otero et al.37 analyzed the repeatability (averaging 3 measurements) of a wavefront sensor (AOVA, Voptica S.L., Spain) and obtained within-subject standard deviations for the sphere of ±0.17D.
Agreement analysisFor the spherical equivalent M, the automated method showed both smaller limits of agreement (±0.57D) and a smaller mean bias (0.05D) than the objective method (±0.80D and −0.28D respectively). Moreover, the ANOVA post hoc analysis highlighted no statistically significant differences between the reference method (clinical subjective refraction) and the automated refraction, while statistical differences were found when compared to objective refraction. Regarding the cylinder, the limits of agreement obtained for the automated and the objective refraction can be considered equal and no statistically significant differences were found in any case. Thus, on average the automated refraction improves the agreement with the gold standard in comparison with objective refraction and its limits of agreement are close to the limit (±0.50D) suggested by Rosenfield and Chiu27 as the minimum significant shift in refraction status.
In comparison with other studies, on the one hand there are 3 relatively recent studies34,38,39 that compared the agreement of an automated subjective refraction methods with the conventional clinical subjective refraction. Two of them used the same device (Topcon BV-1000, no longer commercially available) and they reported limits of agreement for the spherical equivalent of ±0.69D and ±0.82D.38,39 The third study was performed in our lab, the automated method was implemented on a stereoscopic virtual reality system and limits of agreement of ±0.88D were obtained for the spherical equivalent.34 On the other hand, Sheppard et al.5 compared autorefractor readings of the WAM-5500 (Grand Seiko Ltd., Japan) with the subjective refraction and found limits of agreement for the spherical equivalent of ±0.75D. In addition, older studies7,8 that compared autorefractor measurements (without cycloplegia) with subjective refraction found limits of agreement around ±0.95D. In summary, an accurate refraction device/method should not only have a small mean bias (<0.25D) but also small limits of agreement (<±0.50D). Up to date, neither the objective nor automated refraction methods existing in the literature have shown limits of agreement below 0.50D (not even in healthy subjects).
Limitations of the automated methodOur results suggest that the new proposed method is reasonably equivalent to the conventional clinical subjective refraction in time duration, accuracy and precision. It incorporates two important novel factors: it does not require clinician support and it has better accuracy than most objective refractometers and wavefront sensors. However, this new method still needs some improvements before it can be widely used.
In terms of accommodation control, the automated method does not control it. Especially in the BinocularBisection function where observers simply chose the clearest image in each pair of refractions regardless the chosen refraction could make subjects accommodate. However, our results suggest that the automated method was not significantly affected by accommodation artefacts which is likely due to: (1) only healthy adults (without accommodative anomalies) were tested; (2) the short negative ranges that were established in the BinocularBisection function limited the potential negative shift; and (3) the starting point of refraction was reasonably accurate in most of the cases. Thus, the results did not allow to conclude anything about the performance of the algorithm in children, people with ocular pathologies or accommodative anomalies. In these cases a cycloplegic refraction with a professional is advised.
Another potential limitation of this study is the choice of Euclidean distance as a single-value optical quality metric of the eye. This metric was chosen because its dependency on low order aberration terms only, but it is well-known that there exist other (more elaborated) metrics for which the algorithm may have a much better performance.14–17 Further studies may investigate on embedding the wavefront objective refraction in the automated algorithm, which may significantly improve the accuracy of the BinocularBisection function.
In terms of the cylinder determination, an unexpected systematic linear error in the Bland and Altman plots for the J0 and J45 in both eyes was observed (Fig. 6B, C, E and F). We cannot entirely explain the source of these errors and interestingly, other studies that compared a handheld wavefront sensor to subjective refraction also reported such systematic errors.10,12 It is also an important decision to set the axis orientation as a fixed parameter. This was chosen for efficiency and considering the following: the precision of cylinder axes determined subjective is approximately around ±10°27; and between 80% and 95% of the cylinder axes determined with an autorefractor are within 20° (or less) of those found subjectively.5,7,18 Thus, while in most cases we found that the axis determined objectively is within clinically acceptable values, it might not be appropriate for some subjects and the new proposed method should be able to effectively include them in future improvements (for instance, by introducing some pairwise comparisons of refractions with different cylinder orientations in a 2-IFC task).
Overall, it has been shown that the automated method is precise enough and more accurate than autorefraction and wavefront sensing in healthy adults. It is the authors’ opinion that the long term goal of both objective and automated refraction methods aim to replace the clinical subjective refraction for two main reasons: (1) the great interest of the ophthalmic industry on objective and automated technologies for machine learning and tele-medicine applications40 and (2) to bring primary eye care services to remote (under-developed) areas of the world. This latter point is especially important in developing countries where this automated method in conjunction with appropriate lens-based technologies could significantly contribute to overcome the lack of primary eye care services.2,3 Given that both objective and subjective methods have not proven to be accurate enough to fully replace the clinician yet, these new methods are still far from being adopted widely by the optometric and ophthalmologic community in the short term. Therefore, these technologies should be limited as screening tools only except in those regions where no other alternatives are available (i.e., in developing countries with limited access to vision care professionals).
Finally, we believe that another possible advantage of the algorithm presented in this study is the possibility to adjust all the free parameters of the method individually when optimization of these parameters can be adapted to, for instance, the subjects’ age and prior refraction or initial visual acuity. Consequently, the new automated method can potentially offer a more flexible and controlled way of performing subjective refraction.
ConclusionsThe first implementation of the algorithm has shown a potential novel method of performing non-cycloplegic subjective refraction in adults without clinician support. Although it presents some limitations that warrant further research and it still should be tested in a wider population in terms of age, refraction and different ocular conditions, this method can contribute to improve the access to primary eye care services in developing countries.
FundingThis research was supported by the Spanish Ministry of Economy and Competitiveness under grants DPI2014-56850-R and RTC-2014-2345-1 and Davalor Salud, S.L (Spain).
Conflict of interestCO and JP have pending intellectual proprietary interest in the methods presented in this study (patent pending).
The authors would like to thank Rocío García for her support during data collection.