To study how spherical High-Order Aberration (HOA), astigmatism levels (-0.75 D and -1.25 D), and optotype type (dot pattern vs. letter row) influence patients’ responses in identifying the cylinder axis orientation with the Jackson Cross Cylinder Technique (JCCT).
MethodsNumerical simulations of retinal images corresponding to JCCT procedures were conducted and evaluated by 40 subjects. In order to do this, synthetic aberrometric profiles with and without HOAs (4th-order and 6th-order spherical aberrations) and two different astigmatism levels were generated from different Jackson Cross Cylinder axis positions and flips. The variable under study was the percentage of correct responses (hits) during each flip of the cross-cylinder lens. Statistical significance was assessed through confidence intervals overlapping evaluation.
ResultsTo achieve 90 % accuracy, the JCCT should begin by deviating >7.5° from the subject's astigmatism axis without spherical HOA and by >15° with them. The magnitude of astigmatism had minor relevance. The dot pattern was more accurate than the letters without HOAs; however, 72.5 % of observers considered that letter optotypes simplify the blur discrimination task.
ConclusionsAccording to our simulation experiment for astigmatic axis selection with JCCT, the presence of spherical HOAs significantly impacts the accuracy of patient responses. The type of optotype and the magnitude of astigmatism did not exhibit a clear relationship with accuracy, except in the case of the dot pattern optotype in the absence of HOAs. Under these conditions, the dot pattern achieved the highest rate of accurate responses.
Monocular subjective refraction is a popular technique used to determine the combination of spherical and cylindrical lenses that provides the most positive lens for achieving maximum Visual Acuity (VA).1 However, there are subjects with refractive errors for which no spherical-cylindrical compensation can achieve good visual quality, even in the absence of amblyopia. This type of refractive defect is traditionally named as irregular astigmatism.2 The refractive power for irregular astigmatism varies not only from one meridian to another but also within the same meridian and/or across the aperture's transverse coordinate. In contrast, regular astigmatism is a refractive defect that can be effectively corrected using spherical-cylindrical lenses.
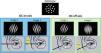
The wavefront of an ocular system affected by regular astigmatism typically presents two principal perpendicular meridians, resulting in a focal irradiance distribution known as Sturm's conoid. Sturm's conoid is determined by two linear focal distributions and an intermediate region named Circle of Least Confusion (CLC). Generally, the focal interval in cases of irregular astigmatism lacks this symmetry (see Fig. 1).
Distribution of Sturm's conoid in optical systems. At the top, it is shown a set of point spread energy distributions for different image distances; the system's wavefront aberrations correspond to low-order astigmatism and varying defocus values. At the bottom, an analogous representation for a system with irregular astigmatism. In this case, the wavefront combines the same defocus and astigmatism values as above, along with a component of 4th-order spherical aberration.
Currently, technology aimed at characterizing ocular wavefront aberration allows for its description using Zernike coefficients, as proposed by Mahajan.3 This technology facilitates the specific characterization of irregular astigmatism based on the contribution of Zernike polynomials of radial order >2, which are classified as high-order aberrations. Based on this characterization, compensation for irregular astigmatisms can be achieved through ablation patterns in refractive surgery4 or through contact lenses designed with a height profile that generates the appropriate conjugate optical wavefront.5
Several techniques for monocular subjective refraction are employed to determine the orientation and power of the cylindrical component in the refractive compensation of regular astigmatism.6-8 Among these, the Jackson Cross Cylinder Technique (JCCT)9 is the most widely used in clinical practice, even with treatment that might be based on the induction of HOAs.10
The JCCT is a subjective procedure involving the use of a crossed cylinder lens mounted in a handle or a rotating holder, a crossed cylinder lens is an astigmatic lens with null spherical equivalent which can be regarded as two cylindrical lenses of equal power and opposite signs placed perpendicular to each other. In this technique, the patient is asked to discriminate between two image qualities corresponding to two different positions of the Jackson Cross Cylinder (JCC) (Image 1 or Image 2, in Fig. 2). When the patient prefers one image, it indicates that the axis of the JCC lens's negative cylinder is closest to the ocular astigmatism axis. The JCC symmetric axis (where the handle use to be placed) is then rotated accordingly, and the process continues. Then, if the patient reports no preference between both images, this orientation is set as the correct axis for ocular astigmatism.11 Once the cylinder axis is determined, the cylinder power is adjusted using a similar procedure.
Retinal image simulations developed according to the JCCT. The blue dashed line indicates the orientation of the patient's astigmatism axis, while the red and white lines represent the orientation of the negative and positive cylinder axes of the JCC lens, respectively. On the left side of the figure, the JCC lens is flipped while keeping its symmetry axis aligned with the ocular astigmatism (on-axis); on the right, an analogous simulation for an off-axis situation of the JCC lens is shown.
The operational principle of the JCCT is based on the optical effect of the flipped lens on Sturm's conoid for different orientations relative to the actual ocular astigmatism axis. Therefore, in the presence of High-Order Aberrations (HOAs) that cause irregular astigmatisms, the JCCT may not be suitable, potentially leading to errors in cylindrical compensation prescriptions.12
Research on the factors affecting the performance of the JCCT goes back several years, making it difficult to find recent studies on the subject. Factors that may contribute to erroneous prescriptions and must be carefully considered include the refractive state at the onset of the JCCT,13-15 the influence of the test used,16,17 the interaction between the optometrist and the patient and the difficulty in understanding certain instructions during the test. Moreover, the interaction among all the influencing factors makes it difficult to draw clear conclusions about the isolated influence of each one.
Retinal image simulation has shown as a useful tool to understand subjective refraction responses18,19 or expected visual quality with multifocal lenses20 surgical refractive procedures21 and pathological conditions. Experiments where different external subjects judge the same images can be conducted with minimal equipment, thanks to retinal image simulation. In that sense, with a suitable experiment, the role of different subjective criteria for assessing image quality can be revealed.
This study aimed to investigate the influence of optotype, aberrometric profile and astigmatism on patient's responses during the JCCT axis orientation procedure. To achieve this, numerical image simulations using Fourier filtering were employed to develop controlled subjective experiments. The characterization of the subject's responses included the use of two different optotypes (a dot pattern and a row of letters), two levels of astigmatism (0.75 and 1.25 D), and different levels of 4th-order and 6th-order spherical aberrations. The responses were evaluated for both on-axis and several off-axis settings of the JCC lens.
Material and methodsSubjectsForty observers, recruited from the University of Zaragoza, participated in this study. The research adhered to the tenets of the Declaration of Helsinki and was approved by the Ethics Committee for Clinical Research of Aragon (CEICA). After providing a detailed explanation of the study's nature and potential consequences, signed informed consent was obtained from all participants. The inclusion criteria were as follows: subjective refractive astigmatism of less than −0.50 D, best-corrected binocular VA of at least +0.1 logMAR and absence of: any current ocular pathology, history of prior ocular surgery, strabismus, nystagmus, or amblyopia.
Retinal image simulationRetinal image simulations were performed using standard Fourier filtering techniques. A comprehensive description of the methodology for computing the simulated images is provided elsewhere.14 Two different optotypes were used as visual object: a single row of letters and a dot pattern. A ± 0.25 D JCC lens was used to perform the tests.
Simulated retinal images were generated from six synthetic aberrometric wavefronts (6 mm pupil diameter) named as: A_075, A_125, B_075, B_125, C_075, C_125 (futher descriptions provided in Table 1). All aberrated wavefronts shared the same second order Zernike defocus coeficient (Z20= −0.282 µm). Wavefronts A_075 and A_125 represented aberrometric profiles without HOAs but with different levels of astigmatism. Specifically, A_075 exhibited −0.75 D of low-order astigmatism (LOAst) at 0° (Z22= − 0.689 µm), while A_125 presented −1.25 D of LOAst at the same axis (Z22= −1.148 µm). The induced astigmatism axis expressed in minus cylinder form is at 180°.
Refraction and Zernike aberration coefficients for each profile with a 6.00 mm pupil diameter.
Z20 represent defocus, Z22 astigmatism at 0°/180°, Z40 and Z60 correspond to 4th and 6th-order spherical aberrations, respectively.
Wavefronts B_075 and B_125 presented the same typical 4th-order spherical aberration (Z40= +0.200 µm) but differed in their levels of LOAst (−0.75 D and −1.25 D respectively). Finally, C_075 and C_125 exhibited high levels of 4th-order (Z40= +0.395 µm) and 6th-order spherical aberrations (Z60= +0.081 µm) with the same LOAst than others aberrometric profiles.
Low-order coefficients were calculated using the expressions described by Thibos et al.22 to minimize the Root Mean Square (RMS) wavefront error. Given that the spherical dioptric step of a typical phoropter is 0.25 D, the nearest available spherical value was used to approximate the meridional balance state.
For each optotype, aberrometric wavefront profiles and both flipped positions of the JCC lens, a set of gray images was generated for eight different positions of the JCC symmetric axis: 0°, 2.5°, 5°, 7.5°, 10°, 15°, 20° and 30°. Evaluating small, medium, and large angular positions, a more comprehensive estimation can be obtained in cases where determining the cylindrical axis of the manifest refraction is difficult.
This resulted in a total of 96 pairs of retinal image simulations (48 pairs for each optotype). The images had a resolution of 335×335 pixels for the dot pattern and 361×44 pixels for the letter optotype. The line of Sloan optotypes equivalent to a decimal VA of 0.7 (7.14 arcminutes) was used as the original object. Fig. 3 shows a sequence of retinal image simulations for profile A_075, illustrating different axis and flip positions of the JCC lens.
Retinal image simulations for profile A_075, with −0.75 D of LOAst and the induced astigmatism axis expressed in minus cylinder form is at 180°. The JCC symmetric axis is shown aligned with the astigmatism axis (on-axis) and rotated by 2.5°, 5°, 7.5°, 10°, 15°, 20° and 30° relative to the patient's astigmatism axis (off-axis).
The experiment involved presenting pairs of simulated retinal images, which were displayed on a computer monitor with a resolution of 2560×1600 pixels, pixel density of 227 ppi and 500 nits of average luminance. The participants viewed the images binocularly from a fixed distance of 40 cm wearing their refractive correction. No mydriatic or cycloplegic agents were administered during the study.
The result of the convolution of the aberrated point spread function with each original object was magnified on the display with an angular size to facilitate a comfortable comparison by the observers. In particular, the convolved Sloan optotypes were displayed at an angular size of 5.16° (equivalent to 0.02 decimal VA). The full angular size of the aberrated dot optotype subtended 34.96° (with each single dot subtending 4.60°). The luminance of the background surrounding the optotype was 0.08 cd/m².
The observers evaluated pairs of simulated retinal images in a temporal sequence according to the JCCT and were forced to choose among three possible responses: Response1: Image 1 appears better than Image 2; Response2: Image 2 appears better than Image 1; or Response3: There is no preference between them.
For each comparison case, a response was considered correct when it corresponded to the expected outcome for each situation. This means that, when the JCC angular axis position was at 0°, Response3 was considered the correct response. However, for all other JCC angular axis positions evaluated in this study, only the selection of the image generated with the negative cylinder axis of the JCC closest to 0° was considered the correct response. To mitigate potential learning effects, this situation was randomly assigned to Response1 or Response2, depending on the trial.
The experimental protocol was conducted under the supervision of an experienced optometrist (D.G.Y.). Measurements were collected during a single 45-min session. The experimental setup was in a dedicated room space with a constant ambient illuminance of 375 lux.
Moreover, at the end of the test, the participants were asked to provide a subjective assessment to determine which optotype, either the dot pattern or the row of letters, they found easier to detect.
Data analysisThe variable under study was the percentage of correct responses (hits), and confidence intervals were calculated using the Wilson method with a significance level of p < 0.05.23 Statistically significant differences were considered when there was no overlap between the confidence intervals. The hits percentage was analyzed in relation with aberrometric profile, magnitude of astigmatism, and optotype.
ResultsA total of 40 Caucasian participants with an average age of 21.21 ± 3.49 years (ranging from 18 to 35 years), were included in this study.
Influence of aberrometric profileAn overall analysis of the results, considering both optotypes and astigmatism magnitudes across all JCC orientations and all subjects, reveals that profile A, characterized by the absence of HOAs, achieves an average hit percentage of 86.32 ± 16.54 %. In contrast, profiles B and C, both exhibiting HOAs, demonstrate lower mean hit percentages of 76.48 ± 24.69 % and 73.27 ± 26.05 %, respectively.
Fig. 4 illustrates the average hits percentage based on the JCC orientation for profiles: A_075, B_075 and C_075. For clarity, this figure presents results for a single magnitude of astigmatism (−0.75 D) and a specific optotype (dot pattern). It can be observed that when the JCC axis is aligned parallel to the compensation axis, the hit percentage approximates 80 %. A 2.5° off-axis rotation results in a decrease in the hit percentage for all profiles; however, this decrease is more pronounced in profiles with HOAs (B_075 and C_075) compared to the profile free of HOAs. These differences were statistically significant (highlighted with a bracket and an asterisk symbol).
As the JCC axis is oriented further from the axis of compensation (>2.5° off-axis), an increase in the percentage of correct responses is noted. In these positions, profiles B_075 and C_075 show a lower hits percentage compared to profile A_075, with statistically significant differences between the HOA and non-HOA profiles. However, no statistically significant differences were found between the profiles with HOAs. From 15° to 20° off-axis, the hit percentages across all three profiles become similar, although statistically significant differences persist among the profiles. At 30° off-axis, the hit percentage slightly decreases relative to the 20° off-axis condition, but only in profiles with HOAs.
Influence of the magnitude of astigmatismFig. 5 illustrates the hits percentage as a function of astigmatism magnitude for all profiles, using the dot pattern. Subfigures 5a), 5b), and 5c) show the results for profiles A, B and C, respectively.
Hit percentage based on the JCC orientation for the three profiles and both astigmatism magnitudes, using a dot pattern optotype. a) Profile A: no HOAs; b) Profile B: typical 4th-order spherical aberration and c) Profile C: a combination of high levels of 4th and 6th-order spherical aberration. *Statistically significant differences.
When the cross-cylinder symmetry axis is aligned parallel to the astigmatism patient axis, both profiles A_075 and A_125 exhibit very similar percentages of successful outcomes. In contrast, profiles B_075 and C_075 show higher hit percentages compared to profiles B_125 and C_125, however, the confidence intervals suggest insufficient evidence to establish statistically significant differences.
For other positions (2.5°, 5°, 7.5°, 10°, and 15°), profile A_125, characterized by only low-order aberrations, demonstrates superior performance compared to profile A_075, exhibiting a higher hits percentage, with statistically significant differences noted for the 5° and 7.5° JCC axis positions. Conversely, in profiles B and C, a lower magnitude of astigmatism yields a higher hits percentage compared to a higher magnitude; yet, there is insufficient evidence to confirm the statistical significance of these differences.
Influence of optotypeFig. 6 illustrates the hits percentage based on the type of optotype for both magnitudes of astigmatism across each aberrometric profile. Subfigures 6a), 6b) and 6c) shows the results for profiles A, B and C, respectively, with an astigmatism magnitude of −0.75 D. Subfigures 6d), 6e) and 6f) display the results for the same profiles with an astigmatism magnitude of −1.25 D.
Hit percentage based on the JCC axis position for both optotypes and astigmatism magnitudes. Panels (a–c) show results for −0.75 D of LOAst, and (d–f) for −1.25 D of LOAst. 6.a and d Profiles without HOAs (A); 6.b and e Profiles with typical 4th-order spherical aberration (B); 6.c and f Profiles with a combination of high levels of 4th and 6th-order spherical aberration (C). *Statistically significant differences.
The data indicate that for the profile without HOAs (profile A), there are statistically significant differences between dot and letter optotypes (from 5° to 10°), with dot pattern achieving a higher success rate for both magnitudes of astigmatism. In profiles with HOAs (B_075, B_125, C_075 and C_125), the mean percentage of hits tends to be somewhat higher with the letter optotype, however, differences had non-significant meaning.
For profile A, the hits percentage is 100 % at 20° and remains constant at 30°. In contrast, for profiles with HOAs (B and C), there is a decrease in the percentage of successful outcomes between 20° and 30°. At 20° off-axis, profiles with HOAs do not achieve a 100 % success rate with any of the optotype and astigmatism combinations. Furthermore, at 30° off-axis, the percentage of successful outcomes slightly decreases compared to 20°.
Finally, patients were asked to subjectively assess which optotypes (letters or dots) made it easier for them to discern a preference between Image 1 and Image 2. The results revealed that, out of 40 participants, 29 (72.5 %) found it easier to select the letter pattern, while 11 (27.5 %) preferred the dot pattern.
DiscussionThe present study aimed to investigate the accuracy of patients' responses, assessed by the hit percentage, during the JCCT, considering various factors that could influence the results. To our knowledge, it is the first study able to estimate the influence spherical HOA on the JCCT.
There are few studies24,25 aimed at studing the limitation of conventional refractive procedures in eyes with extreme spherical aberration as multifocal contact or intraocular lenses are. In particular, Perches et al.15 simulated retinal images of a dot pattern that would be produced during a JCCT in a subject wearing no contact lens and with mutifocal contact lenses. They found that in the presence of aberrations, both image pairs are irregularly blurred making image quality comparisons cumbersome. From Fig. 4, it can be noted that aberrometric profile significantly influences the accuracy of patient responses, increasing the difficulty in selecting the axis orientation for profiles with HOAs. This difference becomes more evident at 2.5°. Furthermore, as the JCC rotation deviates from the corrector cylinder axis (from 2.5° to 15°), the curve's slope is lower for profiles B and C. This trend indicates a slower increase in correct responses compared to profile A.
Another noteworthy observation in relation to HOAs influence (refer to Figs. 4-6) is the reduction in correct responses when the JCC axis is at 20° and 30° for both optotypes. In contrast, profile A achieves a 100 % success rate. To explain this decline, Fig. 7 presents a pair of retinal images for profile B_075 with a line of letters, specifically at 30° off-axis. It is evident that a double image, halo or blurring associated with the presence of HOAs difficuls the choice between pairs of images. For this situation even though the correct option to find the correct cylinder axis is Image 1 (where the double image is closer), it is plausible that some observers might prefer Image 2 because the letters appear more readable since they are double distinct images. This kind of situation does not happen when there is no spherical HOA.
Analyzing the results according to the magnitude of astigmatism for each profile, it is observed that in profile A, there is a more pronounced decrease in correct responses for an astigmatism of −0.75 D (compared to −1.25 D). In contrast the opposite trend is observed for the spherical aberration profiles, where −0.75 D astigmatism corresponds to bigger accuracy, even though these differences are not statistically significant. A possible explanation for this phenomenon is that the discernibility of images presented during rotation in a profile containing only low-order aberrations (profile A) improves with increased astigmatism due to the greater distinctions between them. However, with HOAs, this effect appears to diminish, potentially because the pronounced double image caused by higher levels of astigmatism may overlap, making selection more challenging. In any case, as suggested by the graphs, it manifests that the correlation between the magnitude of astigmatism and accuracy appears to be somewhat linked to the presence of aberrations.
Our results (see Fig. 6) also indicate that the patient's responses accuracy is slightly different depending on the aberrometric profile for different optotypes. Our results agree with Pascal's work26 the dot pattern is more accurate than the letter optotype. Our work hightlights that this advantage is more evident when no HOAs are present. Interestingly, this result contrasts with the observers' preference regarding which optotype they found the easiest for performing the visual quality discrimination task: the row of letters. For this situation it seems that ease does not go hand in hand with response accuracy.
In the current study, 4th-order spherical aberration coefficients (Z₄⁰) of +0.20 μm and +0.39 μm, as well as a 6th-order spherical aberration (Z₆⁰) of +0.08 μm, were respectively used. These values are lower but comparable to those corresponding with 4th-order spherical aberration of +0.57 μm for patients with center-distance multifocal contact lenses,27 or with +0.55 μm for post-LASIK myopic cases.28 Following the trend indicated in this work, lower precision in patient response when determining the axis of the corrective cylinder must be expected for higher HOAs.
The observed trend in this study, where the hit percentage increases as we move away from the patient's axis, supports the notion that, ideally, when initiating the JCCT, the positioning should be away from the subject's astigmatism axis. Our results indicate that when a subject has HOAs (for instance due to a multifocal compensation), the optimal positioning of the JCC axis should be further away from the subject's axis compared to a subject without HOAs. Specifically, to achieve 90 % accuracy, the JCCT should be initiated by deviating >7.5° from the subject's astigmatism axis if no HOAs are present, and >15° if HOAs are present.
Nevertheless, this study has limitations that must be mentioned. The main limitation is that the aberrometric profiles A, B and C are synthetic, and only positive spherical aberration has been considered. Additionally, accommodative and pupil dynamics and chromatic aberration were not included in the image simulation performed in this study. In a future study, a wider range of regular astigmatism and HOA profiles must be considered, this includes negative spherical aberration (typical from LASIK hyperopia patients28 or those using center-near multifocal lenses27) or coma (typical from corneal ectasias29 and IOL dislocations30). Furthermore, although it is a challenging task, it will also be interesting to validate how the obtained results can be extrapolated to a real environment.
Conclusions- •
For optimal results, the JCCT should be initiated by deviating from the ocular astigmatism axis by >7.5° when no HOAs are present, and by >15° when HOAs are present.
- •
The relationship between the astigmatism magnitude and accuracy appears to be weakly linked to the level of HOA aberrations.
- •
Despite the difficulties that the dot pattern causes in comparison with a row of letters, a dot pattern must be chosen to achieve the highest rate of correct responses for aberrometric profiles that are free of HOAs.
- •
Clinicians should consider both aberrometric profiles and optotype selection to enhance the efficacy of the Jackson Cross Cylinder Technique to find the axis of the ocular astigmatism.
This research was supported by Ministerio de Ciencia, Innovación y Universidades (Grant PID2020–114311RA-I00) and Gobierno de Aragón (Grant E44–23R). D. G. Y. was supported by Gobierno de Aragón.