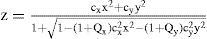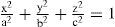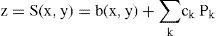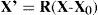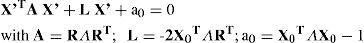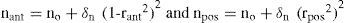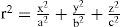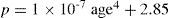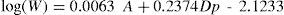Cornea, lens and eye models are analyzed and compared to experimental findings to assess properties and eventually unveil optical design principles involved in the structure and function of the optical system of the eye. Models and data often show good match but also some paradoxes. The optical design seems to correspond to a wide angle lens. Compared to conventional optical systems, the eye presents a poor optical quality on axis, but a relatively good quality off-axis, thus yielding higher homogeneity for a wide visual field. This seems the result of an intriguing combination of the symmetry design principle with a total lack of rotational symmetry, decentrations and misalignments of the optical surfaces.
En este trabajo, los modelos de córnea, de cristalino y de ojo se analizan y se comparan con los datos experimentales para evaluar las propiedades y, eventualmente, para desvelar los principios del diseño óptico que afectan a la estructura y al funcionamiento del sistema óptico del ojo humano. A menudo encontramos una coincidencia razonable entre los modelos y los datos experimentales, pero también se ponen de manifiesto algunas paradojas. El diseño óptico parece corresponderse con el de un gran angular. En comparación con los sistemas ópticos convencionales, el ojo tiene una mala calidad óptica en eje pero, por el contrario, presenta una calidad relativamente buena fuera de eje, proporcionando así una gran homogeneidad a una amplia extensión del campo visual. Este hecho parece ser el resultado de una curiosa combinación del principio de diseño simétrico con una total ausencia de simetría de rotación, con descentramientos y con una deficiente alineación de las superficies ópticas.
Our understanding of the optical system of the eye is evolving quite rapidly due to the combined effort of new experimental methodologies and advanced modeling. Optical design plays a central role here since this branch of science and technology deals with finding the best combinations of optical elements (lenses, etc.) to obtain a desired function, with optimal performance. Optical testing is also necessary for the verification and validation of designs. The study of the optical system of the eye has similarities, but also remarkable differences with optical design and testing. The optical design of the eye is already given by nature (optimization through evolution), so its study can be seen as an inverse engineering problem: to unravel such design. Inverse problems are difficult in general and must be solved by successive approaches. Each approach consists of (1) some starting hypothesis based on previous knowledge; (2) a set of experimental data; and (3) a model relating those data and the hypothesis. The testing stage (4) compares model predictions to experimentally assessed optical performance. In the general case some agreement, and also important discrepancies, are obtained. The analysis of these discrepancies leads to the formulation of new hypotheses; therefore, a new approach should be undertaken. One interesting example is the intra-capsular mechanism of accommodation hypothesized by Gullstrand1 to explain discrepancies between geometry and power of his accommodated eye model (this example will be analyzed below.)
It is crucial to realize that models and underlying hypotheses affect not only the way we understand the eye, but everything involved in the study of the eye; from measurement instruments, to data analysis and interpretation of results. Thus models make our ideas evolve and models progress with new experimental knowledge. This also affects clinical practice.
To understand the optical design of the eye we need models of each component (cornea, lens) and from that we can construct a model of the complete optical system. An initial overview of the literature shows a great variety of models, mainly attending to the following features:
- -
Reduced (single refractive surface)2,3 versus anatomical (cornea and lens),4,5
- -
Monochromatic6 versus polychromatic7,8 (considering refractive index dispersion),
- -
Paraxial4,6 versus finite optical performance7,9,10 (optical and image quality),
- -
- -
- -
- -
- -
Other relevant aspects, such as intraocular scattering, have been incorporated only in a few models.24 However, the GRIN lens distribution or structure has attracted the interest of numerous authors. In fact, most of the crystalline's models consider the GRIN structure within the lens.5,11,13,16-18,20,25-29
Such variety of models reflects the fact that all models are incomplete, since the real human eye contains both cornea and lens (anatomical), works with polychromatic light, it is known to have a limited optical performance (aberrations), it has a very wide visual field, it uses accommodation to focus near objects and it evolves throughout life span. Above all, any model must account for short-term (accommodation) and long-term (ageing) changes.
Finally, generic (average) models are of greatest importance to understand the optical design of the eye, but they do not correspond to real individual eyes. This is similar to statues in the classic period in ancient Greece. Each represented part of the body or feature was canonic (obtained by some sort of average) and as a result, these statues display a superb magnificence. Therefore, these correspond to ideal human body designs rather than to real human beings. Thus, while canonic or generic eye models are important to understand the optical design of the human eye, personalized eyes are essential to develop clinical applications, such as custom treatments.
The goal of this review is to extract underlying optical design principles in the human eye from the analysis of models and data. The two main optical elements –cornea and lens– are analyzed in separate sections and then the complete optical system is considered along with a final section of concluding remarks.
Optics of the Human CorneaModelsThe cornea is a meniscus lens. Its anterior surface is the interface between the air and the eye, and is by far the surface wirh the highest refractive power in the human eye, about 48 D (diopters).6 Historically, modeling of the eye was limited to first-order Gaussian optics, meaning that all optical surfaces were considered as spheres. The corneal surface was thus described by a single variable, its radius of curvature R. However, spherical surfaces were found to predict much greater spherical aberration and oblique astigmatism than that actually measured.11,30 This discrepancy was avoided by simply introducing more realistic conic surface models.9 The conic model still assumed rotational symmetry, yet normal corneas often show astigmatism, and usually there is a greater radius of curvature at the horizontal than at the vertical meridian. This has been often referred to as toricity.31 Toric and conic models can be combined using more realistic biconic surfaces.32 The sagitta z of a biconic surface is given by the expression:
This surface is characterized by 4 parameters: two orthogonal curvatures, cx=1/Rx and cy=1/Ry, and their corresponding conic constants Qx and Qy. This model is fairly complete, contemplating most of the basic optical properties of the cornea. Additionally, it is relatively simple to rotate the coordinate axes X,Y around the optical axis Z, to align them to the axis of astigmatism (the rotation angle would be the fifth parameter in the surface model). It is straightforward to show that the biconic model includes all the previous ones: The spherical model with a single parameter, R, corresponds to the particular case when Qx=Qy=0 and Rx=Ry=R. The revolution conic model is the case when parameters Qx=Qy=Q and Rx=Ry=R. The toric surface has two curvature radii along the two orthogonal meridians. A biconic with Rx, Ry, and Qx=Qy=0 is a good aproximation to the toric surface. For the general biconic there are no constraints on any of the four parameters. The only drawback of biconics is that they are fourth-order surfaces. A second-order alternative is the 3-axes non-revolution ellipsoid, in canonical form:
where a, b and c are the semiaxes. This ellipsoid can be expressed also as a biconic (Eq. 1), through the following relations: Rx=a2/c; Ry=b2/c; Qxa2/c2-1; and Qy=b2/c2-1, but the ellipsoid is less general since it only has 3 independent parameters. The main advantage is that this is a simpler second-order surface. Eqs. 1 or 2 represent most of the basic surface models of the cornea that are currently employed.In practice, the topographies of real corneas do not match exactly any of these ideal models, but, rather, they exhibit different irregularities and departures from that basic geometry. The difference, or residual, between the actual topography and the ideal basis surface model (Eqs. 1 or 2) is often adjusted to some sort of orthogonal polynomial expansion, or interpolating functions such as splines.33 The Zernike polynomial expansion is the most commonly used method.34,35 Then the corneal surface is described by
where the corneal surface S is the sum of a regular basis surface b(x,y) (biconic, ellipsoid, etc.), and an irregular component, modeled as a Zernike polynomial expansion, where each polynomial Pk represents a surface deformation mode and ck is its magnitude (coefficient). These models are much more general and realistic and, in fact, they are able to fit real corneal topographies. The main drawback of polynomial expansions (splines, etc.) is that they can potentially fit any shape, but their coefficients do not have invariance properties of physical magnitudes and are difficult to interpret. As an example, the curvature radius or the conic constant are invariant under rotations or translations of the surface, whereas Zernike coefficients may largely change. Closely related to this problem is another essential feature of the cornea: human corneas use to be misaligned, tilted and slanted with respect to the measuring device. The (intrinsic) optical axis of the cornea is different from the keratometric axis used by the topographer.36 The cornea has three major reference points, related to three important axes: the vertex normal (VN) or corneal intercept of the keratometric axis; the corneal sighting center (CSC), intercept of the line of sight; and the corneal apex (CA), intercept of the optical axis, and point of maximum curvature (for prolate corneas). Mandell et al.37 found an average displacement of about 0.6mm from the apex to the vertex normal, as well as differences in the refractive power among these three points, the apex, VN and CSC.One way to take into account this essential fact is to realize that the topographer views a translated and rotated version of the corneal surface. In mathematical terms this is a lineal affine transform, so that the intrinsic coordinates of the surface (x, y, z) are transformed into the system of coordinates of the topographer (x’, y’, z’). In vector-matrix formulation:
where R is a 3×3 rotation matrix and X0 is a displacement vector. Then, from the point of view of the instrument, the coordinates in Eqs. 1, 2 or 3 are transformed by Eq. 4, so that the expressions change accordingly. For instance, we can rewrite in matrix form Eq. 2, which becomes XT ΛX=1, where Λis a diagonal matrix, whose diagonal elements are 1/a2, 1/b2, 1/c2 respectively. If we now apply the affine transform (Eq. 4) to Eq. 2, it becomes:A is a symmetric matrix with 6 different elements, L is a vector with 3 components and a0 is a scalar. Eq. 2 is the canonical form, while Eq. 5 is the expression of a general ellipsoid. Linear algebra permits us to change the coordinate system, and to go from the general to the canonical representation.38 In this way we can obtain the position and orientation of the intrinsic axes of the cornea (optical axis, Z; astigmatism axis Y, and the remaining orthogonal axis X). It is important to note that the affine transform of Eq. 4 reflects the change of the intrinsic Cartesian coordinate system of the cornea (aligned with its principal axes of symmetry) to the coordinate system of the measuring instrument. This transform is independent of the particular type of surface assumed, but is essential to include it to have realistic physical models of corneal topography.
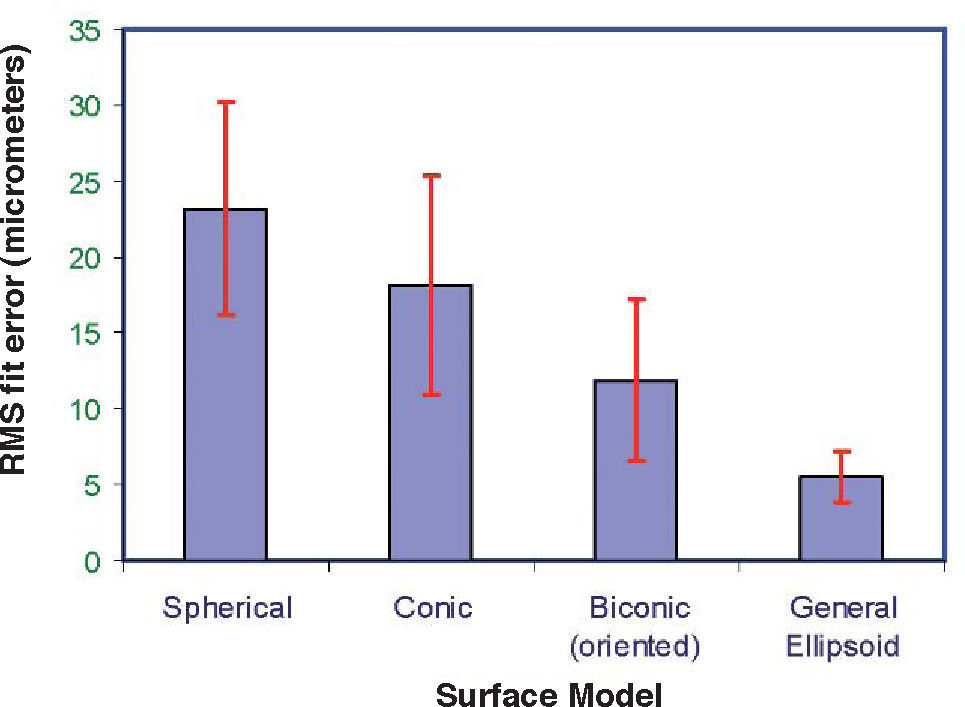
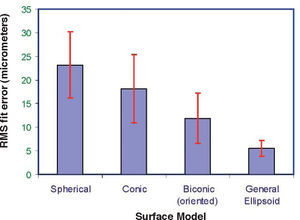
The relative importance of the different parameters and the need for realistic models can be assessed by comparing the goodness of fit obtained with real topographies. In Ref. 38, the models described above were applied to fit 123 corneal topographies. The averages of the resulting RMS fit errors are shown in figure 1 for different models. It is patent that the fit error decreases as the model becomes more realistic. A simpler ellipsoid model, but in general form (free position and orientation) provides significantly better fit to the data than the more complex (but canonical form) biconic model, even though the orientation of the latter was optimized to match the axis of astigmatism. This confirms that the intrinsic corneal coordinates are different from those of the instrument, and hence the importance of considering the affine transform of Eq. 4. As an additional result, the amount of residual (deformation) that one has to fit to a Zernike polynomial expansion is much lower.
DataThe above models are general enough to be applied to any refractive surface of the eye, including both surfaces of the cornea.
Anterior SurfaceMost studies of corneal shape are focused on the anterior surface due to two main reasons. On the one hand, the refractive power of the back surface is much lower than that of the anterior surface (about -6 D versus 48 D); and on the other hand, measuring the back surface is more difficult and the resulting topographies are much less reliable. The most relevant studies of the corneal shape until year 2000 have been reviewed in Ref. 31. Most of these studies39,40,41 assume conic or (implicit or explicit) biconic models, and provide consistent results for the mean radius R close to 7.83mm31 and mean conic constants Q usually between −0.18 and −0.3 (indicating, a slightly prolate, shape) for the population-average, corneal astigmatism (due to corneal toricity) is slightly below −0.5 D with a leptokurtic (skewed) distribution.42 Experimental results in these studies could be potentially biased because (1) they rely on too simple unrealistic assumptions (they use models in canonical form) and (2) the measurements are limited to a central zone of the cornea. (The area covered varies across studies).
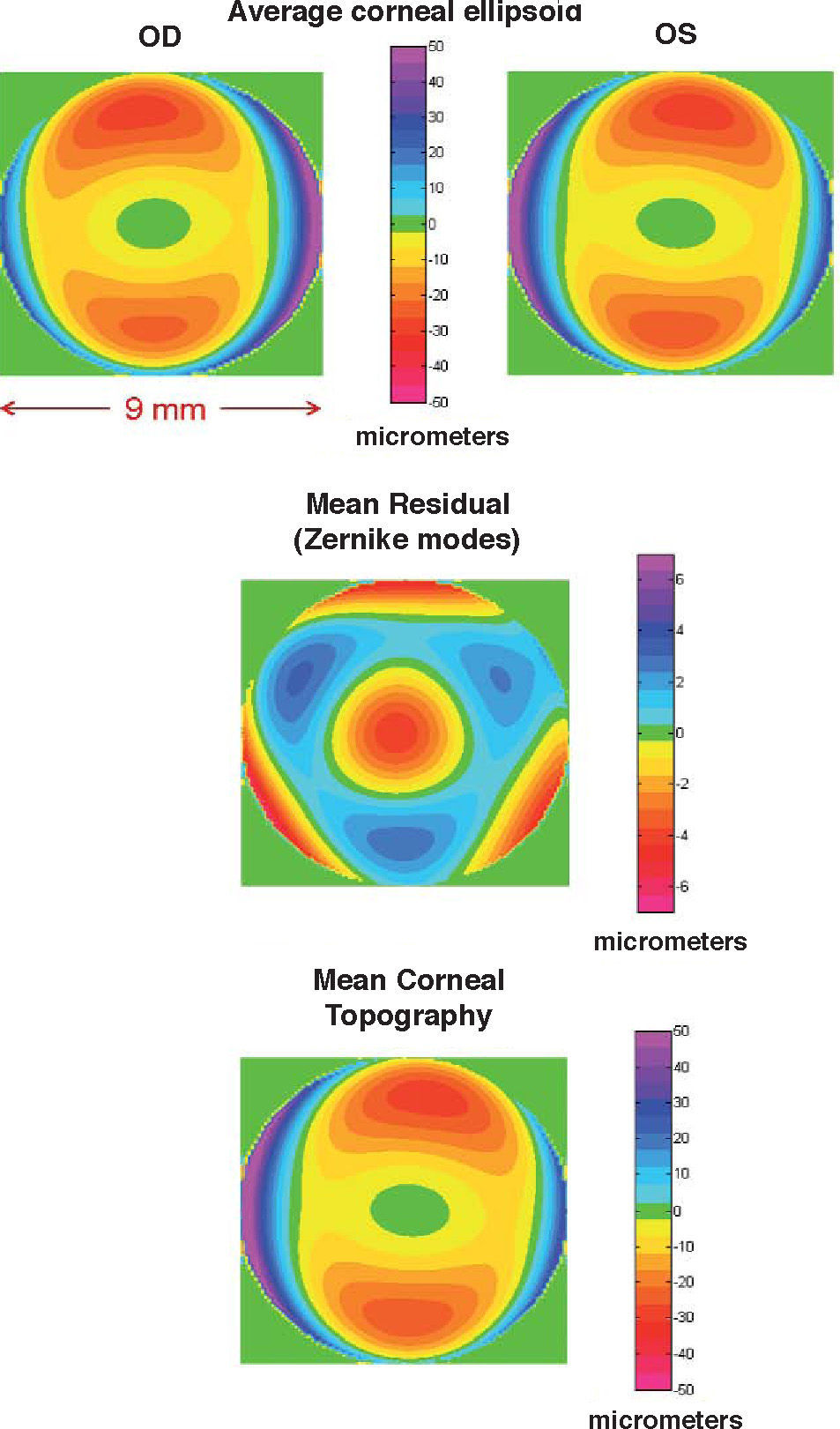
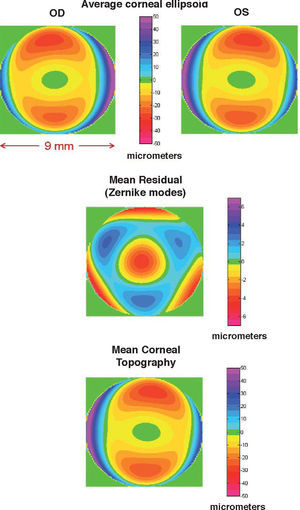
When one attempts a more realistic model (general ellipsoid + Zernike polynomial expansion of the residual) to all the corneal surface covered by the topographer (diameter equal or greater than 9mm) the cornea appears as an off-axis melon-shaped ellipsoid with some additional deformations,38 as shown in figure 2. The upper panels compare the averaged corneal ellipsoids (112 eyes), showing a high mirror symmetry between left and right eyes. The ellipsoids are clearly off-axis with their axes rotated by average angles 2.35°±2.3° (nasal) and 0.85°±2.74° (up). The corneal, apex is also displaced from the vertex, VN (average 0.3±0.3mm and 0.1±0.3mm in the horizontal and vertical directions respectively). Apical curvature radii Rx=7.63±0.29mm and Ry=7.4±0.28mm are significantly lower than the radii found in previous studies due to two reasons. On the one hand, corneal ellipsoids are found to be significantly more prolate (Qx=−0.46±0.14, Qy=−0.48±0.14). This means that the curvature at the apex should be higher (lower radius), to keep the same surface average curvature. On the other hand, the apex is the point of maximum curvature, whereas previous models, using ellipsoids in canonical form, assume that the maximum curvature is at the VN, which would tend to yield lower curvatures (higher radii). In addition, toricity is found to be higher, and hence corneal astigmatism is higher too. The average topography found for these 112 corneas is shown in the lower panel, after adding the residual (central panel). In that particular study only 3 Zernike deformation modes were significally different from Zero (4th- and 6th-order spherical and trefoil).
Posterior SurfaceThe posterior surface of the cornea has been extensively studied, with especial emphasis on its relative contribution to the corneal optical properties.41,43,44 The back surface of the cornea is difficult to measure, but new instruments such as corrected Scheimpflug photography45 or promising methods such as anterior segment OCT imaging might help to make highly accurate in vivo measurements. Classic values for the posterior curvature radius are lower than the anterior surface, about 6.5mm, whereas the conic constant seems to be more negative, about −0.6641 (more prolate ellipsoid). The mean apical corneal thickness is around 0.54-0.55mm.
Tear LayerThe tear layer is essential to ensure a good optical quality of the corneal surface. The corneal epithelium is its outer layer and has a rough, low quality surface. The tear covering fills out epithelial roughness, and small irregularities or defects (scratches, etc.) The role of the tear film in the optical quality of the human eye has been extensively studied (see Ref. 46 for a review). While there is evidence and a general consensus on its role in avoiding scattering from the corneal surface, there is some controversy regarding its role on ocular aberrations. Most studies suggest some influence on HOA (higher order aberrations), but different aberrometric and interferometric measurements seem to provide substantially different amounts to the relative contribution.
Similarly to the anterior surface, the corneal endothelium also displays a rough surface. Here the aqueous humor (AH), having basically the same refractive index as the tear layer, plays a similar role minimizing scattering. Nevertheless, the situation is somewhat different because the AH is not a thin coating but fills the anterior chamber.
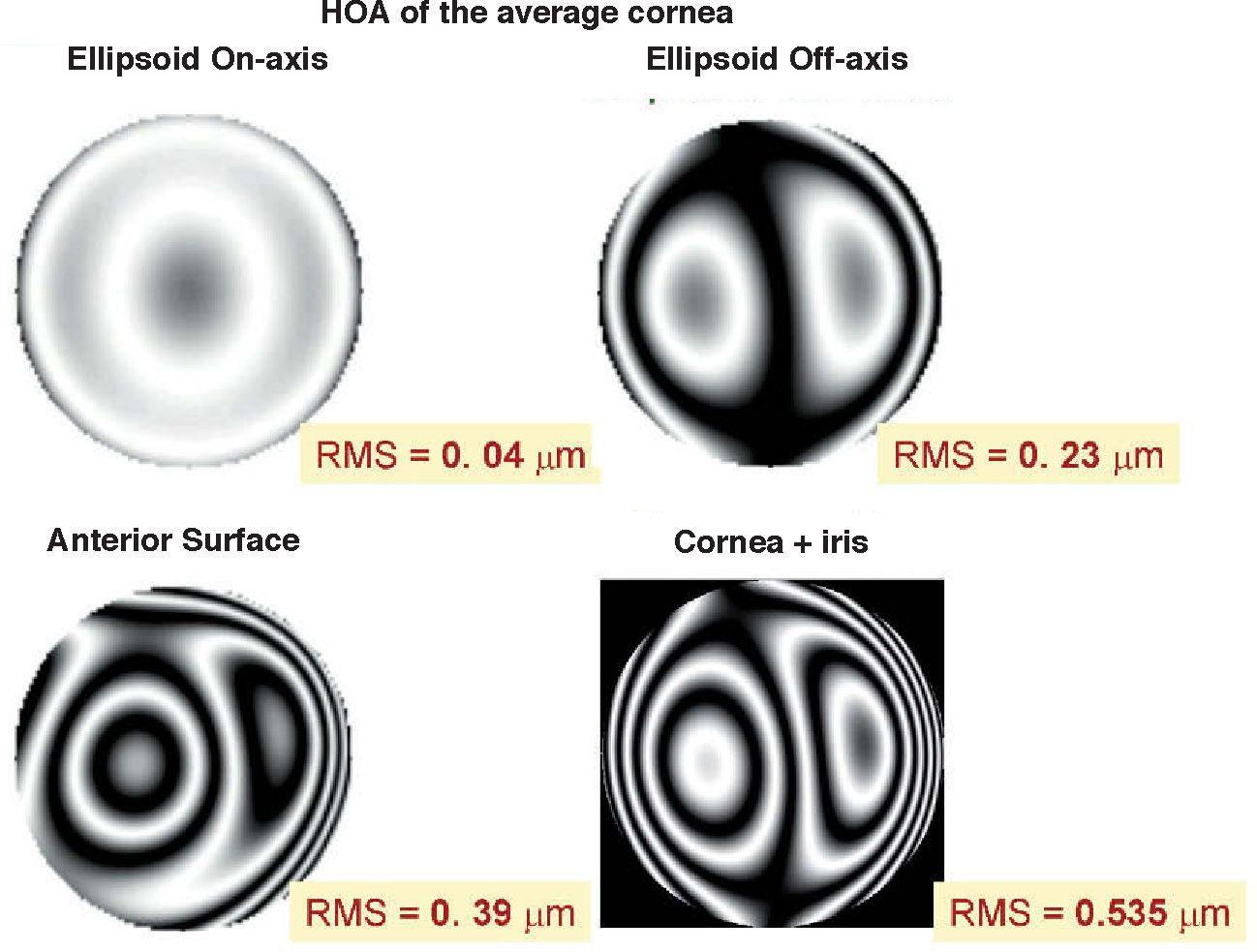
Optical PerformanceThe optics of the cornea has been extensively studied. Assuming a refractive index of 1.376, the power of cornea of the Gullstrand eye model4 is slightly above 43 D, and the average astigmatism around 0.45 – 0.48 D.42 Higher order aberrations (HOA) have been also studied, usually through ray tracing computations from corneal topography data.47,48 The cornea shows high values of HOA, higher than total values measured for the optical system of the eye. This partial compensation by internal optics (mainly the lens) was confirmed in many studies49,50 and predicted by most eye models.7Figure 3 shows the wave aberration (HOA only) for the average topography of figure 2.
The underlying optical design of the cornea is surprising because, as we can observe, the average corneal ellipsoid is almost corrected for spherical aberration (upper left panel), due to the fact that its conic constant is close to the optimal value (−0.528).31 However, since the ellipsoid is off-axis, there is a strong contribution of coma (upper right panel). If we add the residual (Zernike deformation modes) to reconstruct the topography, then the RMS wavefront error is almost double, with an important increase of spherical aberration, coma and trefoil. When we include the back surface, and a decentered pupil (about 0.5mm nasally)51 we get a further increase of HOA. In addition to these HOA, we have a strong contribution of astigmatism (about 0.5 D). Of course, individual corneas may have quite different performance, but since average tends to smooth or even cancel random deformations, the performance of the averaging cornea is expected to be more representative of good, rather than bad, corneas. In essence, the cornea shows a quite modest optical performance, and introduces significant amounts of aberrations into the optical system of the eye, mainly astigmatism and coma, followed by spherical aberration, trefoil, etc. The main sources of aberrations seem to be: the angle between the visual axis and the optical axis, surface irregularities (deformation modes) and pupil decentration.
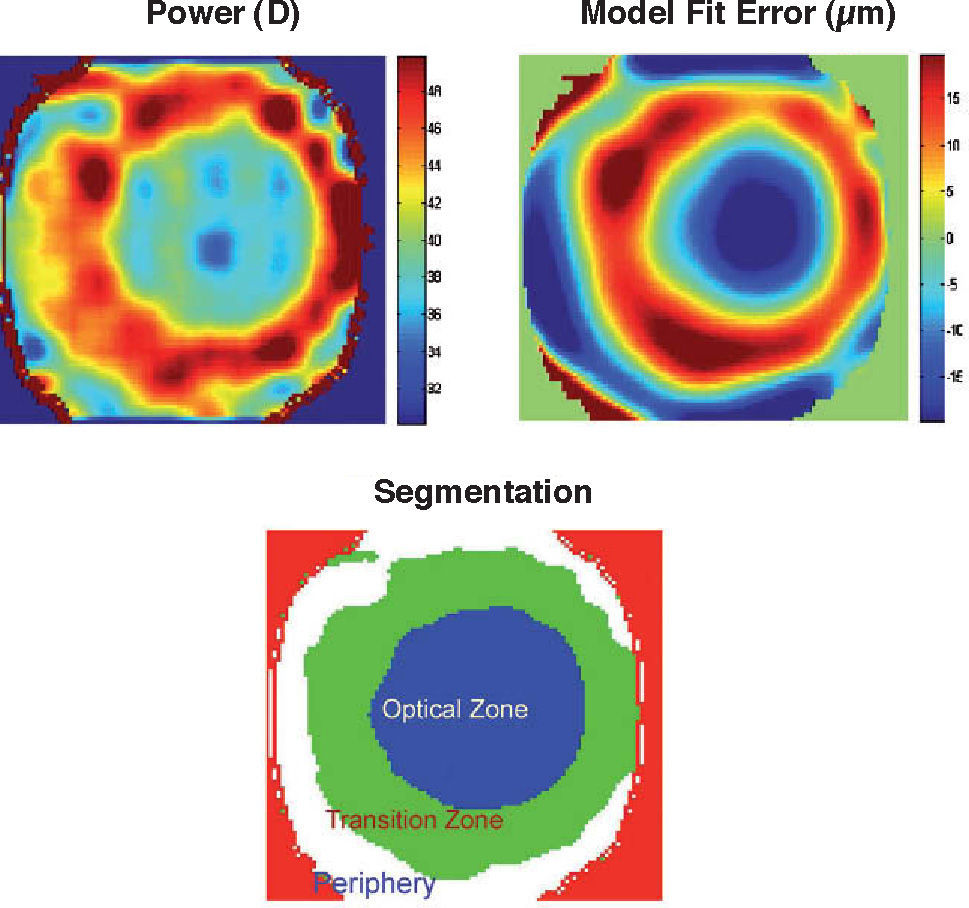
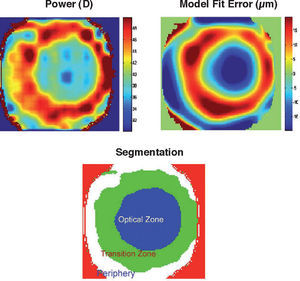
Postsurgical & Keratoconus CorneasThe above models and data correspond to normal healthy corneas. Some pathologies cause corneal deformations (corneal warping, keratoconus, etc.). In addition, nowadays there are many hundreds of thousands of post-surgical eyes (after cataract or refractive surgery) and this number is increasing rapidly. Surgery is known to modify the cornea, usually increasing HOA and scattering. Several authors have proposed methods (expert systems, etc.) for automatic screening of keratoconus52 or for the classification of corneas.53 It has been pointed out54 that standard model fitting fails to represent significant corneal aberrations for these eyes. For abnormal corneas, multizone models55 seem more appropriate. The idea is to split the corneal surface into different zones and then apply a standard model to analyze each zone independently. The total surface is obtained as the union of zones. For instance, the area of a keratoconus can be one zone, and the remaining cornea the second zone. Figure 4 shows an example of a post-LASIK cornea with 3 zones, optical zone, transition zone and the untouched periphery. The two upper panels represent the refractive power in dioptres (Gauss curvature, left) and the fit error to the standard model in micrometers (general ellipsoid, right). Both figures suggest the presence of three zones. After applying an automatic classification method, we obtain the segmentation into the three zones, with quite different optical properties. As a result, this post-surgical cornea is a sort of bifocal meniscus with less than 40 D, except for a ring with more than +6 D of addition. The transition ring seems to invade some area of the nominal (planned) optical zone. This will have an impact on visual quality for large pupils (night vision).
Optics of the Crystalline LensWhile corneal topographers have permitted to collect huge amounts of data, thus demanding the development of realistic models, the human lens represents the opposite case. Most data and models come from in vitro studies, and only a reduced number of techniques such as Scheimplug imaging56-58 permit to obtain one-dimensional (1D) profiles of the lens surfaces. Data from in vitro studies are scarce and limited to 1D profiles.59,60 In principle, mathematical models used for the cornea are general enough to be applicable to the lens surfaces, but as far as I know, lens topographies (2D maps) have not been published yet. In all these studies the lens surfaces are assumed to be conics with revolution symmetry. More realistic models of the lens shape have not been used mainly because of the lack of experimental data. Experimental studies face important limitations. On the one hand, the lens changes with accommodation and continuously grows with age. Therefore, in addition to intersubject variability, the lens presents huge variations with time, both fast (or short-term, accommodation) and slow (or long-term, aging). In addition to these sources of variability, the in vivo study of the lens is difficult because the lens has to be imaged through the cornea which causes blur, perspective and optical distorsions.45 A further difficulty is that shapes in vivo and in vitro cannot be compared since the living lens is under the stress of the ciliary muscle. Even though artificial stretchers have been developed61 to simulate the action of ciliary forces, it is difficult to make direct comparisons. Most authors assume that the shape of the in vitro lens corresponds to a fully accommodated state. Dubbelman and co-workers have reported an empirical model of the changes of the lens surfaces with age and accommodation,58 shown in table 1.
Geometry of the lens surfaces as a function of age (A, years) and accommodation (D, diopters). R and Q are curvature radii and conic constants, respectively, (see Equation 1) of the anterior (a) and posterior (p) surfaces and t is axial thickness
| Ra=1/[1/(12.7-0.058A)+0.0077D] mm | Qa=−4 −0.5D |
| Rp=−1/[1/(5.9-0.013A)+0.0043D] mm | Qp=−3 |
| t=2.93+0.0236A+D(0.058−0.0005A) mm | |
An additional complexity of the human lens is its gradient index (GRIN) structure. This fact was already studied by Gullstrand.4 It is worth saying that GRIN data on human lenses are even more scarce,62-65 whereas much more modeling work13,16,19,20,27-29,66,67 has been done. There is a general consensus that the refractive index of the lens seems to increase monotonically from the surface to the center and also that the GRIN structure increases the refractive power of the lens. However, different models may show large quantitative differences. Until recently, most models assumed a quadratic (second-order polynomial of z and r2, where r2=x2+y2) distribution of refractive index, which means a linearly distributed gradient. However, more recent experimental data63,65 suggest a nearly homogeneous nucleus, and a GRIN cortex. Such distribution does not fit second-order models, but a 6th-order expression has been proposed.67 The distributions of refractive index for the anterior and posterior parts of the lens are given by:
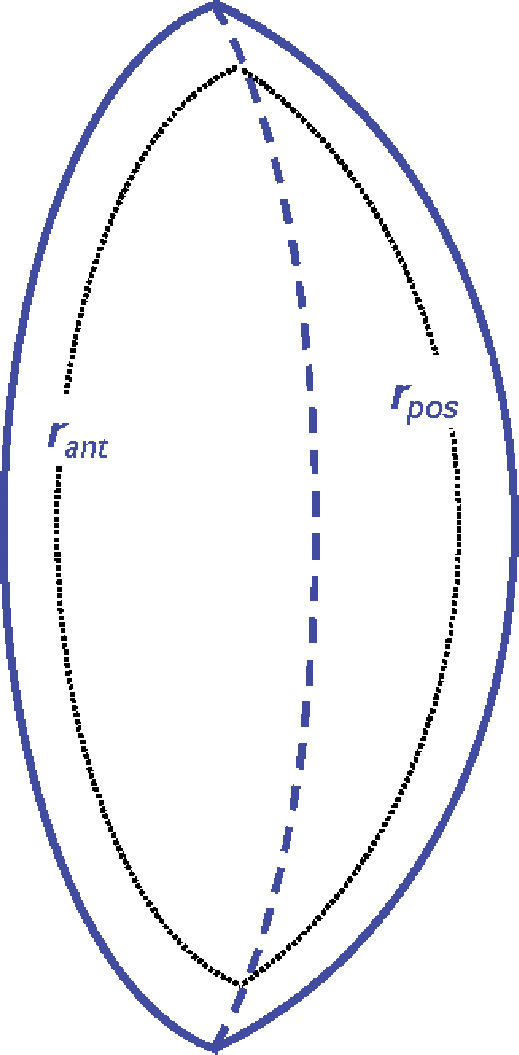
with P=3. Departing from these expressions an adaptive model has been formulated, by considering that the expression r2=constant represents an isoindical conicoid surface. For a conicoid (Eq. 2):In order to guarantee continuity of the left and right hemispheres of each isoindical surface, it was shown that the central interface must be another conicoid surface29 instead of the equatorial plane assumed in previous models (see figure 5).
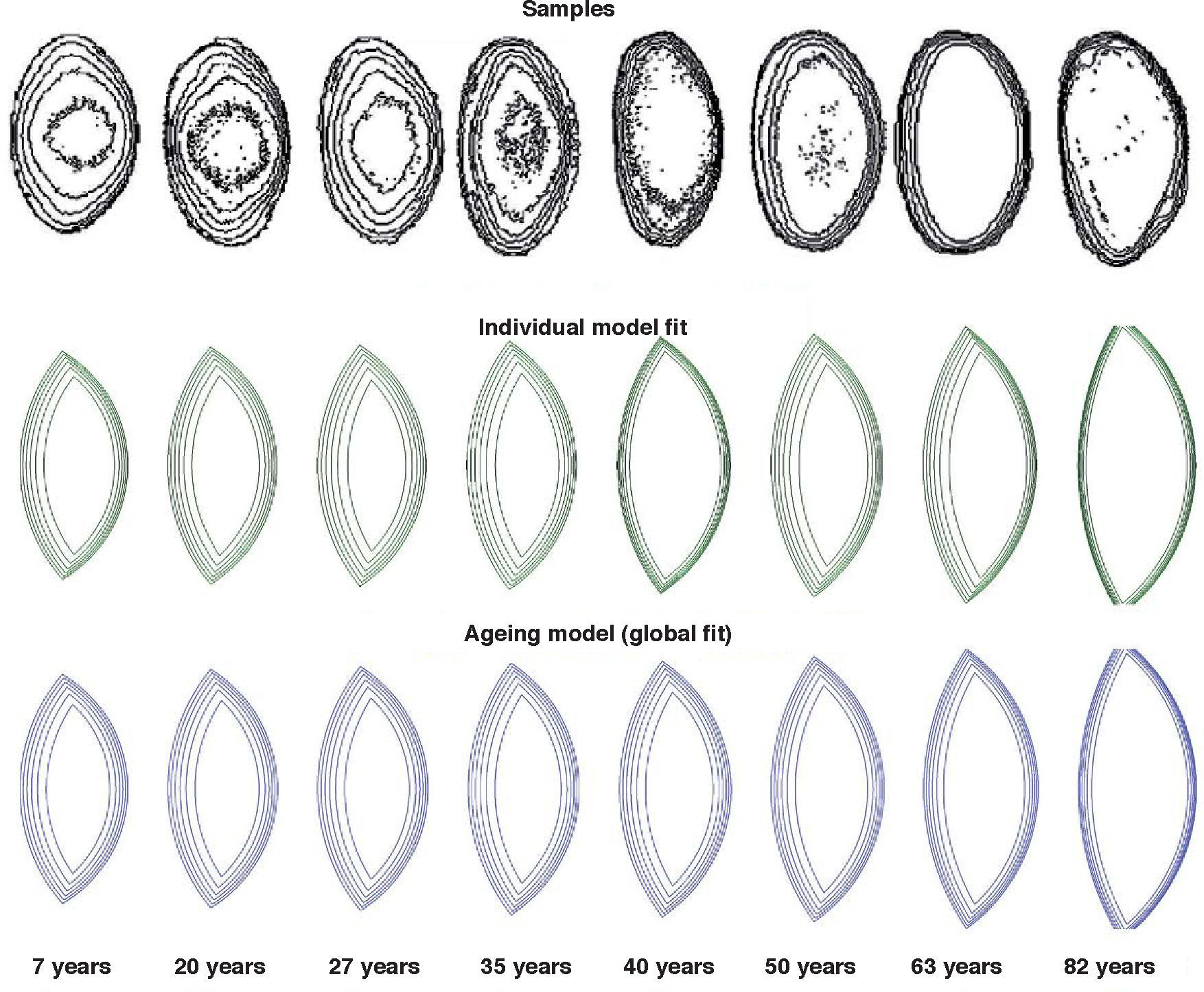
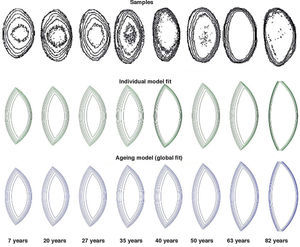
Figure 6 shows the result of applying the adaptive model to fit experimental data. The upper row represents the isoindical surfaces obtained experimentally for a set of ex-vivo lenses of different ages.65 Results of individual fits (sample by sample) are plotted in the middle row. Finally, the lower row shows an aging GRIN lens model obtained from a single global fit on the complete set of samples. The internal structure of the resulting model depends on the shape of the external surface, and has only one age-dependent parameter, the exponent p in Eq. 6:29
Application of an adaptive GRIN lens model to fit a set of experimental data: lens samples of different ages65 (upper row); result of model fit for each sample (middle row); and result of global fit to obtain an ageing GRIN lens mode (lower row).
Thus, p>2.85 and increases with age. For young and middle-aged lenses p is close to 3 so that the refractive index approximately follows a 6th-order distribution. Estimations from recent experimental data65 and models,29 suggest that the optical impact of the GRIN distribution would be significantly lower than that predicted by quadratic models. It is clear that 2nd- and 6th-order refractive index distributions will give different optical properties. Quadratic models with a more homogeneous (linear) gradient predict a much higher contribution of the GRIN structure to the optical power, and general performance, of the lens than more anatomical 6th-order models. In the latter type of models, the nucleus is nearly homogeneous (zero gradient), and the gradient increases towards the edges, where it is maximum. In this case, the actual contribution of the GRIN structure will be much lower. A recent study by Hermans et al.68 suggests that the impact of the GRIN structure is modest. These authors even claim that they can model accommodation with a simple lens model under the assumption that both cortex and nucleus have different but homogeneous refractive indexes. Furthermore, if they consider accommodation lag, then they can totally discard any ICMA (intra-capsular mechanism of accommodation).1 Nevertheless, experimental evidences and models (P>2.85) are compatible with a homogeneous nucleus and a GRIN cortex.
On the other hand, adaptive GRIN lens models predict a strong coupling between conic constants (Q) of the lens surfaces and internal GRIN distribution,69 so that changes in Q (by accommodation or aging) may affect not only the optical quality (spherical aberration, etc.) but also lens power. This is a novel non-intuitive property, which adds complexity to the optical analysis. In classic paraxial optics of homogeneous media (constant refractive index), Q has no effect on focal length, and principal planes. However, in GRIN optical media, where the internal refractive index distribution depends on Q, that property does not hold true. Furthermore, in adaptive GRIN models the internal GRIN distribution is strongly dependent on surface shape (R and Q). In particular, it was estimated that the paraxial lens power would decrease from 22 D to 19.8 D (that is, a 10%) when the conic constants go from 0 (spheres) to negative Qa=−4, Qp=−3 (Qa, Qp are anterior and posterior surfaces) values (hyperboloids). The effect of Q on spherical aberration, SA, is dramatic: SA goes from highly negative values for spheres (Qa=Qp=0), to highly positive values for the hyperbolic (Qa=−4, Qp=−3) surfaces. Therefore, the GRIN structure seems to enhance the role of the conic constants.
OpticsThe human lens contributes with about 1/3 to the total power of the eye at zero diopters of accommodation. The lens power changes strongly with accommodation from about 21-22 D for the unaccommodated state to above 30 D for the fully accommodated lens.3 Most of this strong change is explained by the change in curvature radii of the lens surfaces (see table 1) under the action of the ciliary muscles. Nevertheless, the increase in lens curvature with accommodation is not enough to explain the total increase of power needed to fully accommodate. To explain this discrepancy, Gullstrand1 introduced the ICMA, which is an increase of the equivalent refractive index of the lens. Several authors explained the ICMA by means of the GRIN distribution.70 However, as said above, recent studies68 suggest that the discrepancy disappears if one considers accommodation lag, so that probably the ICMA does not exist. Nevertheless, the optics of accommodation is not totally understood; there are several open questions and an evident lack of experimental data. The number of unknowns is still large to develop realistic models and accurate predictions.
There are three main factors affecting the optical quality of the lens: Scattering, diffraction and aberrations. It is well-known that young healthy lenses are highly transparent, but scattering by the fibrous structure of the lens increases with age. Aging and other factors (pathologies, drugs, infrared or UV light exposure, etc.) may produce the development of cataracts; i.e. a strong increase of scattering and loss of transparency, which cause a severe visual impairment. Cataract surgery is the most common and a highly effective treatment. It consists of replacing the cataractous lens by an artificial intraocular lens (IOL). The optical design of IOLs is a highly active field of research which cannot be extensively addressed in this review. Nevertheless, it is noteworthy to say that there are many hundreds of thousands of eyes with implanted IOLs. Therefore, the study71 and modelling23 of this subset of “modified” eyes is a new important area of research.
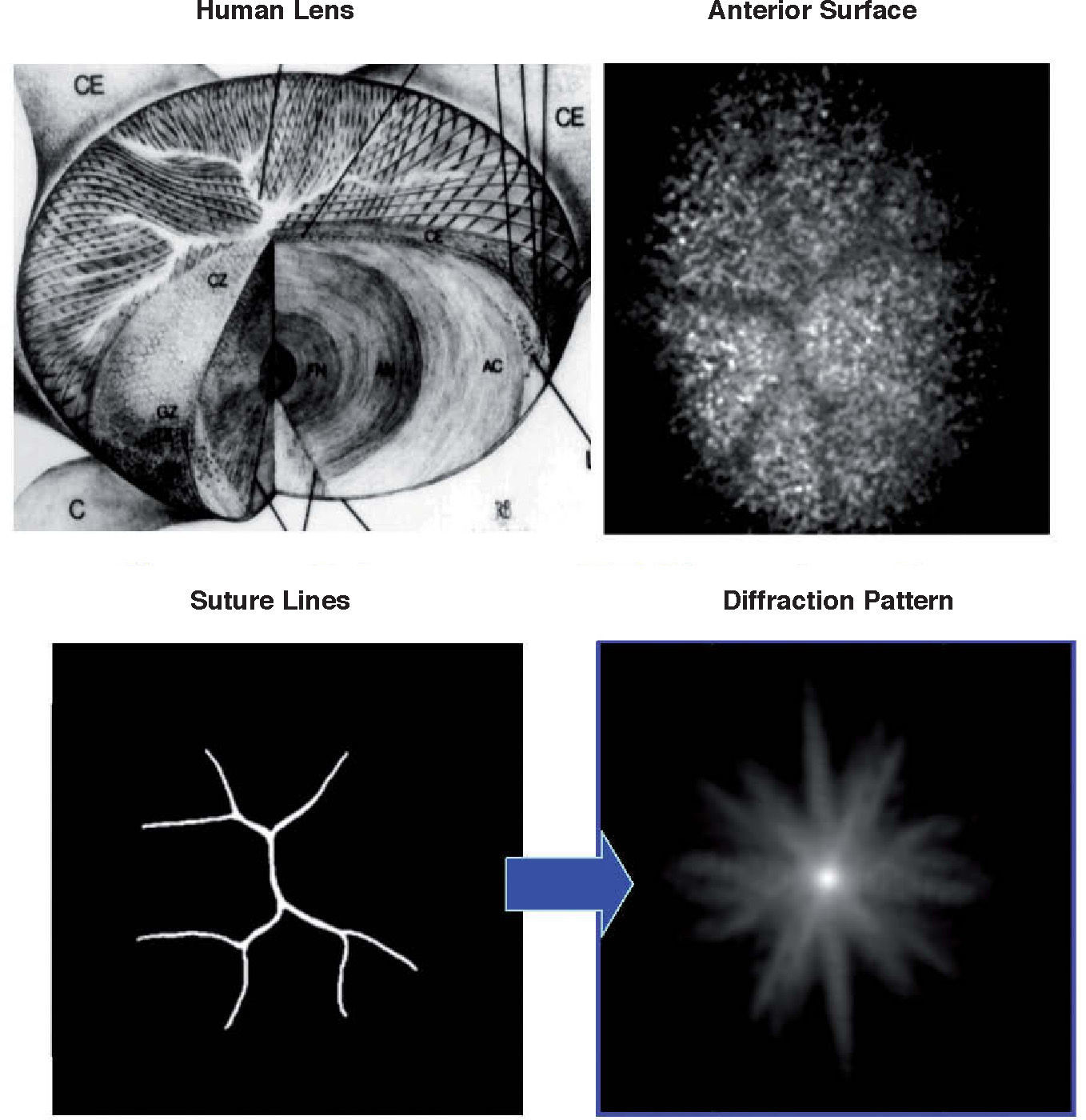
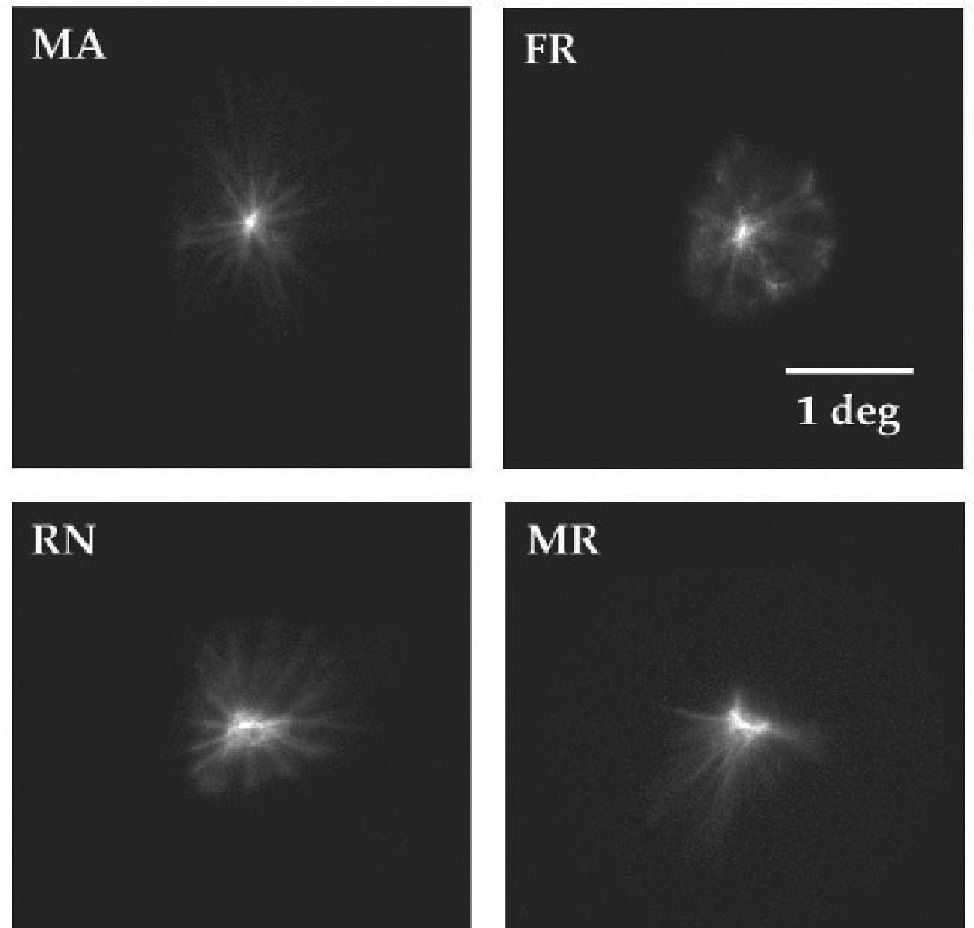
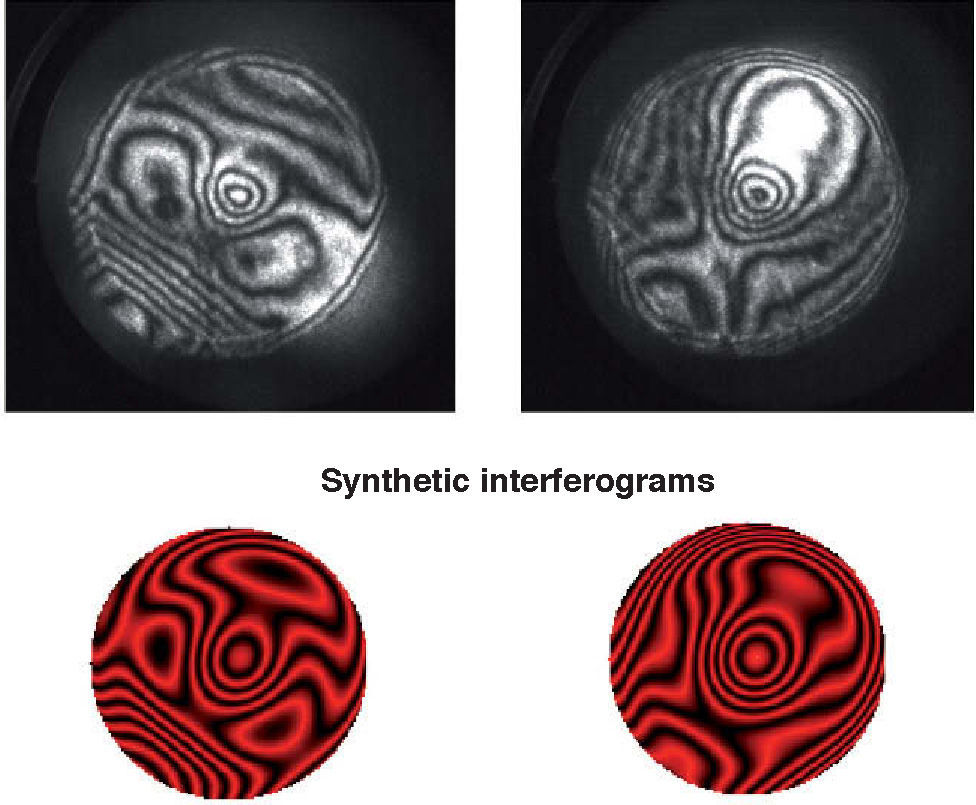
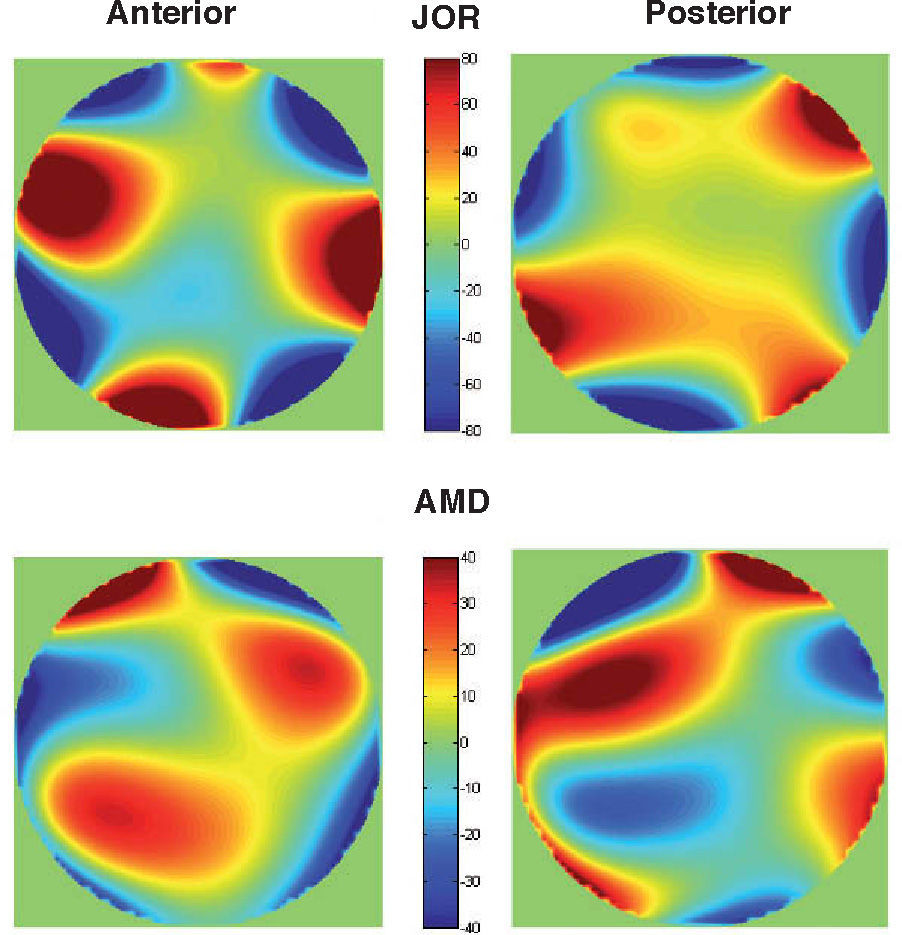
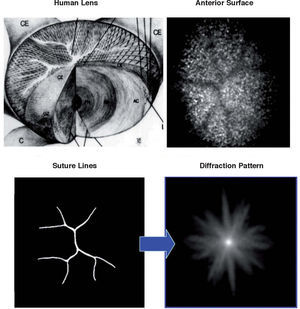
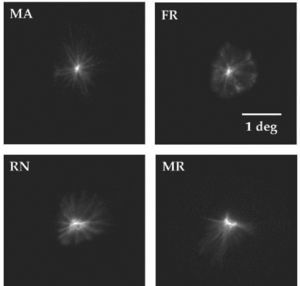
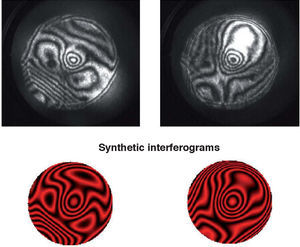
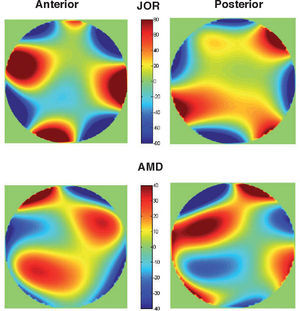
Diffraction is the second factor affecting lens quality. Suture lines of the lens are transparent structures formed by the union of lens fibres, which grow from the periphery to the centre of the lens. Figure 7 shows a simple model,72 which could explain the well-known phenomenon of star images by diffraction at the suture lines. The top-left panel displays a diagram of the lens fibres and suture lines; on the right, a coherent image of the anterior lens surface shows the subcapsular epithelium with a ground glass appearance, and shadows caused by the sutures.73 These sutures are transparent objects which could affect light propagation; i.e. they diffract the incident wavefront. The lower panels show a diffraction model: On the left we can see a typical pattern of suture lines, here considered as a phase object (black means zero phase and white is a phase different from zero; π/2 in this example). Assuming a circular pupil, the resulting PSF (point spread function; lower-right panel) displays a beautiful star shape. Therefore, diffraction at the suture lines of the lens might cause star images. Figure 8 shows objectively recorded monochromatic retinal star images, PSF, for four subjects. These star images are formed by the optical system of the eye (cornea and lens) through a fully dilated pupil. Their shape is different for each subject, as a result of the combined effect of diffraction, aberrations and scattering (low but visible in these images). Finally, optical aberrations are the most important factors affecting optical quality. Again direct measurements of the optical aberrations of the lens74 are scarce. Macaque and pig lenses75 seem to have large amounts of spherical aberration (both 4th- and 6th-order), astigmatism, coma and trefoil. Figure 9 shows wavefronts obtained in two samples of pig lenses.76 Again, most of these in vitro studies correspond to non-human lenses; published in vivo measurements are always indirect;77-79 so that there is a large uncertainty on the contribution of the lens to the optical quality of the eye. There are too many unknowns to measure and model the crystalline lens. As in the cornea, the surface topographies are essential, but they are extremely difficult to measure with accuracy and enough resolution. One indirect way is to retrieve plausible topographies adjusted to fit optical performance in custom eye models. Figure 10 displays anterior and posterior (left and right) topographies obtained for two subjects (JOR, upper panels; AMD lower panels).22 Even though these topographies are no real measurements, and have been estimated under several assumptions and approximations, their general appearance is highly illustrative. As compared to the cornea, these topographies display trefoil, and mainly tetrafoil (more marked for JOR), which could be related to the fibrous structure of the lens and, in particular, to the pattern of suture lines.
Retinal images of point objects (PSF) recorded in vivo. These images display different pattern star images for each observer. Subject MA shows a high similarity with the computed pattern (see figure 7).
In summary, the lens is a highly complex and dynamic optical element. Its changes with age and accommodation, including mechanical behaviour, make it difficult to extrapolate data from in vitro to in vivo, or from one condition to another (time, accommodation, etc.) We know some essential features, but despite the high number of studies published in the literature, the number of unknowns is still too high, thus precluding an accurate modelling (either custom or generic).
The Optical System of the EyeOptical System ComponentsThe optical system of the eye results from the combination of the two main refractive elements, cornea and lens, the iris diaphragm, and the retina, with their respective relative positions and orientations in the 3D space (axes).
PupilThe entrance and exit pupils (images of the iris in the object and image space respectively) have a crucial role in image and vision quality. With high light (photopic) levels the pupil size is small, thus stopping peripheral rays, which are typically more aberrated. For low light levels, the number of photons is also low and the signal-to-noise ratio decreases due to quantum noise. Then the pupil dilates to increase the number of photons. In this way the pupil can balance optical blur and noise to obtain an optimal trade-off between these two major factors affecting the quality of vision. The position of the pupil either along Z (visual axis), or X, Y decentrations has a strong impact on optical aberrations, especially coma. The position z of the pupil controls the off-axis performance of an optical system, including aberrations (coma, oblique astigmatism, field curvature), vignetting, etc. The position of the iris close to the lens permits to avoid vignetting for very wide field angles. The pupil is often displaced nasally (about 0.5mm) with respect to the optical axis,51 which should have an effect on aberrations (coma in particular).
RetinaThe retina has a two-fold role in the optical design of the eye. As it will be explained later, the curvature of the retina seems to match closely the image curvature, which has a major impact in maintaining a reasonable peripheral image quality.15 In addition, each retinal cone from the mosaic of photoreceptors, behaves as an individual waveguide. These waveguides approximately point to the centre of the pupil and have a limited acceptance angle. As a consequence, the relative efficiency of the rays reaching one photoreceptor is maximum for the chief-ray (ray connecting the centre of the pupil with the centre of the waveguide) and decreases for peripheral rays (higher aperture angles). This is the well-known Stiles-Crawford effect, which is a sort of pupil apodization.80 The reduced luminous efficiency of peripheral rays attenuates aberrations of peripheral rays, as well as the effect of intraocular scattering. In summary, the retina is a fundamental component of the optical system of the eye and plays an essential role in the optimization of its performance, both on-axis by waveguiding and off-axis by means of its curvature.
AxesAnother feature of the optical system of the eye is that there is no common axis. Each surface or optical component (from the anterior surface of the cornea, to each individual photoreceptor) has its own axis of symmetry. In general, surfaces have no revolution symmetry. Within a reasonable approximation, one can consider 3 orthogonal axes in the 3D space for each surface (as in Eq. 2). The axis closer (minimum angle) to the Z axis can be considered to be the optical axis of each surface or element. The lack of symmetry of the surfaces and/or optical elements, decentrations, misalignments and deformations (i.e. Zernike deformation modes) will contribute to increasing HOA and, in general, to a deterioration of the optical quality.
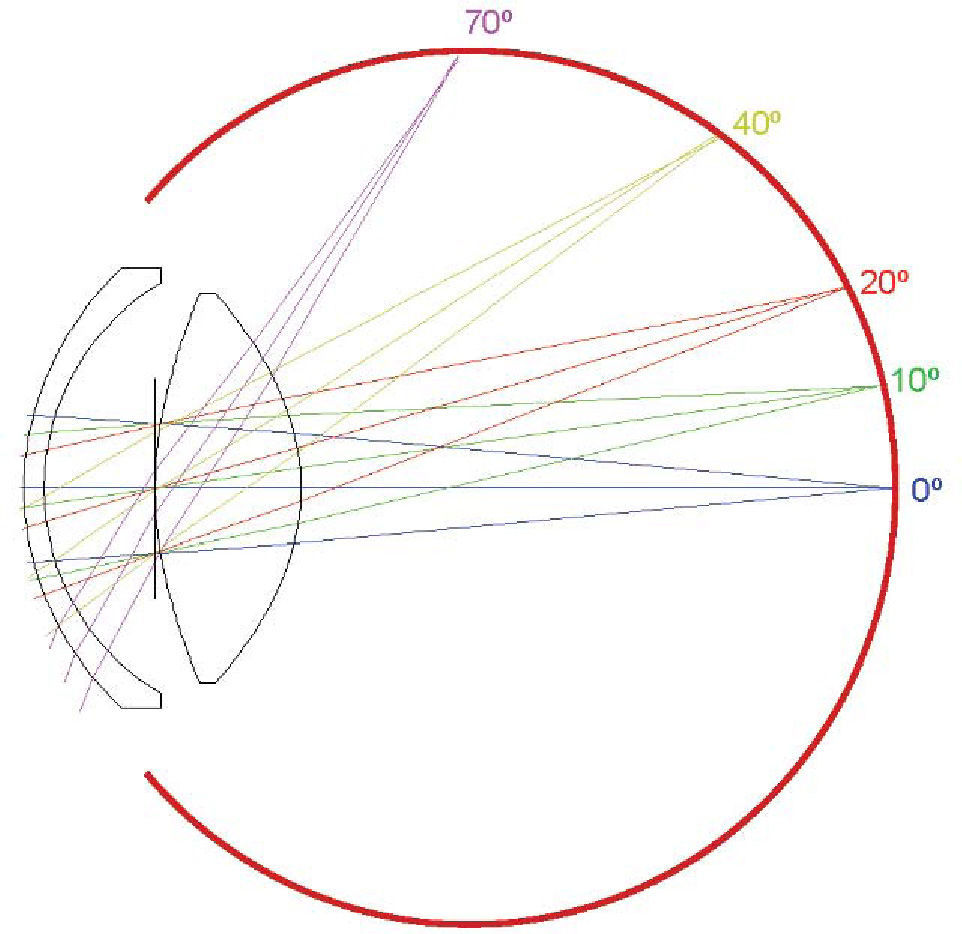
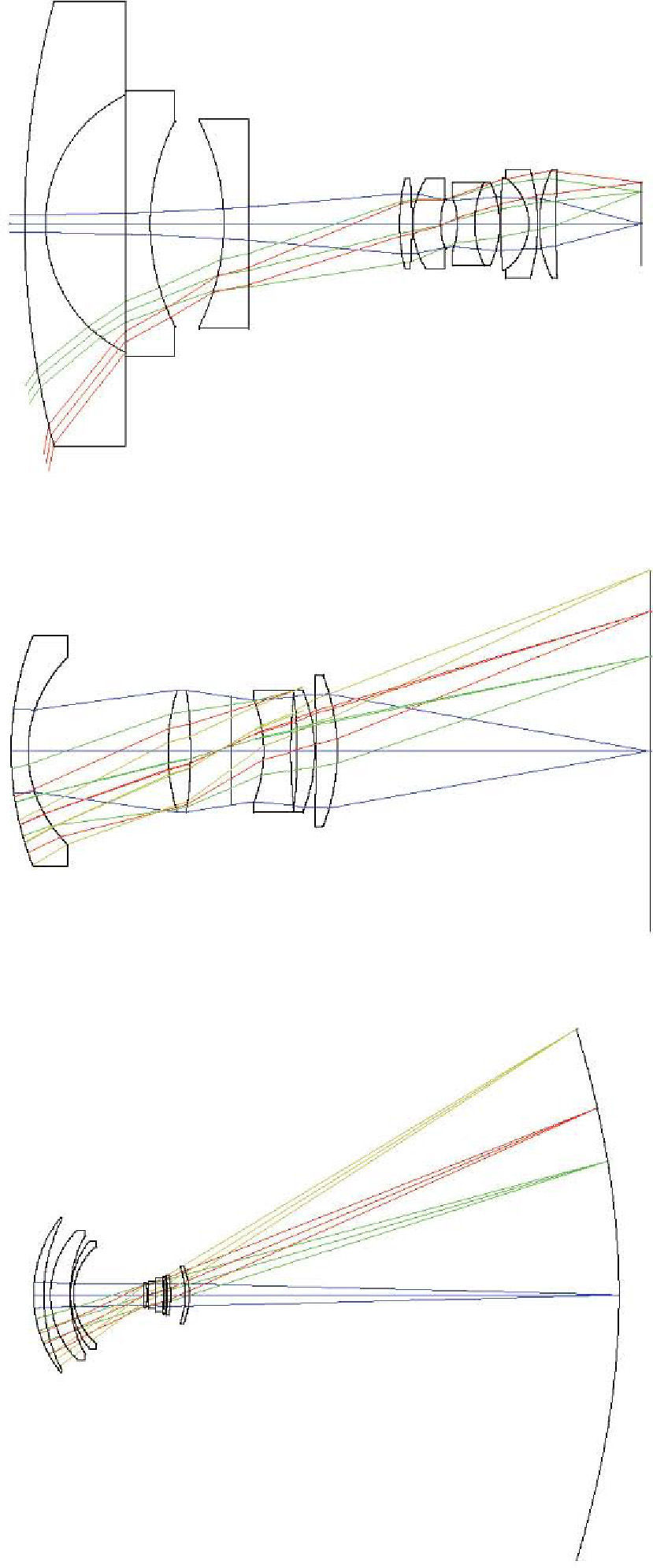
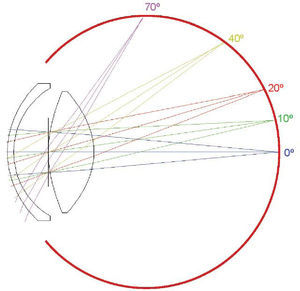
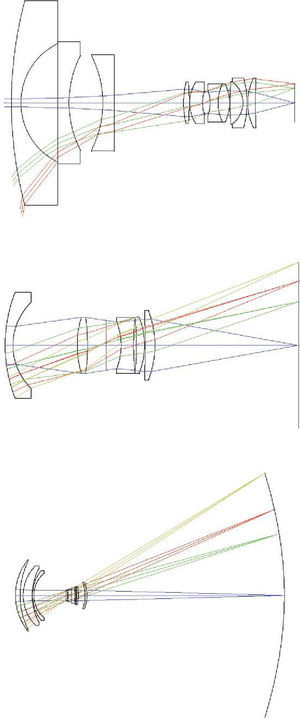
Optical DesignFigure 11 depicts a schematic diagram of the optical system of the eye. The first compelling evidence is that it is a very-wide-angle system.12,14,15,19 The figure shows results of ray-tracing up to 70° of semifield, but the total field is about 180° (90° semifield). Many analogies between the human eye and wide-angle lenses can be found in the optical design literature. Wide-angle optical systems usually have two groups of lenses with an arrangement which resembles that of the human eye, no matter the application (projection, photography, etc.). Figure 12 displays 3 representative examples that cover the main types of wide-angle systems and applications. The first example (upper panel) is a 160° projection lens;81 the second (central panel) is an inverse tele-photo (US Patent #4203653); and the third (lower panel) is a double Gauss objective (US Patent #4832472 modified). We can see some features common to all of them: in all cases, the first lens is a meniscus (or group) with a high aperture in order to collect light from wide angles; the diaphragm is in front or within the second group of lenses; this second group is more complex (more surfaces) but smaller in diameter; and all these designs try to follow (to some extent) the symmetry principle (more patent in the double Gauss objective, lower panel). There are also outstanding differences: in the first example (upper panel) the system transforms the object wide field into a small flat image. We can see that the initial field angles are strongly reduced at the output. This is difficult to achieve and, as a result, this system is more complex, with a high number of lenses and the numerical aperture of each beam (labelled by different colour) being small. In the second example, the image is flat again, but field angles are reduced only slightly with the benefit of requiring less lenses and allowing a higher aperture. Finally, the double Gauss is a highly symmetric design, which reduces even less the field angles and forms a curved image to keep very wide angles in focus.
If we now compare those designs with the human eye (Figure 11) we can find several analogies but also differences in design principles or strategies. The first difference is that the two groups of lenses in the artificial designs are just single lenses in the eye. However, the crystalline lens is more complex than a single lens since it has nucleus and cortex. In addition, it has a GRIN structure (mainly in the cortex) and aspherical surfaces. Aspherical surfaces are often used to reduce the number of lenses, because a single asphere can correct several aberrations, especially spherical, astigmatism and distortion.82 Another simplifying strategy in the eye is to leave chromatic aberration uncorrected. In fact, it has been shown that the LCA (longitudinal chromatic aberration) of the eye is close to that of a salty water single-surface lens.8 In lens design, CA is corrected by a combination of glasses with low and high dispersions (the classic flint & crown), but this strategy is difficult with biological tissues having a high water content. Thus, nature doesn’t seem to even try this hardly achievable goal. This strategy permits a simpler design saving lenses.
Nevertheless, eye's design is not as simple as one may think. The lens can be modelled as a cemented triplet; i.e. the biconvex nucleus sandwiched by two cortical meniscus. In addition, the lens surfaces are highly aspherical (hyperbolas) and the lens cortex has a GRIN structure. Therefore the complexity of the human lens could be comparable to the second group of lenses of the examples. We can apply a similar reasoning to the corneal meniscus. It would be equivalent to a group of lenses in an artificial design because of its aspheric surfaces (and absence of correction of CA.)
One of the most important strategies used by lens designers is the so-called symmetrical principle.82 A completely symmetrical optical system is free of coma, distortion and TCA (transverse chromatic aberration or lateral colour). Of course this is only a starting principle and symmetry can only be approximated in real systems. The application of the principle is to depart from a highly symmetric system, and to gradually adapt and optimize it for a particular application. The initial symmetry is progressively broken in this process, so that in the final system only traces of the initial symmetry can be observed. Nevertheless, this principle underlies all wide-angle-lens designs (more patent in the third example) of figure 12. Despite the lack of symmetry in the human eye, the symmetrical principle is manifest in several aspects: the biconvex lens (triplet) is highly symmetric. Optimization through evolution has slightly broken such symmetry so that the back surface is more curved than the anterior one. Regarding the complete optical system, we can observe additional traces of the symmetrical principle in figure 11. The iris diaphragm is placed close to the geometrical centre of the cornea-lens system; if we consider the two most powerful surfaces, first and last (neglecting, in a first approximation, the two intermediate surfaces, which have much less refractive power), then we have a symmetrical optical system with the diaphragm in the centre. Therefore, the eye's optical system follows the symmetrical principle which is the most powerful strategy to have a very wide-angle field. Taking into account the refractive indexes of the ocular media, and the relative dioptric power of each surface, the presence of this principle is manifest.
In summary, the symmetry principle is present in (i) the design of the lens, (ii) the combination of cornea and lens and (iii) the placement of the iris. On the contrary, we have other three opposite features, which result in a lack symmetry of the OS (optical surfaces): (i) non-revolution symmetry OS, (ii) OS deformations and (iii) misalignments and decentrations between both eyes.
It is worth noting, however, that non-rotationally symmetric design principles based on an eccentric pupil and off-axis aspherical mirrors have been proposed for large wide-field telescopes. Korsh telescopes, having 2, 3 or 4 mirrors, depending on the particular version, are anastigmats, aplanatic and provide flat-field images;83 in particular the TMA (three mirror anastigmat) is a good example. Consequently, pupil decentration, misalignments and eccentric (non-rotationally symmetric) surfaces might reflect some smart design strategy rather than a design flaw. A plausible explanation is offered later.
Optical Performance: DataThe optical design discussed above predicts several distinctive features of the eye. Such a design matches that of a verywide-angle lens. The main predictions of this design are:
- -
LCA is uncorrected
- -
Spherical aberration might be corrected or moderated by aspherical (conicoid) surfaces;
- -
Coma might be low due to symmetrical principle (including iris location);
- -
Astigmatism is present due to non-rotational symmetry (toricity). Oblique astigmatism is moderated by conicoid surfaces, but can reach huge values for peripheral fields;
- -
Surface deformations, tilts and misalignments might cause HOA (trefoil, tetrafoil, 4th-order astigmatism, etc.)
- -
Image curvature may match retinal curvature, keeping peripheral defocus under reasonable limits.
- -
Distortion is not an issue as there is a highly non-uniform cortical projection84 and the brain might learn to calibrate distortions when analyzing images (as with the inverted image).
- -
Scattering is minimised (in young eyes) by design and its effect is even lower due to the presence of waveguide photoreceptors.
- -
Lens structure (suture lines) may cause diffraction as well as HOA (trefoil, tetrafoil, etc.)
The eye is more myopic (> 1 D) for the shortest wavelengths (blue) and hyperopic for long wavelengths (> 0.5 D). The total chromatic difference of focus, LCA, is about 2 D within the visible spectrum.85 LCA shows low intersubject variability and good agreement between model predictions and experimental data.7,8 On the contrary, TCA varies among subjects86,87 and is hardly predicted by rotationally symmetric eye models.
Monochromatic High Order AberrationsThe human eye is known to have important amounts of HOA. Roughly speaking, the RMS wavefront error for pupils of about 6.5mm is of the order of λ (one wavelength). Similarly to other optical systems, ocular HOA increase substantially with pupil diameter. In fact, the rate of increase for each aberration mode is given by the order of the corresponding Zernike polynomial. For instance, spherical aberration (4th-order) will increase with pupil diameter faster than coma or trefoil (3rd-order). Aberrations also increase with age. Applegate and co-workers88 have found the following empirical law for the change of the average RMS wavefront error W as a function of age A (years) and pupil diameter Dp (mm):
The aberration pattern shows a wide intersubject variability (the specific pattern of the wave aberration of an individual seems to be quite a personal distinctive feature), while the total amount (RMS error) is somewhat more uniform across the population. HOA also change with accommodation. Recent studies suggest that monochromatic HOA increase monotonically with accommodation, except for 4th-order spherical aberration, which shows the opposite trend89 and eventually cancels or even undergoes a change in sign for strong accommodations. Regarding the distribution of Zernike modes in normal eyes, the magnitude of aberrations decreases monotonically with order.90 This means that the sum of RMS related to third-order aberrations is usually higher than that for fourth-order ones and so forth. Similarly, for a given order n, the magnitude of aberrations also decays with the azimuthal frequency m.91 After applying these rules, it is patent that coma, trefoil and spherical aberration are the most important HOA in the eye, and these three present similar average values.88 The remaining 4th-order modes, tetrafoil, 4th-order astigmatism and again 6th-order spherical aberration have lower but significant average values.
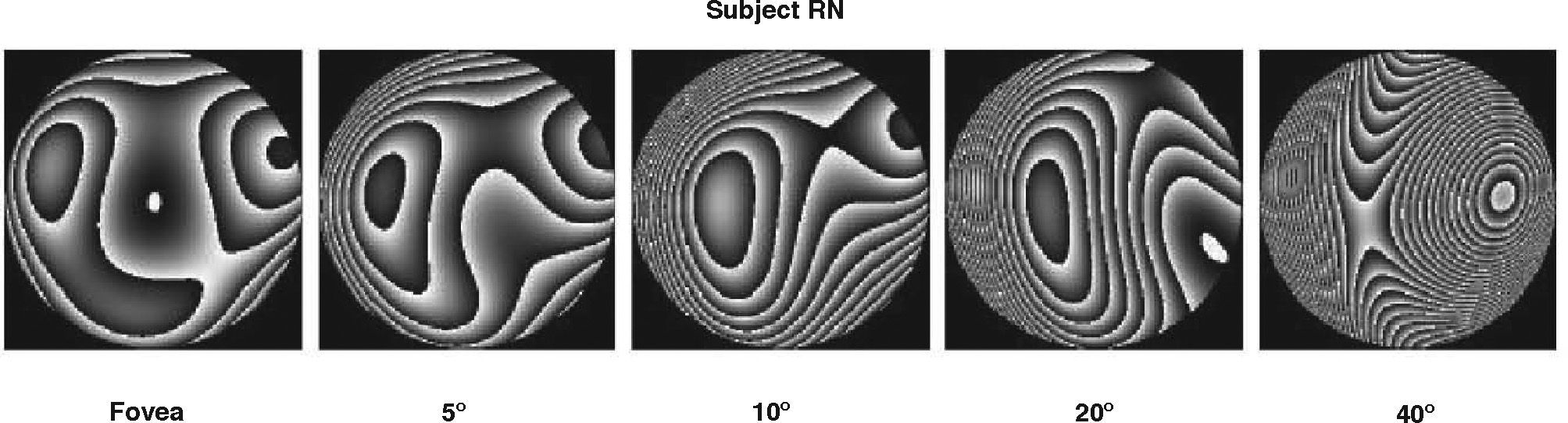
HOA increase with visual field, but less rapidly than in conventional optical systems. It has been found that in the human eye the RMS due to HOA increase roughly linearly from 0° to 40° of eccentricity.92 The rate of increase with visual angle is such that the RMS at 40° is double than the foveal (0°) value. Figure 13 shows how of the wave aberration increases with visual field (along the horizontal meridian) for the right eye of the author.
To analyze these optical-quality data we can apply standard criteria from the optics literature. The wavefront version of Lord Rayleigh's criterion states that the maximum value of the wavefront error must be less that λ/4 (peak-to-valley) to keep a diffraction-limited resolution. More useful is Marèchal's criterion (also known as the λ/14 criterion) for the RMS wavefron error. Under this criterion, and after Eq. 8, the human eye is far from being a diffraction-limited optical system. To meet the λ/14 (with λ=555nm) criterion we have to consider pupil diameters Dp<3mm and very young subjects, unaccommodated and only for the central field. All these variables (pupil diameter, age, accommodation and visual field) have a strong impact on aberrations and, hence, we can consider that in most circumstances and for most subjects the quality of the eye is far from the diffraction limit.
Defocus and AstigmatismThe above analysis is only valid for HOA. This means that it is only valid for monochromatic light and strictly emmetropic subjects. However, following the above statistical (empirical) laws of distribution of Zernike modes, it turns out that the main contributions to the wavefront error are second-order Zernike modes: defocus and astigmatism. These errors can be compensated by lenses, but second order is the one with the highest contribution to the total wavefront error. The prevalence of myopia is quite high in the population and the average astigmatism is of nearly 0.5 D.93 These 2nd-order aberrations also increase with visual field.94
Model PredictionsSchematic generic models published until now were extremely useful for explaining first-order (Gaussian) properties of the eye;4 overall peripheral performance (oblique astigmatism,11 field curvature, etc.15) and LCA.7,8 However, they were strongly limited to analyze some of the key design features or irregular HOA. As an example, we can compare two kinds of models: optimized versus anatomical (no optimized parameters). Some non-optimized models provide a good overall agreement with the RMS HOA, but due to their rotational symmetry, the only predicted contribution to the RMS is due to spherical aberration.7 This means an overestimation of SA. On the contrary, other models (optimized by adjusting conic constants) provide a better estimate of spherical aberration,5 but then the total RMS is underestimated. As a result, these eyes predict a much better optical quality than that found in real eyes, where astigmatism, coma or trefoil may have similar or higher values. It is patent that a realistic model must incorporate misalignments, decentrations, lacks of rotational symmetry and surface deformation modes, such as in the analysis of the cornea in section “Optics of the Human Cornea”.
Models have shown to be useful to predict the compensation of corneal aberrations by the lens (or internal optics) which has been found experimentally.30,95,96 Almost any schematic model predicts a partial compensation, because the signs of the SA of the corneal meniscus and the biconvex lens are opposite (as a result of the symmetry principle). Nevertheless, models with conic surfaces make a better prediction.7
Much work has been done on the optical significance of the GRIN distribution of the lens, but with a high degree of uncertainty and speculation due to the lack of experimental data. As discussed above, quadratic distribution models tend to overestimate the impact of the GRIN distribution, whereas anatomical GRIN profiles suggest a refractive index almost homogenous in the nucleus and mainly distributed within the cortex.63,65 Different types of GRIN distributions yield totally different predictions27,29 of optical performance. More recent studies,68,69 suggest that the contribution of the GRIN distribution to the optical performance of the eye may be modest compared to earlier assumptions.
Our current knowledge and state of the art in measuring techniques often lead to paradoxical mismatches between experimental data and model predictions. The lens paradox is a clear classic example. It refers to emmetropia remaining rather constant with age, despite the marked increase in surface lens curvatures.97 Experimental evidences of accommodation, aging and presbiopia studies suggest that the aging lens may correspond to a sort of accommodated state (thicker and more curved lens), so that presbiopia could be interpreted as the decline of the ability to desaccommodate rather than to accommodate. If the aging lens is always accommodated, then the eye should be myopic and this is not the case (lens paradox.) Most explanations of this paradox rely on the change of the GRIN distribution with age, but there are other factors, such as lens growth and other potential changes of the optical system of the eye. It is clear that paradoxes like this must come from too simplistic or wrong models and assumptions, added to the lack of experimental data. The effects of aging (lens paradox, decline of optical quality, presbiopia) are showing to be especially difficult to model (Navarro R, et al. IOVS 2008;49:ARVO E-Abstract 4027).
Concluding RemarksIn summary, even for best-corrected optical performance (only HOA), the eye is highly aberrated except for small pupils (Dp<3mm), young subjects, on-axis and under monochromatic illumination. Without optical correction (spectacles, contact lenses, etc.), the contribution of astigmatism and defocus will substantially increase the wave aberration. As a result, and in white light illumination, the naked eye with natural physiological pupil sizes is far from being diffraction limited. In addition, many experimental evidences88,98-100 suggest an approximately monotonic decline of optical quality with aging. Different authors judged quite differently the design and optical performance of the eye. For instance, Von Helmholtz4 would not accept a lens with the optical defects of the eye; whereas for Artal et al.101 the eye is an example of robust design. These apparently opposite comments reflect the paradoxical mixture of flaws and smart design principles and optical performance that the human eye exhibits; for example the symmetrical principle together with the total lack of symmetry of the optical surfaces and misalignment of the axes. With these “paradoxes” it is relatively simple to conciliate opposite comments regarding the eye. For instance a smart design principle (such as symmetry) with a poor optimization and implementation (lack of symmetry) will display large optical defects;4 but this turns out to be robust101 simply because the optical quality is poor enough to get much worse. Nevertheless, one might argue that the optical design of the eye is not too bad considering that its optical quality worsen when it is modified, for instance by surgery. Many scientific studies have consistently demonstrated an increase of aberrations and a decrease of optical quality after cataract102 and refractive103 surgery. Novel designs of intraocular lenses or custom LASIK treatments have not been able to beat the modest quality of the biological optical system of the eye until now.
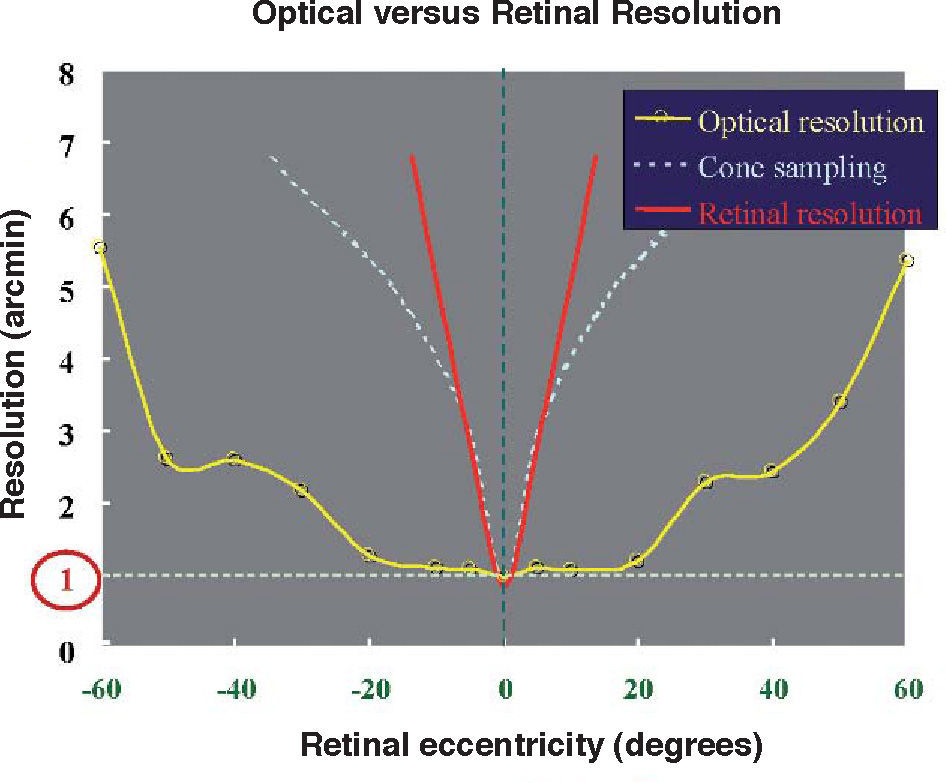
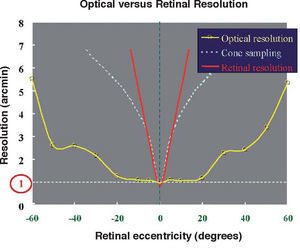
By taking all aberrometric data of the eye together, and comparing them to the quality of manmade optical systems a surprising conclusion is obtained: on-axis the optical quality of the eye is modest, but quality declines less rapidly with visual field. As a consequence, the optical quality of the eye is more homogeneous across visual field than that of conventional optical systems.104Figure 14 compares the different resolutions of the optical system (yellow), the sampling by the cone mosaic (light blue) and the effective retinal resolution (red) related to the density of ganglion cells.
Apparently, this is an astounding flaw of design for a foveated, highly inhomogeneous retinal sampling105 and cortical magnification factor.84 In other words, there is a good match between optical resolution and retinal resolution at the fovea, but there is a rapidly increasing mismatch towards the peripheral visual field. The reason is that the rate at which optical resolution decreases with eccentricity is low, whereas retino-cortical resolution worsens dramatically.104,105 This seems to be a paradoxical design flaw, difficult to explain and one may only conjecture some hypotheses. I like, but could never proof, the following explanation among other possibilities: If one analyzes visual systems in nature, one finds that very wide-angle eyes, often covering 180° is the dominant design, especially in insects (compound eyes) and vertebrates (single optics). A subgroup of vertebrates (predators, birds, primates, etc.) has developed foveated vision. It looks like that wide angle perception is necessary for more basic functions, such as defence and locomotion (or navigation), while the fovea has a more specialized function for high-resolution demanding tasks, predation or detection of far objects (birds). Perhaps, having good peripheral optics has been essential for survival. Then, when the fovea appeared later in evolution (with its associated high retinal inhomogeneity), the optics could possibly need only minor adjustments and adaptations. Related to that, one may also conjecture possible reasons for the lack of rotational symmetry. Intuitively, the displacement of the fovea with respect to the “nominal” optical axis (about 5° temporal) might require some optical adaptation. Among the different possibilities, a safe and relatively simple strategy is to increase the homogeneity of the optical quality in the central field (<10°), at the cost of loosing quality on the optical axis, which is not needed anymore. This may justify eccentric, off-axis, nonrevolution surfaces (as in TMR wide angle telescopes).
In conclusion, the optical system of the eye seems to combine smart design principles with outstanding flaws. Figure 3 is especially illustrative. The corneal ellipsoid shows a superb optical quality on axis, but in addition to astigmatism, it is misaligned, deformed and displaced with respect to the pupil. All these “flaws” do contribute to deteriorate the final optical quality of the cornea. Somehow, there could have been an opportunity (in the evolution) to have much better quality, but this was irreparably lost. Until now, such a modest quality could not be improved by surgery; indeed, any attempt of modification, and ageing itself, only yields a reduction of the optical performance.
This research was supported by the Spanish CICyT, grant FIS2008-00697.