To conduct a clinical validation of a virtual reality-based experimental system that is able to assess the spherical subjective refraction simplifying the methodology of ocular refraction.
MethodsFor the agreement assessment, spherical refraction measurements were obtained from 104 eyes of 52 subjects using three different methods: subjectively with the experimental prototype (Subj.E) and the classical subjective refraction (Subj.C); and objectively with the WAM-5500 autorefractor (WAM). To evaluate precision (intra- and inter-observer variability) of each refractive tool independently, 26 eyes were measured in four occasions.
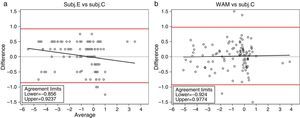
ResultsWith regard to agreement, the mean difference (±SD) for the spherical equivalent (M) between the new experimental subjective method (Subj.E) and the classical subjective refraction (Subj.C) was −0.034D (±0.454D). The corresponding 95% Limits of Agreement (LoA) were (−0.856D, 0.924D). In relation to precision, intra-observer mean difference for the M component was 0.034±0.195D for the Subj.C, 0.015±0.177D for the WAM and 0.072±0.197D for the Subj.E. Inter-observer variability showed worse precision values, although still clinically valid (below 0.25D) in all instruments.
ConclusionsThe spherical equivalent obtained with the new experimental system was precise and in good agreement with the classical subjective routine. The algorithm implemented in this new system and its optical configuration has been shown to be a first valid step for spherical error correction in a semiautomated way.
Objetivo: Realizar una validación clínica de un sistema experimental basado en realidad virtual, capaz de evaluar la refracción subjetiva esférica simplificando la metodología de la refracción ocular.
MétodosPara evaluar la concordancia, se obtuvieron mediciones de la refracción esférica de 104 ojos pertenecientes a 52 sujetos, utilizando tres métodos diferentes: subjetivamente con el prototipo experimental (Subj.E) y la refracción subjetiva clásica (Subj.C); y objetivamente con el autorrefractómetro WAM-5500 (WAM). Para evaluar la precisión (variabilidad intra e inter observador) de cada herramienta refractiva, de forma independiente, se midieron 26 ojos en cuatro ocasiones.
ResultadosCon respecto a la concordancia, la diferencia media (±DE) para el equivalente esférico (M) entre el nuevo método subjetivo experimental (Subj.E) y la refracción subjetiva clásica (Subj.C) fue de −0,034D (±0,454D). El 95% correspondiente a los Límites de la Concordancia (LoA) fue de (−0,856D, 0,924D). En relación a la precisión, la diferencia media intra observador para el componente M fue de 0,034±0,195D para Subj.C, 0,015±0,177D para WAM y 0,072±0,197D para Subj.E. La variabilidad inter observador reflejó peores valores de precisión, aunque fueron clínicamente válidos (inferiores a 0,25D) en todos los instrumentos.
ConclusionesEl equivalente esférico obtenido con el nuevo sistema experimental fue preciso y guardó consonancia con la rutina subjetiva clásica. El algoritmo introducido en este nuevo sistema, y su configuración óptica, han demostrado ser un avance válido para la corrección del error esférico de modo semi-automático.
The measurement of the refractive error of the eye is probably the most common test in the optometric practice. Monocular objective refraction measurements can be currently obtained fast and easily with autorefractors and wavefront aberrometers and they are often used as a starting point for classical subjective refraction.1–4 Several studies have reported that most modern objective refractometers are reliable and accurate in relation with subjective refraction1–13 and, whereas in subjective refraction only one measurement is taken, the average of several objective refraction measurements can be obtained in a fraction of a second, which improves the precision of the outcomes. However, prescribing from objective findings alone achieves limited patient satisfaction2,5 and visual acuity does not improve sufficiently.12 On the one hand, many commercially available autorefractors work in a monocular closed-view environment, which can induce instrument myopia,14–17 a permanent state of overaccommodation that can range from 0.50D to 5.00D.14 On the other hand, binocular open-view autorefractors partially solve this problem1–4,18 although differences with the classical subjective refraction are still important, as they do not consider neural processes and binocular balance. This is probably the main reason why the classical subjective refraction is so far considered the gold standard method for determining the refractive state of the eye although it is linked to a high inherent inter-observer variability.
Nonetheless, it has been reported that the reproducibility (i.e., inter-examiner repeatability) of subjective refraction is not as good as autorefractors or wavefront aberrometers. Bullimore et al.9 found a mean spherical difference between five averaged automated refractor readings, taken by two different optometrists, of +0.02D. When subjective refraction was compared this difference increased up to −0.12D. Pesudovs et al.10 also found that most of objective refractions were more repeatable across clinicians than subjective refraction, and they obtained an interexaminer 95% LoA of about ±0.25D and ±0.50D for objective and subjective refraction, respectively. Other authors came to similar findings and reported precision values of subjective refraction poorer than the objective ones.19,20 Remarkably, MacKenzie21 studied the sphero-cylindrical refractions provided by 40 optometrists and a 95% reproducibility limits of 0.78D was found.
Thus, there are objective refraction systems very precise but not fully equivalent to the subjective classical refraction, and at the same time, the subjective classical refraction is not as reproducible as objective techniques. It is therefore reasonable to think that a good refractive system should mix both methodologies. Accordingly, in this study we present an experimental setup based on a virtual reality system that comprises an algorithm to perform the subjective eye's refraction reducing the interaction of the patient with the examiner and thus simplifying the methodology of refraction.
This study is therefore focused on providing at least a subjective spherical refraction equivalent with the standard procedures in terms of agreement and precision. For this purpose, a clinical validation of the spherical refraction obtained using the experimental prototype (Subj.E) in non-cyclopleged eyes is compared with the classical subjective refraction routine (Subj.C) and the Grand Seiko WAM-5500 (WAM) autorefractor. It is also remarkable that the development of a subjective refractive method in a binocular virtual reality system might be of a great importance from the perspective of integrating a full refractive system with objective (e.g., a Hartmann–Shack aberrometer) and subjective means in a multimodal device.
Material and methodsThis prospective study was conducted on healthy subjects mainly recruited from the staff and students of the Center for Sensors, Instruments and Systems Development (CD6) of the Universitat Politècnica de Catalunya (UPC). The study was approved by the Ethics Committee of the University Hospital Mutua de Terrassa (Barcelona, Spain) and the research followed the tenets of the Declaration of Helsinki. After explaining the nature and possible consequences of the study, written informed consent was obtained from participants. The inclusion criteria for participants were best spectacle-corrected visual acuity of at least 0.1logMAR. All refractions were obtained without cycloplegia and the eye that was measured first was randomly selected.
Agreement with the classical subjective routine (Subj.C) for far distance spherical error was evaluated for the experimental prototype refractive system (Subj.E) and the commercial autorefractometer WAM-5500 (WAM). For each patient, all measurements were conducted in a single session.
Regarding the prototype's precision (i.e., inter-observer and intra-observer repeatability), measurements were compared with those obtained using the WAM and Subj.C. In this case, three clinicians performed randomly the measurements for each patient and one of them was additionally assigned to repeat all the process twice. All measurements were carried out in 4 sessions (1h long each one) during two weeks.
Classical subjective refraction (Subj.C)Streak retinoscopy was firstly performed, followed by subjective refraction with a phoropter and 6 meter Sloan letters chart. Biocular balancing and binocular refinement of the refractive correction to ensure optimal visual performance and patient comfort was then carried out. The maximum plus sphere and minimum minus cylinder consistent with best corrected visual acuity was taken as an endpoint criterion. In this study, classical subjective refraction is considered the reference method for statistical comparisons. It should be remarked that each of the three observers performed the classical subjective refraction besides the other refraction methods.
Objective refraction (WAM)Objective refraction was measured by means of the Gran Seiko Auto Ref/Keratometer WAM-5500 (Grand Seiko Co. Ltd, Japan) and also by a custom-made wavefront refractor based on the Hartmann–Shack technique. It must be noted that since the custom-made wavefront aberrometer is a lab device that has not been validated by an external research group and its validation is not the main purpose of this study, repeatability and agreement of this device are not reported herein.
The WAM is a binocular open-field autorefractor and keratometer able to record eye refraction and pupil size statically and dynamically. The sphero-cylindrical refraction is obtained digitally by analyzing an image of an infrared measurement ring diffused back by the retina. The precision and agreement of this device has already been shown and has been widely used in clinical practice; it is a gold standard of autorefraction.2,22,23
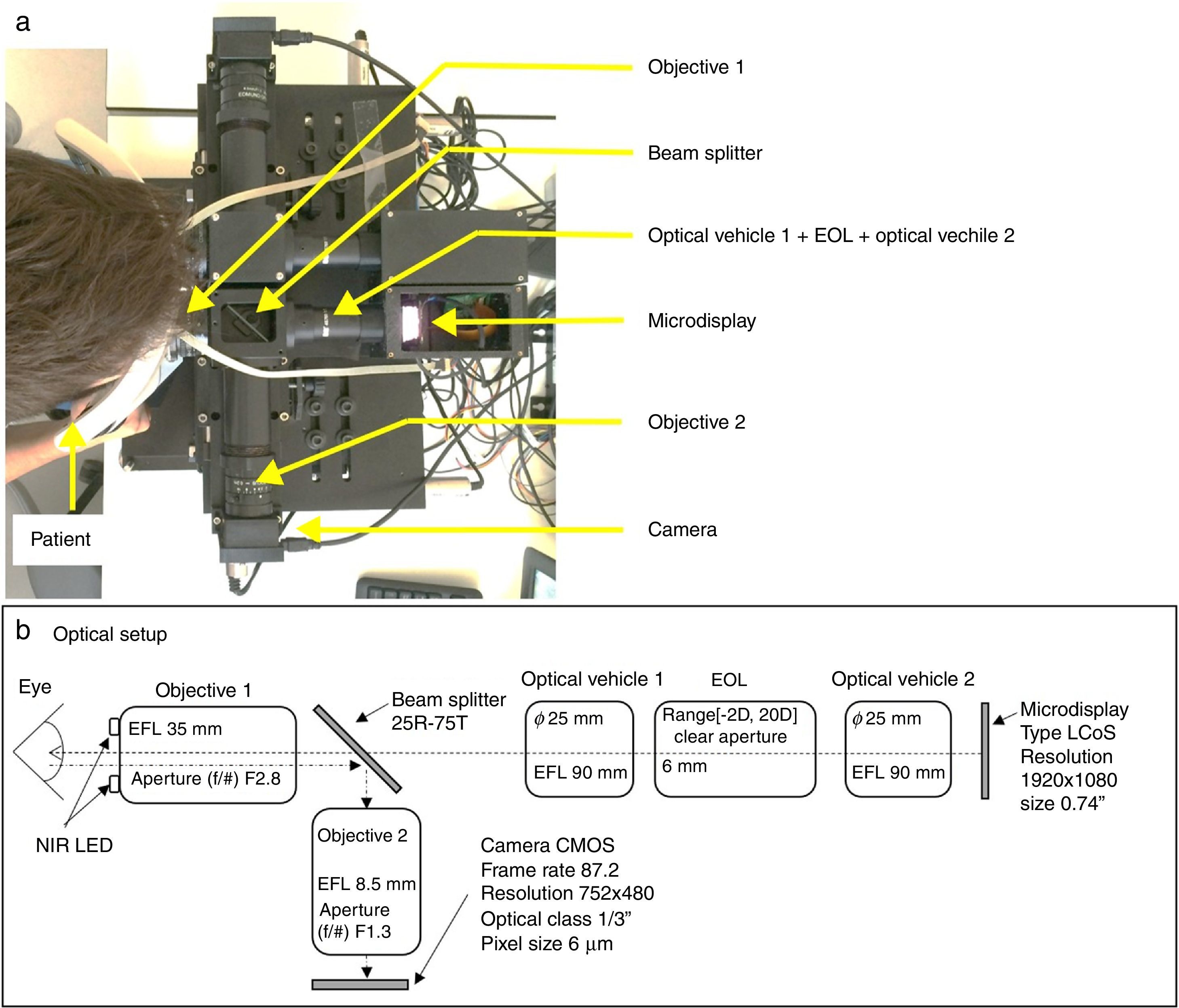
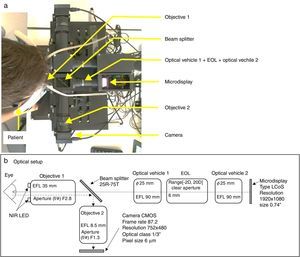
The experimental spherical subjective refraction method (Subj.E)This procedure aims at following the same steps of classical subjective refraction but in a binocular virtual reality environment. The front and top view of the built experimental system can be seen in Figs. 1 and 2a, respectively. A layout with the basic specifications of the optical setup is shown in Fig. 2b. The light coming from the microdisplay (in which the fixation test is shown) is collimated by the optical vehicle 2 and then it goes through the electro-optical lens (EOL)24 that controls the spherical error (it acts as a Badal optometer). After that, light goes through the optical vehicle 1 that projects an intermediate image of the display and finally light is collimated again by the objective 1. The beam splitter that is shown in Fig. 2 partially reflects the infrared (IR) light reflected off the patients’ eye (the IR light sources attached to the objective 1 light the patient's eye) and allows the camera to image the patient's pupil. Notice that the patient's astigmatic refractive error is corrected by means of a trial lens with the cylindrical value obtained with the HS system. The Visual Acuity chart consisted on Sloan letters and lines of letters as small as −0.3logMAR can be displayed with the system.
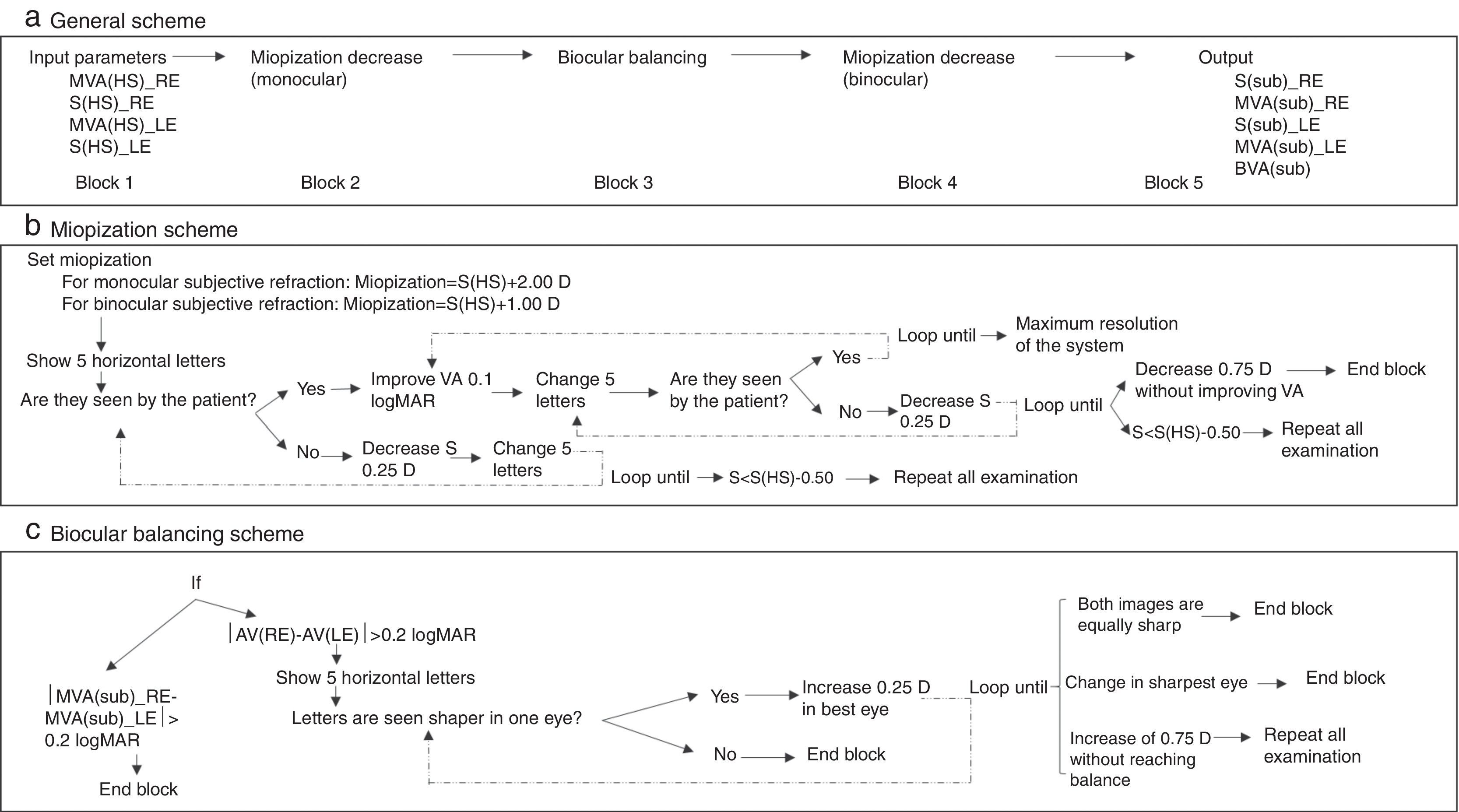
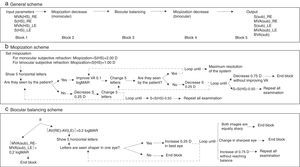
In order to obtain the spherical correction, the following algorithm (Fig. 3) was developed. This algorithm comprises 5 main sequential blocks (Fig. 3a), the first and the last one are devoted to the manual introduction of the input parameters and the printout of the results. The remaining three blocks correspond to the classical three steps of the subjective refraction: monocular subjective refraction; biocular balancing and binocular balancing. The first block requires the introduction of the spherical refraction and its corresponding visual acuity for both eyes. In this study, these input parameters are taken from the objective refraction obtained with the Hartmann–Shack (HS) wavefront measurements. Thus, the HS objective refraction is the starting point of this subjective refraction method. After that, the second block starts running (a simplified diagram of this algorithm is shown in Fig. 3b), which essentially, consists in miopizing the eye to be examined and progressively decrease it in steps of 0.25D in conjunction with an increase of the visual acuity of the stimulus (smaller letters) in steps of 0.1logMAR. Both actions depend on whether the patient is able to see the stimulus (i.e., the 5-horizontal letters) in each loop or not. Notice that this algorithm is actually the same as in the binocular balancing except that the miopization value is set at +2.00D in the monocular subjective refraction and at +1.00D in the binocular balance. Two important aspects of this block 2 are: first, in each loop 5 new random letters appear and the clinician action consists only in pressing the ‘Y’ (Yes) or ‘N’ (No) button according to the ability of the patient to read the letters properly; the second important aspect refers to the ending conditions of the iterative part: in case there is a decrease of 0.75D without improving visual acuity (i.e., the ‘N’ button is pressed three times in a row) the iterative part finishes and returns the maximum plus power achieved with the best visual acuity.
Schematic representation of the spherical refraction algorithm implemented in the experimental prototype. (a) General scheme, (b) diagram of the Miopization part of the algorithm (block 2 and 4), (c) diagram of the biocular balancing part of the algorithm (block 2). MVA(HS)_RE: Maximum Visual Acuity obtained with the Hartmann–Shack refraction in the Right Eye. MVA(HS)_LE: idem for the left eye. S(HS)_RE: Spherical refraction of the Hartmann–Shack measurement in the right eye. S(HS)_LE: idem for the left eye. (sub): Subj.E.
The third block (Fig. 3c) aims at balancing the accommodative state of both eyes and it is carried out only in case the difference in Visual Acuities is less than 0.2logMAR. Otherwise, the classical biocular balancing is carried out: both microdisplays show the same 5 letter stimuli in such a way that one is vertically displaced with respect the other. Thus, a dissociated image is shown and the sharpness is biocularly compared. An increase of +0.25D is induced in the eye's optical path whose image is perceived sharper by the patient. When a change of more than 0.50D is needed, the algorithm stops and the whole process must be repeated. Finally, a binocular balancing is performed (block 4) following the same algorithm as in the monocular case except that in this case the miopization value is set at +1.00D.
Statistical analysisThe statistical analysis was performed using the software SAS System v.9.2 (SAS Institute, Cary, NC, USA) for Windows. All statistical decisions were made at the 5% significance level. The response variable analyzed was the spherical equivalent (M). It is worth mentioning that the classical sphero-cylindrical notation (sphere, cylinder, axis) was transformed for statistical purposes into an orthogonal basis (M, J0, J45) were J0 and J45 are the Jackson cross-cylinders.25 Statistical procedures used data from both eyes for the same subjects since the objective of the study was to compare the performance of several measurement methods and estimate the different sources of variability (measurement error, patient and observer). In this sense all inference results were obtained using linear mixed models considering patient, observer and the interaction between patient and observer (when appropriate) as a random factors.26,27
Regarding the agreement analysis, the spherical equivalent bias between measurements was described using mean difference±the standard deviation (SD). The mean difference was computed as the non-reference method (WAM or Subj.E) minus the classical subjective refraction (Subj.C). The Intra-Class Correlation coefficients (ICC) were obtained to quantify the degree of correspondence between methods using linear mixed models. The agreement was described using Bland and Altman plots. The Limits of Agreement (LoA) were obtained as the 95% confidence limits for the difference between measurements. Additionally, percentages of cases within a given absolute difference (|dif|) were also used to describe the level of concordance.
In the precision analysis, i.e., in order to measure the degree of repeatability (intra-observer) or reproducibility (inter-observer) of the different measurements, the mean difference (±SD) was also used. The ICC coefficients were also calculated and percentages of cases within a given absolute difference (|dif|) were computed to describe the level of concordance.
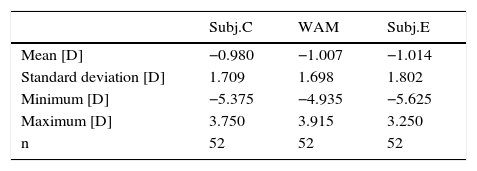
ResultsAgreement52 subjects (22 male and 30 female) were finally included in the study of agreement, ranging in age from 13 to 64 years (mean±SD: 29.6±12.2 years) with a manifest spherical refractive error of −0.74±1.60D (−5.00 to +3.75D) and cylinder of −0.49±0.60D (−3.00D to 0.00D).
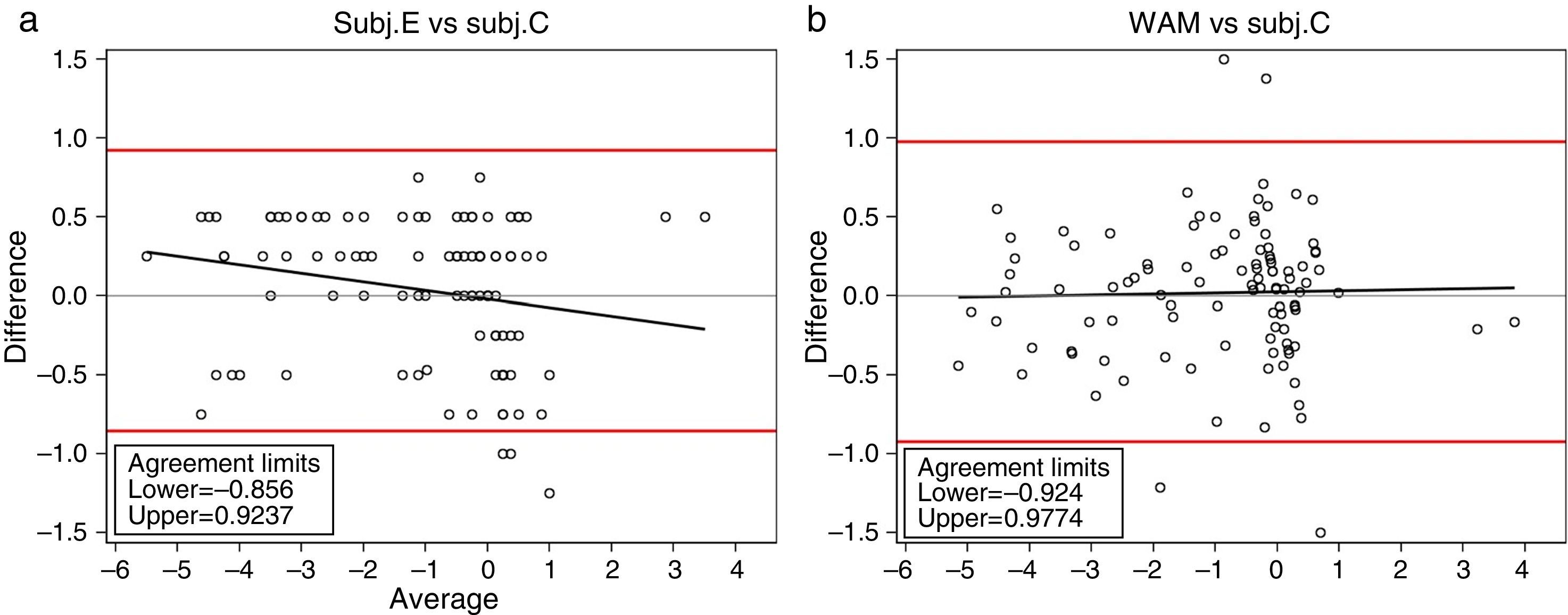
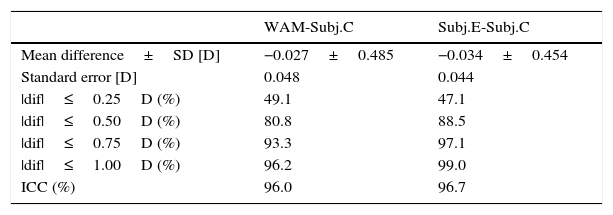
Tables 1 and 2 show the descriptive summary and the pairwise comparisons of each method for the spherical equivalent (M). On average, it can be seen a small myopic shift of each method when they are compared with the classical subjective (Subj.C). The largest bias is obtained for the Subj.E, with a mean value of −0.034D. Besides, the standard deviation of the differences turns out to be similar in all cases although the largest value is obtained when comparing WAM against the classical subjective (±0.049D) (see Bland and Altman plots in Fig. 4). At this point, it has to be noted that since the spherical equivalent of Subj.E is obtained by the cylinder value of the custom-made HS, the comparison between Subj.E and Subj.C might be affected by the HS measurement. Thus, the Jackson cross-cylinders (J0 and J45) obtained by the Subj.C and the HS were compared and the mean difference (±SD) was −0.14D (±0.21D) for the J0 and +0.16D (±0.22D) for the J45. None of these differences turned out to be neither statistically (p<0.05) nor clinically significant. It can be concluded that the effect of the HS on the comparison between the Subj.E and Subj.C is in an acceptable level.
Results of accuracy (agreement) between the WAM-5500 autorefractometer (WAM) and the new experimental system (Subj.E) with respect the classical subjective method (Subj.C) SD: standard deviation, |dif|: absolute difference, ICC: intraclass correlation coefficient, D: diopters.
| WAM-Subj.C | Subj.E-Subj.C | |
|---|---|---|
| Mean difference±SD [D] | −0.027±0.485 | −0.034±0.454 |
| Standard error [D] | 0.048 | 0.044 |
| |dif|≤0.25D (%) | 49.1 | 47.1 |
| |dif|≤0.50D (%) | 80.8 | 88.5 |
| |dif|≤0.75D (%) | 93.3 | 97.1 |
| |dif|≤1.00D (%) | 96.2 | 99.0 |
| ICC (%) | 96.0 | 96.7 |
Regarding the percentage of absolute differences between methods it can be seen that around 50% of the cases are within and absolute difference of less than 0.25D, which is the limit often considered of clinical significance in the optometric practice. Moreover, more than 90% of the cases are within an absolute difference of 0.75D. The Intra-class Correlation Coefficients, which were corrected for the inclusion of both eyes, show values of 96.01% and 96.70% for the WAM and Subj.E respectively when compared with the classical subjective (Subj.C). Even though in all pairwise comparisons good agreement is obtained, i.e. in all cases mean differences are within the limits of clinical significance (<0.25D), it can be seen a slightly worse results for the WAM than for the Subj.E.
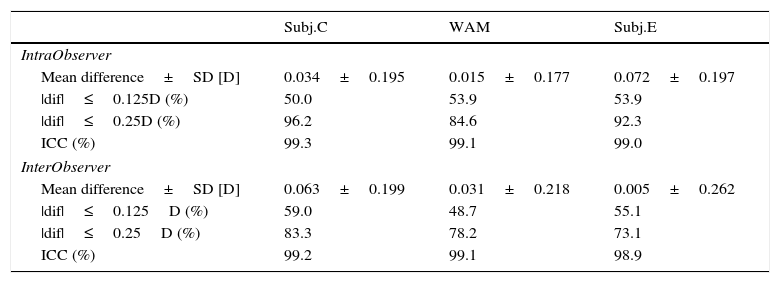
PrecisionTwenty six eyes participated in the study of precision. Age ranged from 23 to 49 years (mean: 36.0±11.3 years) and spherical refraction was comprised between −4.25D and +0.75D (mean: −1.90±1.70D) and cylinder between −1.34D and −0.03D (mean: −0.56±0.40D). Table 3 shows the corresponding repeatability (intra-observer variability) and the reproducibility (inter-observer variability) obtained by means of the classical subjective refraction (Subj.C.), WAM and the experimental subjective method (Subj.E).
Intra- and inter-observer variability for the spherical equivalent (M) obtained with classical subjective refraction (Subj.C), the WAM-5500 autorefractor (WAM) and the new experimental system (Subj.E). SD: standard deviation, ICC: intraclass correlation coefficient, |dif|: absolute differences, D: diopters.
| Subj.C | WAM | Subj.E | |
|---|---|---|---|
| IntraObserver | |||
| Mean difference±SD [D] | 0.034±0.195 | 0.015±0.177 | 0.072±0.197 |
| |dif|≤0.125D (%) | 50.0 | 53.9 | 53.9 |
| |dif|≤0.25D (%) | 96.2 | 84.6 | 92.3 |
| ICC (%) | 99.3 | 99.1 | 99.0 |
| InterObserver | |||
| Mean difference±SD [D] | 0.063±0.199 | 0.031±0.218 | 0.005±0.262 |
| |dif|≤0.125D (%) | 59.0 | 48.7 | 55.1 |
| |dif|≤0.25D (%) | 83.3 | 78.2 | 73.1 |
| ICC (%) | 99.2 | 99.1 | 98.9 |
Intra-observer variability is very similar in all methods, with mean absolute differences below 0.25D. Around 90% of measurements are linked to absolute differences below 0.25D and 100% of them to less than 0.50D. All ICC indexes are above 99%. Regarding inter-observer variability, all mean absolute differences are below 0.25D and again, ICC values are above 99% in all methods. However, when considering the percentages of cases with absolute differences below 0.25D, the WAM and Subj.E drop down to 78.2% and 73.1% respectively whereas the Subj.C have values of 83.3%.
DiscussionThe aim of this study was to show an experimental setup based on a virtual reality system that comprises an algorithm to perform the subjective eye's refraction reducing the interaction of the clinician. The precision and agreement of the spherical equivalent obtained with this experimental prototype was compared to the classical subjective refraction and the WAM autorefractor.
On the one hand, the mean differences with the reference method (Subj.C) were close to zero in all cases: −0.034±0.454D for the Subj.E and −0.027±0.485D for the WAM. The same analysis but using percentages of cases within absolute differences reported that 47.1% of the eyes differed by less than ±0.25D for the Subj.E whereas for the WAM it was 49.1%. Despite these differences with respect the classical subjective refraction, in all cases the limit of clinical significance is not surpassed (i.e., 0.25D). It therefore suggests that all these methods might be equivalent for practical purposes.
However, on the other hand it must be pointed out that we are considering mean values of the whole sample, when clinically we deal with individual patients. Therefore for some individuals these differences can be greater than 0.25D. On the other hand, the standard deviation of the differences in all cases were around ±0.40D and the Limits of Agreement (95% LoA) were not as good as one might expect (Fig. 3); for the Subj.E they were of −0.856–0.924D and for the WAM they were of −0.924–0.977D. These wide LoA can be explained up to some extent due to the inherent variability of the gold standard (the classical subjective refraction), which as Cleary et al.1 stated, must be taken into account. Besides, differences between methods might also be influenced by changes of pupil size during measurements (a more myopic refraction might be found at the periphery) and by different degrees of instrument myopia.16 Typically, conventional autorefractors (even the open-field autorefractors) suffer from certain instrument myopia as shown in this study, where myopic shifts were reported for the objective refractions of WAM. At this point, it is interesting to mention that in the experimental subjective system showed herein, a small negative bias was also obtained (−0.034D); however, this negative bias (probably due to the closed-view environment) can be considered insignificant for practical purposes, and it is reasonable to think that accommodation in hyperopes might be controlled with such an algorithm.
With regard to the precision study, Sheppard and Davies2 evaluated the intra- and inter-test variability of the WAM-5500. Inter-test variability consisted of repeating the refraction measurements in a second session, with the corresponding realignment for each eye. We can thus establish comparisons between their inter-test variability and our intra-observer findings, since the latter was a test-retest study with realignment. We found for the M that 84.6% of the differences between two repeated measurements with realignment were within ±0.25D, slightly better results than the 73% obtained by Sheppard and Davies. However, they found a smaller mean absolute difference (−0.07±0.26D vs 0.14±0.11D), probably due to the 5 measurements they carried out within each session.
Regarding inter-observer variability, we were especially interested in analyzing the impact on the outcomes based on the clinician conducting the Subj.E procedure; however, the precision study design also allowed us to analyze the reproducibility of the WAM-5500 (i.e., inter-observer variability), which had not been done before up to our knowledge. As expected for an autorefractor,10 we did not find clinically significant differences among observers; nonetheless, worse results were obtained when comparing inter- and intra-observer variability, i.e., the mean absolute differences for the M component were of 0.015±0.177D (intra-observer) and 0.031±0.218D (inter-observer). Moreover, the percentage of cases with absolute differences below 0.25D dropped from 84.6% to 78.2% for the spherical inter-observer variability.
Finally, the precision of the experimental subjective method (Subj.E) presented herein is comparable to other methods, the mean intra-observer variability was of 0.072±0.197D for the Subj.E and 0.034±0.195D for the Subj.C. But as previously mentioned, more precise results are expected in the objective procedures (WAM) since no patient's response is needed. It is worth noting that in the case of the Subj.E, the methodology of the refraction is simplified in order to provide a method between classical subjective and objective refraction which has been shown to be clinically valid in terms of precision and agreement with the classical subjective refraction.
Even though autorefractors and wavefront refractors serve as excellent tools to assess patients’ refractive error, in this study we showed the first clinical results of a new approach to determine spherical refraction in a binocular virtual reality environment. This new approach reduces the clinician interaction during the examination, having only to press ‘Yes’/‘No’ buttons. Results showed a fairly good agreement with conventional subjective refraction and good precision, suggesting that the optical system and algorithms developed are capable of performing refraction.
This system has the potentiality to be integrated with an objective refractometer and thus provides a refractive system precise as autorefractometers and accurate as the classical subjective procedure. Further work includes the development of an algorithm for semiautomated astigmatic correction.
FundingThis research was supported by the Spanish Ministry of Economy and Competitiveness under the grants DPI2011-30090-C02-01 and MTM2012-31118, the European Union and by Davalor Salud, S.L. Carles Otero would like to thank the Generalitat de Catalunya for his awarded PhD studentship.
Conflicts of interestThe following authors hold a position that might be a potential conflict of interest related to Davalor Salud, S.L.: Jaume Pujol, position in Davalor Salud: Director of the Clinical Council of Davalor Salud. Juan Carlos Ondategui-Parra, position in Davalor Salud: Secretary of the Clinical Council of Davalor Salud.
The study was approved by the Ethics Committee of the University Hospital Mutua de Terrassa (Barcelona, Spain) and the research followed the tenets of the Declaration of Helsinki. After explaining the nature and possible consequences of the study, written informed consent was obtained from participants.