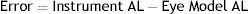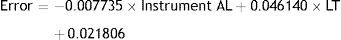To evaluate the error in the estimation of axial length (AL) with the IOLMaster partial coherence interferometry (PCI) biometer and obtain a correction factor that varies as a function of AL and crystalline lens thickness (LT).
MethodsOptical simulations were produced for theoretical eyes using Zemax-EE software. Thirty-three combinations including eleven different AL (from 20mm to 30mm in 1mm steps) and three different LT (3.6mm, 4.2mm and 4.8mm) were used. Errors were obtained comparing the AL measured for a constant equivalent refractive index of 1.3549 and for the actual combinations of indices and intra-ocular dimensions of LT and AL in each model eye.
ResultsIn the range from 20mm to 30mm AL and 3.6–4.8mm LT, the instrument measurements yielded an error between −0.043mm and +0.089mm. Regression analyses for the three LT condition were combined in order to derive a correction factor as a function of the instrument measured AL for each combination of AL and LT in the theoretical eye.
ConclusionsThe assumption of a single “average” refractive index in the estimation of AL by the IOLMaster PCI biometer only induces very small errors in a wide range of combinations of ocular dimensions. Even so, the accurate estimation of those errors may help to improve accuracy of intra-ocular lens calculations through exact ray tracing, particularly in longer eyes and eyes with thicker or thinner crystalline lenses.
Evaluar el error en la estimación de la longitud axial (LA) con el biómetro IOLMaster de interferometría de coherencia parcial (ICP), y obtener un factor de corrección que varíe en función de la LA y el grosor del cristalino (GC).
Métodos: Se realizaron simulaciones ópticas en ojos teóricos utilizando el software Zemax-EE. Se utilizaron treinta y tres combinaciones que incluían once LA diferentes (de 20 a 30mm en pasos de 1mm) y tres GC (3,6; 4,2 y 4,8mm). Se obtuvieron los errores cometidos al comparar la LA medida para un índice refractivo equivalente constante de 1,3549 y para las combinaciones reales de los índices y dimensiones intraoculares de GC y LA en cada modelo de ojo.
ResultadosEn el rango de 20 a 30mm de LA y de 3,6 a 4,8mm de EC, las mediciones instrumentales arrojaron un error comprendido entre -0,043 y +0,089mm. Se combinaron los análisis de regresión para las tres situaciones de GC con el fin de calcular un factor de corrección en función de la LA medida instrumentalmente para cada combinación de LA y GC en el ojo teórico.
ConclusionesEl supuesto de un único índice refractivo “medio” en la estimación de LA mediante el Biómetro ICP IOLMaster, causa muy pocos errores en un amplio rango de combinaciones de dimensiones oculares. Incluso así, la estimación exacta de dichos errores puede ayudar a mejorar la precisión de los cálculos de las lentes intra-oculares mediante trazado de rayos, particularmente en ojos más grandes y ojos con mayor o menor espesor del cristalino.
Accurate measurement of the axial length (AL) of the eye is critical in several research and clinical applications. Partial coherence interferometry (PCI) is a non-invasive objective method to measure axial length (AL) and is the election method for total or partial measurement of intra-ocular dimensions1,2 as a main variable for intra-ocular lens calculation. It is also used in clinical trials involving emmetropization and myopia progression3 and, recently, to evaluate the actual shape of the posterior segment of the eye.4,5 However, such biometers determine optical path lengths (OPL) and convert them into geometric/anatomical lengths by assuming estimate values for the eye internal refractive indices. In the case of the IOLMaster (Carl Zeiss Meditec, Jena, Germany), it uses a unique average index (1.3549) based on the average group refractive index of a Gullstrand's 24mm model eye for an envelope of waves at the instrument's infrared radiation wavelength λ=780nm.6
Atchison and Smith7 calculated the errors that this assumption might induce in axial length measurement during accommodation, and more recently in retinal shape estimation.8 However, no correction factor was suggested within the normal range of AL and crystalline lens thickness (LT) which might have an impact in the final estimations, as the authors acknowledge.
Beyond solely measuring AL and other biometric parameters, current intra-ocular refractive surgical procedures require a high level of accuracy in the estimation of the power of the intra-ocular lenses (IOL) to be implanted. This is particularly relevant in patients with very good preoperative visual acuity as in the case of presbyopic patients undergoing clear lens exchange (CLE) with implantation of multifocal IOL's.9 IOL power calculation has evolved from the initial empirical methods to the newest generation formulas.10 The potential errors involved in AL measurement within the normal range seem to be assumed by correction factors in the IOL formulas, but for eyes with out-of-the-normal-range internal dimensions significant errors might be involved.11,12
In the search for more accurate estimations, several authors have made significant efforts to develop new customized methods to estimate the IOL power through optical modelization13 based on the patient’ own data, obtained with the most recent methods of ocular imaging.14 As the axial length of the patient's eye is paramount in these efforts for higher accuracy, better estimations of the AL should be useful to improve the accuracy of these models.
The goal of this paper was to evaluate the impact of different combinations of AL and LT in the measurement obtained with the IOLMaster through optical ray tracing simulation, and to derive a correction method for such measurements.
MethodsOptical design programs are used to model and analyze different kinds of imaging systems including the human eye. They use Snell's law to trace the propagation of light through the surfaces of an optical system. Using ray-tracing software Zemax-EE (Zemax Development Corporation, Washington, USA) a set of unaccommodated eyes were designed based on the Navarro Eye Model.15 Three different LT values (3.6mm, 4.2mm and 4.8mm) were combined with eleven eye lengths (from 20mm to 30mm in 1.0mm steps), resulting in 33 combinations. The LT values were based on the age related changes obtained by Atchison et al.16 who pointed an average LT shift from of 3.6mm to 4.8 from 20 to 70 years of age. An additional 4.2mm intermediate value was included as a value representative of a middle-aged population from 39 to 51 years.17
Corneal thickness, curvatures and asphericities were kept constant. Anterior chamber depth (ACD) was set to vary as a function of the change in LT such that 50% of the change in LT resulted in a change in the same magnitude in the ACD. Vitreous chamber depth (VCD) was set to vary as a function of ACD and eye length as most of the axial elongation of the eye is attributed to VCD elongation.18 This was assumed for simplicity after previous simulation demonstrated no implication in the error calculations presented. As ACD and VCD have similar refractive indices, the sum of their optical path lengths (OPL) will be the approximately the same regardless of their physical length distribution. The individual group refractive indices were derived by Hitzenberger,6 starting from the known phase refractive indices at λ=550nm and assuming the dispersion of water for the ocular media.
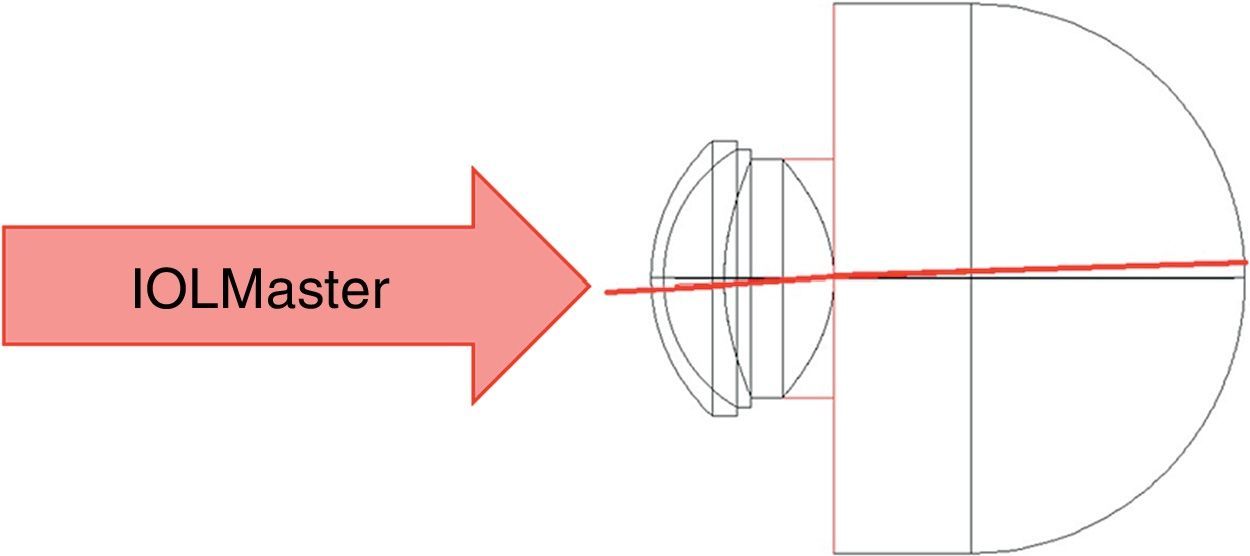
Unlike ultrasound biometry that measures AL along the optical axis of the eye, PCI – as a fixation-bound method – measures AL along the eye's visual axis. Because of the temporal displacement of the fovea in the human eye, the horizontal field angle was adjusted so that the chief ray would maintain a 5-degree angle at the 2nd nodal point (Fig. 1). Normal incidence with the first corneal surface was maintained in all theoretical simulations.
For the cornea-to-fovea physical distance to be the same between the eye model and the instrument estimated AL, the average group refractive index of the eye model must equal the one assumed by the instrument for the same wavelength. Whenever these values are different, depending mainly on varying distribution of AL and LT values, the optical measurement will result in an estimation error. The error was obtained using Eq. (1).
Here the instrument measured AL is the result of dividing the calculated OPL by the estimated group refractive index “wired in” the instrument (1.3549), and the Eye Model AL is the result of ray tracing simulation by adding each individual surface physical path length.
Linear regression was used to evaluate the error as a function of LT and AL and then combined into a single correction equation. In each step the residual error was calculated.
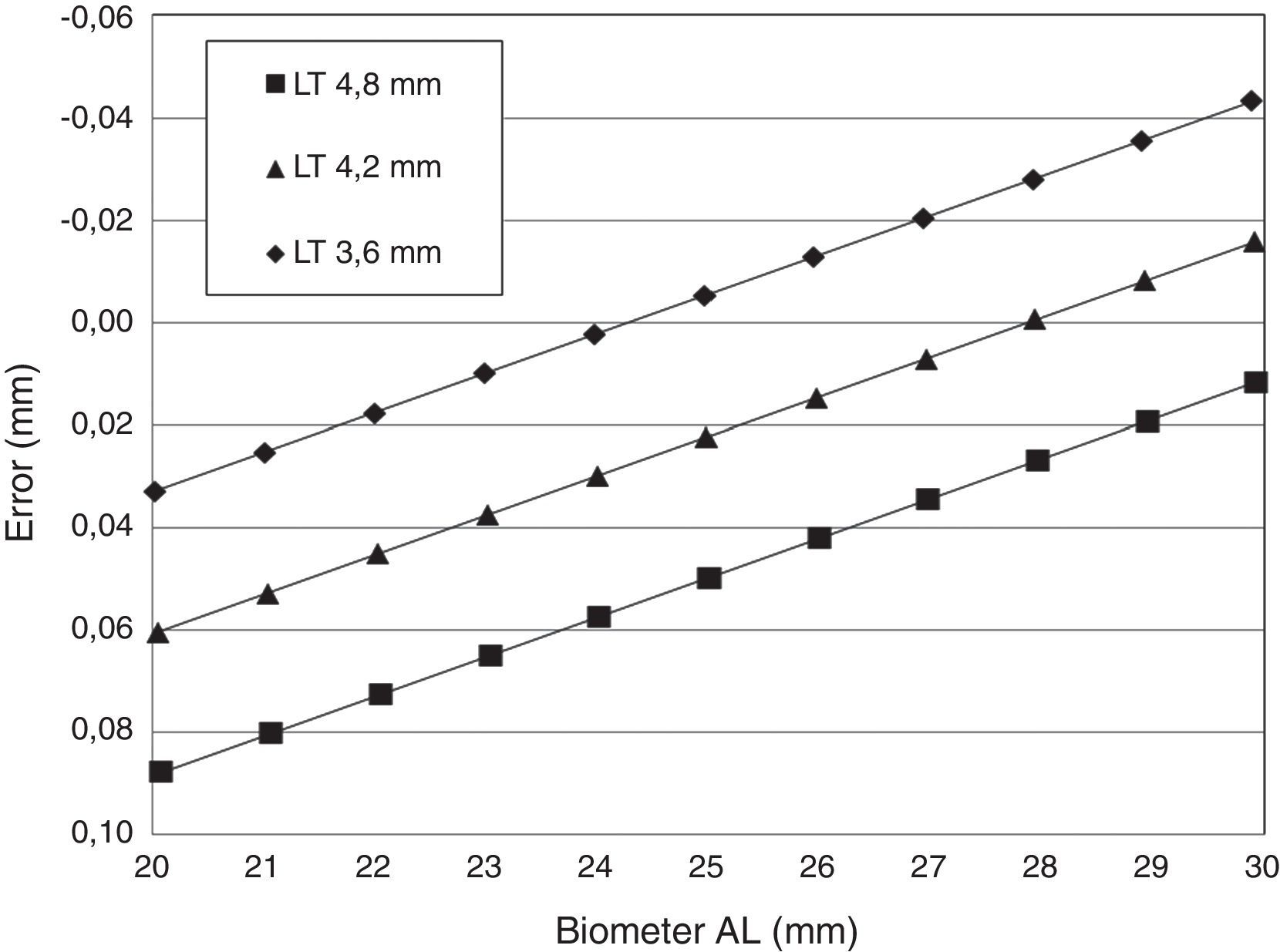
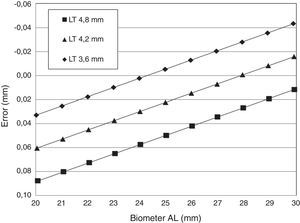
ResultsThe errors for each one of the eye models under evaluation have been calculated and plotted as a function of the axial length, for each crystalline lens thickness. Fig. 2 shows the error variations in the instrument measurements for all the 33 eye model combinations. From 20mm to 30mm axial lengths and 3.6–4.8mm lens thickness, the instrument measurements will yield an estimated error between −0.043mm and +0.089mm.
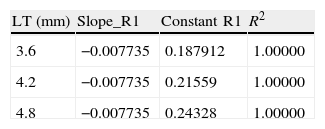
The slope obtained in the three linear regression equations was the same (−0.007735), with the equation constant values corresponding to the thinner and the thicker LT configuration presenting a difference of approximately ±0.028mm with respect to the middle thickness equation constant value (LT=4.2mm). The coefficient of determination (r2) was 1.0000 for the three equations as expected due to the linear relation between the optical path length and the real distance.
Using the parameters in Table 1, a new regression equation was derived in order to predict the variation from the constant terms in each equation for each LT. This allowed us to create a combined regression equation that will be able to estimate the amount of error as a function of AL and LT within the range of values considered in this work (Eq. (2)).
Equations Coefficients from the Regressions in Fig. 1.
| LT (mm) | Slope_R1 | Constant_R1 | R2 |
| 3.6 | −0.007735 | 0.187912 | 1.00000 |
| 4.2 | −0.007735 | 0.21559 | 1.00000 |
| 4.8 | −0.007735 | 0.24328 | 1.00000 |
Nowadays, accurate determinations of AL are of paramount importance in several research and clinical applications. From the results of the present study we can observe that the equivalent refractive index of 1.3549 used by the instrument is optimized for an AL value near 24mm with a LT around 3.6mm. This does not seem to be consistent with the normal LT value found in the general elderly population,16 especially when considering that these instruments are primarily used in pre-surgical evaluation of cataract patients. Although the errors found are quite small, usually lower than 0.1mm, which corresponds to error in the power of the IOL around 0.25 D, these errors are expected to be higher for AL values out the range than the ones plotted in Fig. 2 due to the linear relation between the error and the AL. Even so, we stress that the correction of the AL measured by the IOLMaster might not be clinical relevant when the calculation of the IOL is done using one of the traditional formulas, due to the lack of precision that they offer. On the other hand, personalized eye models can help to improve the accuracy of IOL power choice through numerical ray-tracing software like Zemax,13 but the biometric data used in the customization of the eye models must be corrected for the errors here reported, and the parameters of the IOL geometry other than the lens constant must be known. Also better estimates of group refractive indices in the infrared are needed; there is not enough information in the literature on dispersion in the various ocular media to make better estimates than the ones reported by Hitzenberger.6
Another important area that might benefit from these corrections is the clear lens exchange (CLE) surgery. In CLE, patients expect high precision results. Improving the estimation of the actual axial length will certainly improve the prediction of the most accurate post-surgical refraction.
In summary the present results demonstrates minor deviations between the AL obtained with an optical biometer and the actual value predicted using optical modelization. However, correction of AL accounting for distortions induced by refraction within the ocular media and variations in the average refractive index of the eye might help to progress further toward the desirable error-free biometric calculations in cataract surgery and CLE, particularly in longer eyes.
Conflict of interestThe authors declare that there is no conflict of interest.