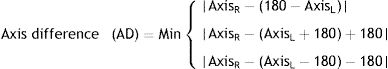To evaluate the relationship patterns between astigmatism axes of fellow eyes (rule similarity and symmetry) and to determine the prevalence of each pattern in the studied population.
MethodsThis population-based study was conducted in 2015 in Iran. All participants had tests for visual acuity, objective refraction, subjective refraction (if cooperative), and assessment of eye health at the slit-lamp. Axis symmetry was based on two different patterns: direct (equal axes) and mirror (mirror image symmetry) or enantiomorphism. Bilateral astigmatism was classified as isorule if fellow eyes had the same orientation (e.g. both eyes were with-the-rule) and as anisorule if otherwise.
ResultsOf the total cases of bilateral astigmatism, 80% were isorule, and in the studied population, the prevalence of isorule and anisorule astigmatism was 14.89% and 3.53%, respectively. The prevalence of isorule increased with age (p<0.001). The prevalence of both isorule and anisorule increased at higher degrees of spherical ametropia (p<0.001). Median inter-ocular axis difference was 10° in mirror symmetry and 20° in direct symmetry with no significant difference between two genders (p>0.288). Both symmetry patterns reduced with age (p<0.001). Among cases of bilateral astigmatism, 15.5% and 19.8% had exact direct and mirror symmetry, respectively.
ConclusionBilateral astigmatism is mainly isorule in the population and anisorule astigmatism is rare. The enantiomorphism is the most common pattern in the population of bilateral astigmatism.
Evaluar los patrones de la relación entre los ejes del astigmatismo en ojos contralaterales (similitud de la regla y simetría), y determinar la prevalencia de cada patrón en la población estudiada.
MétodosEste estudio poblacional se llevó a cabo en Irán en 2015. A todos los participantes se les realizaron pruebas de agudeza visual, refracción objetiva, refracción subjetiva (de cooperar el paciente), y valoración de la salud ocular con lámpara de hendidura. La simetría axial se basó en dos patrones diferentes: directo (ejes iguales) y especular (simetría de imagen especular) o enantiomorfismo. El astigmatismo bilateral se clasificó como directo si los ojos contralaterales tenían la misma orientación (ej.: ambos ojos estaban a favor de la regla) e inverso en caso contrario.
ResultadosDel total de casos de astigmatismo bilateral, el 80% eran a favor de la regla, y en la población estudiada la prevalencia del astigmatismo a favor de la regla y en contra de la regla fue del 14,89% y el 3,53%, respectivamente. La prevalencia del astigmatismo a favor de la regla se incrementó con la edad (p<0,001). La prevalencia del astigmatismo a favor de la regla y en contra de la regla se incrementó al aumentar los grados de ametropía esférica (p<0,001). La diferencia media del eje inter-ocular fue de 10 grados en la simetría especular y de 20 grados en la simetría directa, sin diferencia significativa entre ambos sexos (p>0,288). Ambos patrones de simetría se redujeron con la edad (p<0,001). Entre los casos de astigmatismo bilateral, en el 15,5% y el 19,8% se observaron simetría directa exacta y especular, respectivamente.
ConclusiónEn la población, el astigmatismo bilateral es principalmente a favor de la regla, siendo infrecuente el astigmatismo en contra de la regla. El enantiomorfismo es el patrón más común en la población con astigmatismo bilateral.
Refractive errors, as one of the most common vision disorders, are known as the second cause of visual impairment and low vision.1–4 Astigmatism is one of the most common types of refractive errors, and to date, there have been a multitude of reports concerning its prevalence in different age groups and geographic regions.5–7 The prevalence of astigmatism varies by age6–8 and geographic location.7,9,10 To date, prevalence rates up to 75% have been reported.11 The most common type of astigmatism orientation is with-the-rule (the axis of the minus cylinder is placed between 30° and 150°), and the most rare type is oblique astigmatism (axes between 30° and 60°).7,12 The prevalence of with-the-rule astigmatism (axes between 60° and 120°) usually decreases with age, and against-the-rule increases.13
The status of astigmatism in fellow eyes has been assessed in a number of studies.14 Certain epidemiological studies have shown that the amounts of astigmatism in fellow eyes are usually comparable, and significant anisoastigmatism is rare.14,15 In addition to study astigmatism values in fellow eyes, few studies have assessed the relationship between astigmatism axes.15–18 The first study in this regard was conducted by McKendrick and Brennan on 192 people who were mainly selected from university personnel,16 and they suggested that axis symmetry between fellow eyes is not common. Their study was not conducted on a general population and had a very small sample size. Another important study in this regard was conducted in 2008 by Guggenheim et al. on 50,996 residents of Northern England.17 Their report indicated the dominance of the mirror symmetry pattern of the astigmatism axis in fellow eyes to the direct symmetry pattern. Their study was not population-based either, and they did not provide the prevalence of different symmetry patterns.
Asharlous et al. evaluated the association of astigmatism axes in fellow eyes in 2016.19 This study presented a comprehensive analysis of the association of astigmatism axes in the fellow eyes of individuals visiting ophthalmology clinics. Although the association of the axes was well analyzed, the results may not be generalizable because the sample did not represent the general population. Therefore, the pattern of the association of bilateral astigmatism axes in the general population and the changes of these patterns with age are not clear.19
Since there is no complete description of the relationship between the astigmatism axes in fellow eyes in a population-based study, we aimed to examine this relationship in a cross-sectional population-based epidemiological study. The results of such studies and discovering hidden relationships between astigmatism axes in fellow eyes will naturally have importance in clinical terms as well as understanding the etiology of astigmatism. Information of this type can be helpful for exploring inheritance patterns and the genetic aspects of astigmatism.17,20 In the present study, we assessed the relationship between the principal meridians in fellow eyes from a different perspective compared to previous studies. We conducted a thorough analysis of the prevalence of rule similarity in bilateral astigmatism (isorule and anisorule), the prevalence of mirror and direct symmetry patterns by taking into account the different levels of symmetry, and the effect of age, gender, and spherical and cylindrical ametropia values.
MethodPopulation and samplingThis population-based cross-sectional study was conducted in underprivileged areas of Iran in 2015. The selection of study locations was based on the information provided by the Office of Rural Development of the Islamic Republic of Iran. From the list of underprivileged districts, we selected two districts for this study.
In this study, sampling was done through a multistage cluster approach. First two districts were randomly selected from the north and south of the country, and then, a number of villages were randomly selected from the list of villages in each district. Sampling from each district was proportionate to the total population according to the determined sample size. To maintain a proper balance in the sampling process, 5 villages from Kajour and 15 villages from Shahyoun were included in the study because Shahyoun villages were smaller and less populated.
In each selected household, all family members over one year old were invited to participate in the study. First a written consent was obtained from each participant. The head of the household signed the consent for persons under 18 years of age. All participants had complete examinations by two optometrists. Uncorrected visual acuity was measured in all participants. This was done with the Snellen E chart for people over 5 years and the LEA symbols chart for children under 5 years of age. Then objective refraction was done. For this purpose, first autorefraction was done using the Nidek Ref/Keratometer ARK-510A, and then these findings were verified through retinoscopy with the Heine Beta 200 retinoscope (HEINE Optotechnik, Germany). Then, subjective refraction was tested in all people, and the best-corrected visual acuity was recorded. At the conclusion of vision tests, an ophthalmologist examined the overall health of the eye, and the presence of any eye disease was recorded.
Exclusion criteria in this study included the presence of any corneal disease, including corneal ectasia (keratoconus and pellucid marginal degeneration), corneal dystrophy, any active corneal inflammation or infection, corneal scarring, history of any eye surgery affecting the cornea including cataract, refractive, and pterygium surgery, a history of ocular trauma, presence of any opacity in the ocular media such as corneal opacity and cataract which can cause erroneous refraction results, and the presence of other anterior segment diseases such as pterygium and phlyctenulosis which may involve the cornea.
DefinitionsIn this study, the results of refraction obtained by retinoscopy were used for analysis. A spherical refractive error of ≤0.50 dipoter (D) and ≥−0.50D was defined as emmetropia, more than +0.50D as hyperopia and less than −0.50D as myopia. Myopia was classified as mild, moderate, and high at ranges of −0.51 to −3.00D, −3.10 to −6.00D, and less than −6.00D, respectively. In hyperopic individuals, ranges of 0.51 to 2.00D, 2.10 to 4.00D, and more than 4.00D were considered as mild, moderate, and high hyperopia, respectively.
In this study, refraction for all subjects was recorded in minus cylinder. A minimum cylinder of 0.50D was considered in each eye. In fact, any individual who had at least 0.50D cylinder error in both eyes was entered into the analysis as a case of bilateral astigmatism. Based on the amount of astigmatism, we categorized it in three groups of mild (less than 1.00D), moderate (1.00–2.00D) and high (2.00D or more). Since the astigmatism difference between fellow eyes was small, we used the average astigmatism of left and right eyes to categorize astigmatism. We considered astigmatism with axes from 60 to 120° (90±30) as against-the-rule, from 150 to 30° (180±30) as with-the-rule, and the rest as oblique.
Rule similarityWe divided cases of bilateral astigmatism to isorule and anisorule based on the situation of the axes of astigmatism in the fellow eyes. In isorule astigmatism, the fellow eyes of an individual have similar orientations. It consists of three categories: both eyes with-the-rule (WW), both eyes against-the-rule (AA), and both eyes oblique (OO). Those with different astigmatism orientation in fellow eyes were regarded as anisorule which also has three categories: one eye with-the-rule and the other against-the-rule (WA), one eye with-the-rule and the other oblique (WO), and one eye against-the-rule and the other oblique (AO).
Symmetry patternsWe assessed the symmetry of astigmatism axes in fellow eyes under two different models: direct symmetry and mirror symmetry or enantiomorphism.17,19 In direct symmetry, the axes in fellow eyes are numerically equal, and their difference is zero. For example, the axis in the right eye is 90° and the axis of the left eye is also 90°. In mirror symmetry, however, the axes in fellow eyes are not similar, and their difference is not zero, but they are mirror images of each other. In this case, if the axes of fellow eyes are superposed, they do not cover each other, and they form a cross (for example, the left eye axis is 15° and the right eye axis is 165°, or the left eye axis is 110° and the right eye axis is 70°).
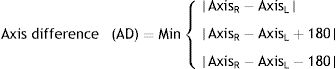
First, we examined the exact symmetry of the astigmatism axis in fellow eyes. Exact symmetry refers to a condition where there is a perfect mirror or direct symmetry. For example, a case with axes at 100° and 80° has exact mirror symmetry and a case with axes at 100° and 100° has exact direct symmetry. Therefore, two different formulas can be imagined for symmetry.19 For direct symmetry, if |AxisR−AxisL| is equal to zero, there is exact symmetry between the axes of fellow eyes. For mirror symmetry, we calculated |AxisR−(180−AxisL)|, and when the output is zero, there is exact mirror symmetry.
We did not limit this study to exact symmetry. Instead, we defined different degrees of symmetry, and we conducted a thorough assessment of the prevalence of different degrees of symmetry in the studied population.20 Suppose the axis is 20° in one eye and 162° in the other. We know that the mirror image of a 20° axis would be 160° in the fellow eye. It is true that in this example fellow eye axes are not exactly symmetrical, but they are very close to mirror symmetry. In fact, if the axis in the latter eye were 160°, we would have exact symmetry. In this example, the difference between 162 and 160 is 2°, so we can say that fellow eye axes are 2° away from exact mirror symmetry; clinically, they can be considered symmetrical. The same applies to direct symmetry, and examples would be cases with axes at 100° and 103°, 40° and 38°, or 180° and 175°.
The two |AxisR−AxisL| and |AxisR−(180−AxisL)| formulas cannot be used alone for a comprehensive and accurate assessment of mirror and direct symmetry. One factor that interferes with the analysis is the clock arithmetic nature of astigmatic axes.19 To rectify this, we used the 180 modulus. Then, we analyzed the two models to see whether the axes of fellow eyes were closer to mirror symmetry or direct symmetry. We calculated the deviation of the inter-ocular axis difference (AD) from exact symmetry in these two models.19 The first model was the direct symmetry model defined as:
And for the mirror symmetry model, we used:
In each of these models, three calculations are done for each pair of eyes, and the smallest value is considered as the absolute deviation from mirror or direct symmetry. First, we examine direct symmetry with an example. For a given axis of 180° in the right eye and 4° in the left eye, the deviation from exact direct symmetry is only 4°, but if we use |AxisR−AxisL|, the difference would be 176°. This error arises from the clock arithmetic nature in astigmatic axes. The same problem may exist for other situations. The problem can be resolved by applying the 180 modulus to the model, i.e. once adding 180 to the output of the formula and once subtracting it from 180. Eventually, the smallest absolute value generated from these three formulas is considered as the deviation from exact symmetry. In the example with axes at 180° and 4° in fellow eyes, results with direct symmetry formulas are 176°, 356°, and 4°, respectively, and 4° was considered as the deviation from exact direct symmetry for the fellow eyes. The same process was followed with the mirror symmetry model to calculate the axis difference between fellow eyes, and we considered the deviation from exact symmetry as the inter-ocular difference.
Based on these analyses, the symmetry of the axes in fellow eyes would be closer to the model producing a smaller value. Higher values would indicate further deviation from exact symmetry. With this method, we can find whether the axes in fellow eyes tend more toward mirror symmetry or direct symmetry. Since the data in this study and similar studies do not follow normal distribution and there is too much skewness, we used the median of the data as the central tendency index. We compared the median of inter-ocular differences to determine whether the axes of fellow eyes tended more toward mirror symmetry or direct symmetry. Naturally, it can be assumed that the dominant pattern tends toward the model that generates a lower median. For example, if the median difference with the direct and mirror symmetry models is 5° and 15°, respectively, it means there is a tendency toward direct symmetry more than mirror symmetry.
We determined the absolute frequency percentages in both models. The inter-ocular difference in axis was classified into five categories: zero degrees difference (exact symmetry), 0° to 5°, 6° to 10°, 11° to 15°, and more than 15° difference.19 We calculated the absolute and cumulative frequencies in the studied sample in each of these five categories. For example, for the mirror symmetry model, we determined the percentage of individuals who had exact symmetry, as well as the percentage of people who had less than 5° deviation from exact mirror symmetry (e.g. axes at 10° and 172°), etc.
Statistical analysesIn the first part of the analysis, we studied the overall prevalence of bilateral astigmatism as well as isorule and anisorule types in the total sample and different sub-groups, and we examined the trend of prevalence changes based on demographics and different refractive statuses. The analysis of symmetry patterns consisted of two main processes. First, we compared the median of the inter-ocular difference in astigmatism axis in both the direct and mirror models in all sub-groups of the study, including gender, age groups, and different levels of spherical ammetropia, etc. using the Wilcoxon test. Then we used simple and multiple regression analyses to explore changes in both symmetry patterns in relation to independent variables such as gender, age, etc.
ResultsSelected samples were 3851 people, and 3314 (response rate: 86.5%) participated in the study. After applying the exclusion criteria, data from 3246 was used in the analyses. Mean age of the participants was 37.3±21.2 years (2–93 years), and 56.5% (1834) of them were female.
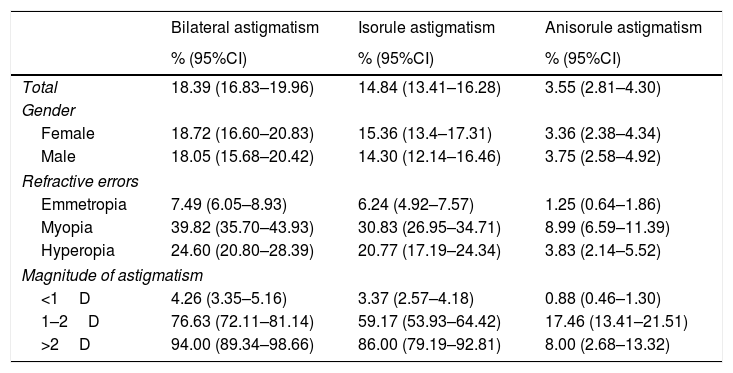
Analysis showed that 18.42% of the participants of this study had at least 0.50 D of astigmatism in both eyes. Table 1 presents the prevalence of bilateral astigmatism of more than 0.50 D by gender, location of residence, and spherical refractive error. The prevalence of isorule and anisorule astigmatism was 14.89% (80% of all cases with bilateral astigmatism) and 3.53%, respectively.
The prevalence of bilateral, isorule, and anisorule astigmatism by gender, refractive errors and magnitude of astigmatism.
| Bilateral astigmatism | Isorule astigmatism | Anisorule astigmatism | |
|---|---|---|---|
| % (95%CI) | % (95%CI) | % (95%CI) | |
| Total | 18.39 (16.83–19.96) | 14.84 (13.41–16.28) | 3.55 (2.81–4.30) |
| Gender | |||
| Female | 18.72 (16.60–20.83) | 15.36 (13.4–17.31) | 3.36 (2.38–4.34) |
| Male | 18.05 (15.68–20.42) | 14.30 (12.14–16.46) | 3.75 (2.58–4.92) |
| Refractive errors | |||
| Emmetropia | 7.49 (6.05–8.93) | 6.24 (4.92–7.57) | 1.25 (0.64–1.86) |
| Myopia | 39.82 (35.70–43.93) | 30.83 (26.95–34.71) | 8.99 (6.59–11.39) |
| Hyperopia | 24.60 (20.80–28.39) | 20.77 (17.19–24.34) | 3.83 (2.14–5.52) |
| Magnitude of astigmatism | |||
| <1D | 4.26 (3.35–5.16) | 3.37 (2.57–4.18) | 0.88 (0.46–1.30) |
| 1–2D | 76.63 (72.11–81.14) | 59.17 (53.93–64.42) | 17.46 (13.41–21.51) |
| >2D | 94.00 (89.34–98.66) | 86.00 (79.19–92.81) | 8.00 (2.68–13.32) |
CI: confidence interval.
D: diopter.
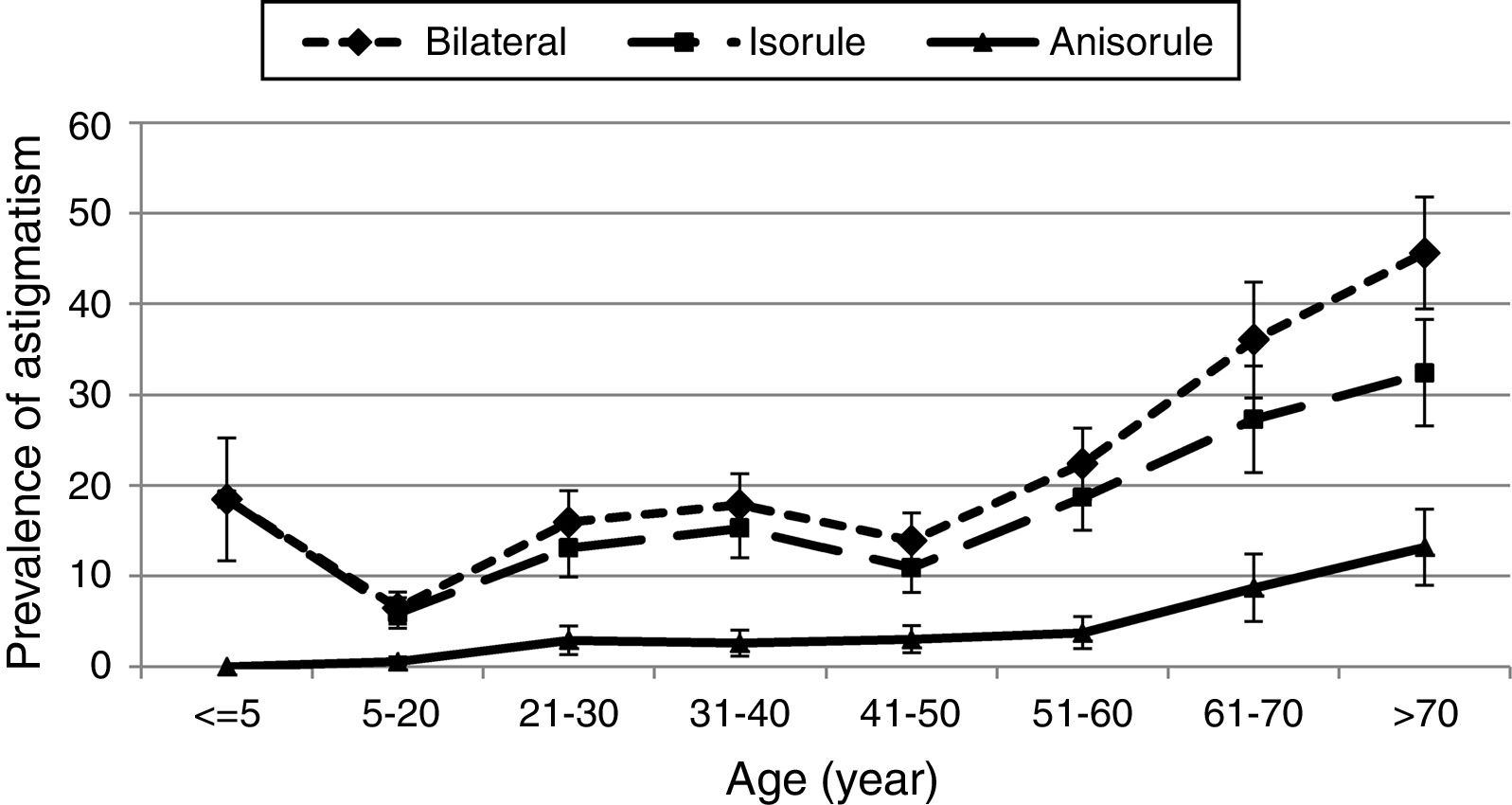
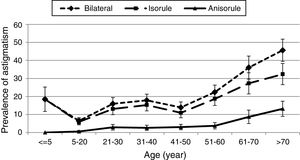
There were no significant inter-gender differences in the prevalence rates of isorule astigmatism (p=0.479) and anisorule astigmatism (p=0.617). Fig. 1 presents the prevalence of different types of bilateral astigmatism according to age.
As displayed in Fig. 1, isorule astigmatism in the under-five-year age group was 18.48%. The prevalence decreased in the 6 to 20-year age group and then took an upward trend such that the highest prevalence of isorule astigmatism was observed in the over-70-year age group. In people over 5 years of age, the prevalence of isorule astigmatism significantly increased with age (p<0.001).
However, the prevalence of anisorule astigmatism increased linearly from the under-five to the over-70 age groups and there was no case of anisorule astigmatism in the under-5-year age group, while the rate was 13.19% for the over-70-year age group (p<0.001).
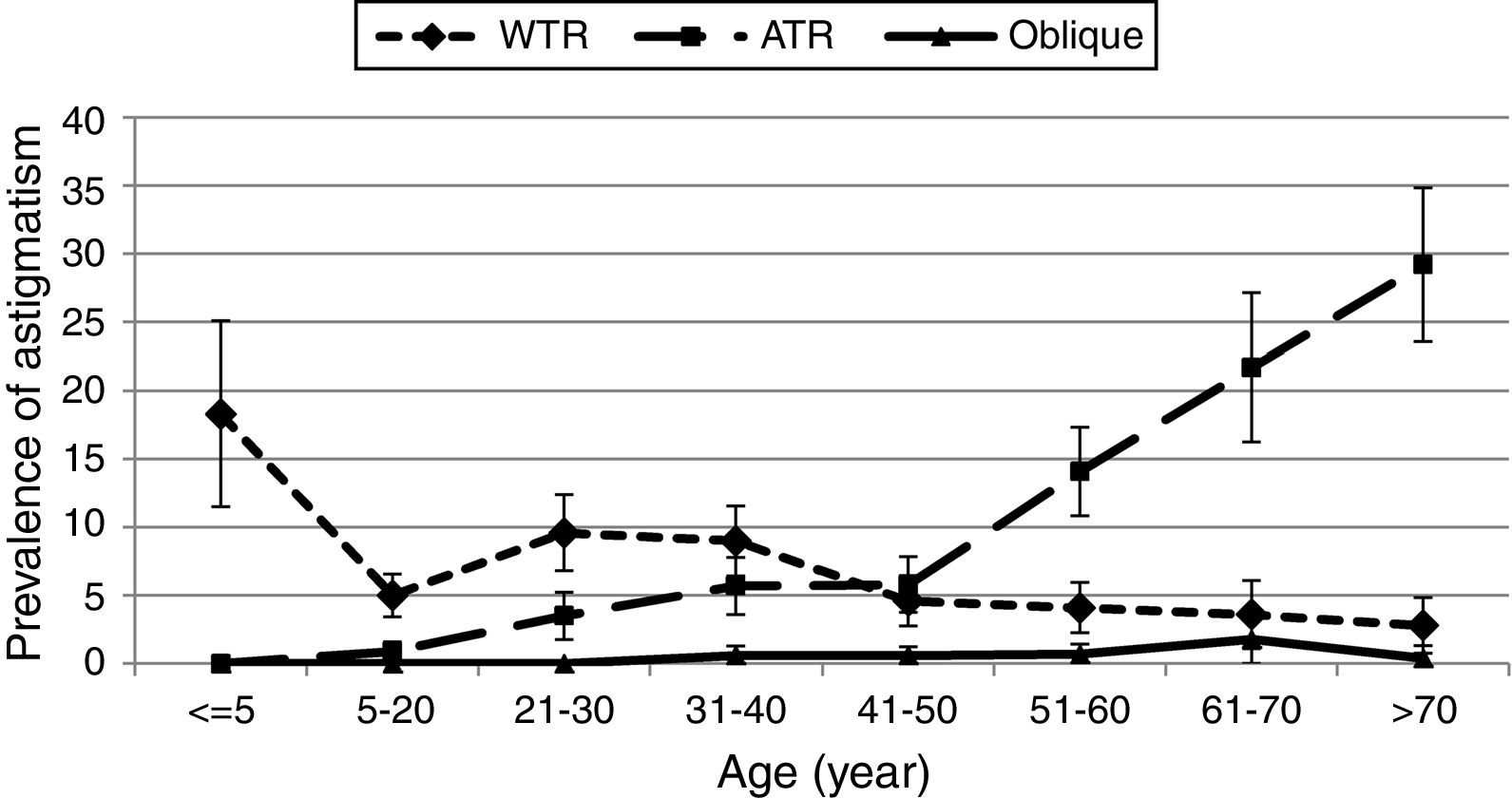
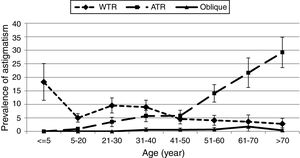
The prevalence of WA, WO, and AO in this study was 0.63%, 0.55%, and 0.76%, respectively. Our findings also showed that the prevalence of isorule with-the-rule astigmatism, isorule against-the-rule astigmatism, and isorule oblique astigmatism was 6.26%, 8.16%, and 0.42%, respectively. Overall, cases of isorule astigmatism, 42.2% were with-the-rule, 55% were against-the-rule, and 2.8% were oblique. Fig. 2 shows the prevalence of different types of isorule astigmatism according to age. Accordingly, the prevalence of WTR isorule astigmatism decreased and the prevalence of ATR isorule astigmatism increased by age.
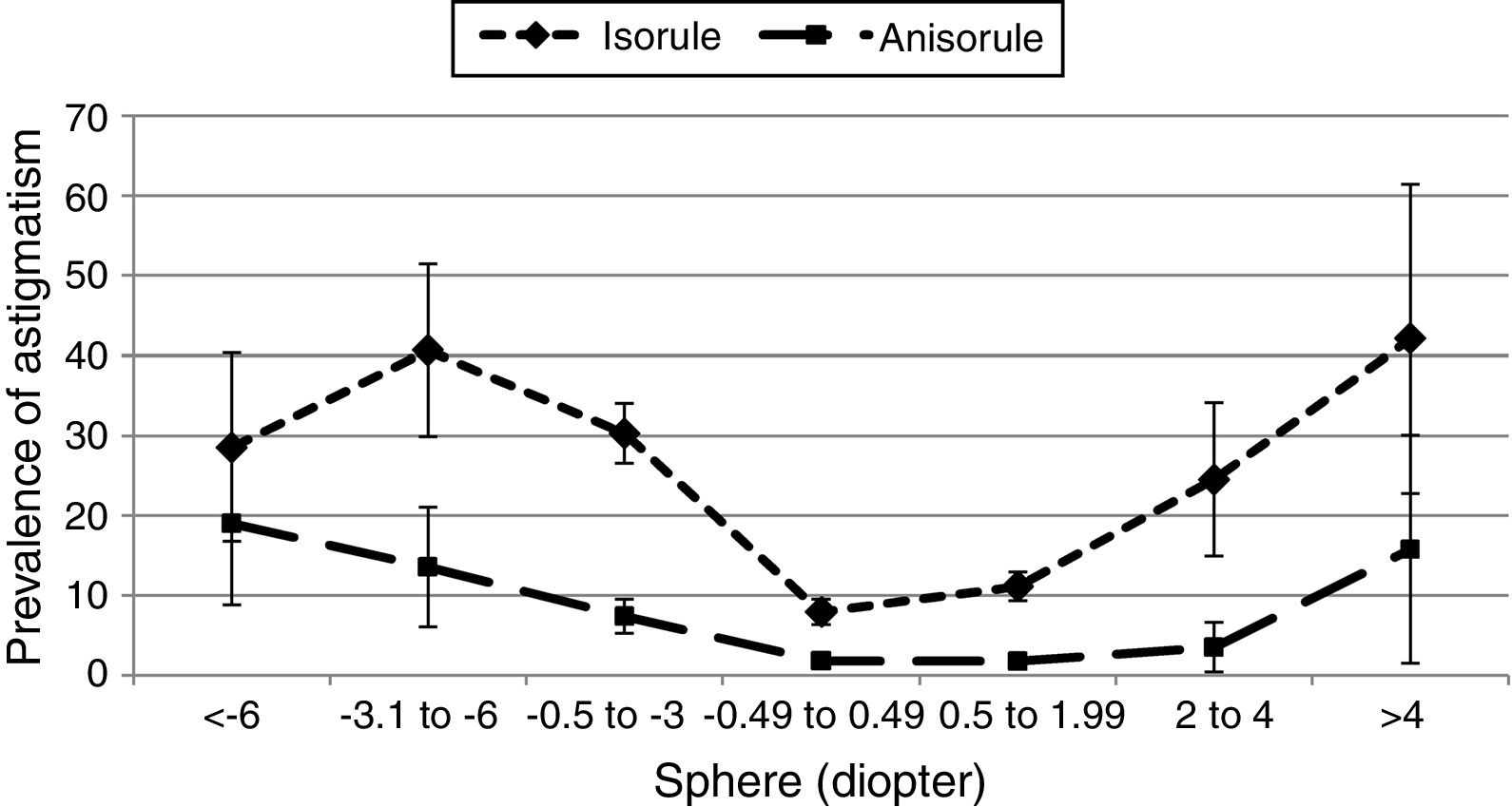
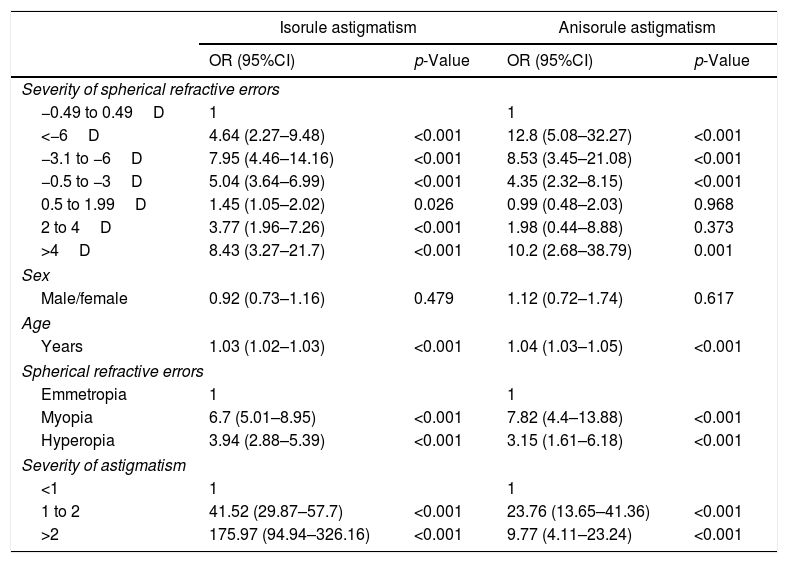
As demonstrated in Table 1, the highest prevalence of isorule astigmatism was observed in cases of astigmatism greater than 2.00D, and the prevalence of isorule astigmatism significantly increased at higher degrees of astigmatism (Table 2), while the highest prevalence of anisorule astigmatism was observed in cases with 1.00 to 2.00D of astigmatism.
The association between isorule and anisorule astigmatism according studies variables.
| Isorule astigmatism | Anisorule astigmatism | |||
|---|---|---|---|---|
| OR (95%CI) | p-Value | OR (95%CI) | p-Value | |
| Severity of spherical refractive errors | ||||
| −0.49 to 0.49D | 1 | 1 | ||
| <−6D | 4.64 (2.27–9.48) | <0.001 | 12.8 (5.08–32.27) | <0.001 |
| −3.1 to −6D | 7.95 (4.46–14.16) | <0.001 | 8.53 (3.45–21.08) | <0.001 |
| −0.5 to −3D | 5.04 (3.64–6.99) | <0.001 | 4.35 (2.32–8.15) | <0.001 |
| 0.5 to 1.99D | 1.45 (1.05–2.02) | 0.026 | 0.99 (0.48–2.03) | 0.968 |
| 2 to 4D | 3.77 (1.96–7.26) | <0.001 | 1.98 (0.44–8.88) | 0.373 |
| >4D | 8.43 (3.27–21.7) | <0.001 | 10.2 (2.68–38.79) | 0.001 |
| Sex | ||||
| Male/female | 0.92 (0.73–1.16) | 0.479 | 1.12 (0.72–1.74) | 0.617 |
| Age | ||||
| Years | 1.03 (1.02–1.03) | <0.001 | 1.04 (1.03–1.05) | <0.001 |
| Spherical refractive errors | ||||
| Emmetropia | 1 | 1 | ||
| Myopia | 6.7 (5.01–8.95) | <0.001 | 7.82 (4.4–13.88) | <0.001 |
| Hyperopia | 3.94 (2.88–5.39) | <0.001 | 3.15 (1.61–6.18) | <0.001 |
| Severity of astigmatism | ||||
| <1 | 1 | 1 | ||
| 1 to 2 | 41.52 (29.87–57.7) | <0.001 | 23.76 (13.65–41.36) | <0.001 |
| >2 | 175.97 (94.94–326.16) | <0.001 | 9.77 (4.11–23.24) | <0.001 |
D: diopter.
CI: confidence interval.
OR: odds ratio.
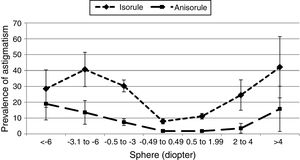
The trend of changes in the prevalence of isorule and anisorule astigmatism in relation to the degree of spherical ametropia is shown in Fig. 3. As illustrated, the prevalence of both isorule and anisorule types of astigmatism increased at higher degrees of spherical refractive error, albeit, the upward trend was steeper for isorule astigmatism. Results of logistic regression tests regarding the relation between the degree of spherical refractive error and the prevalence of isorule and anisorule astigmatism are presented in Table 2.
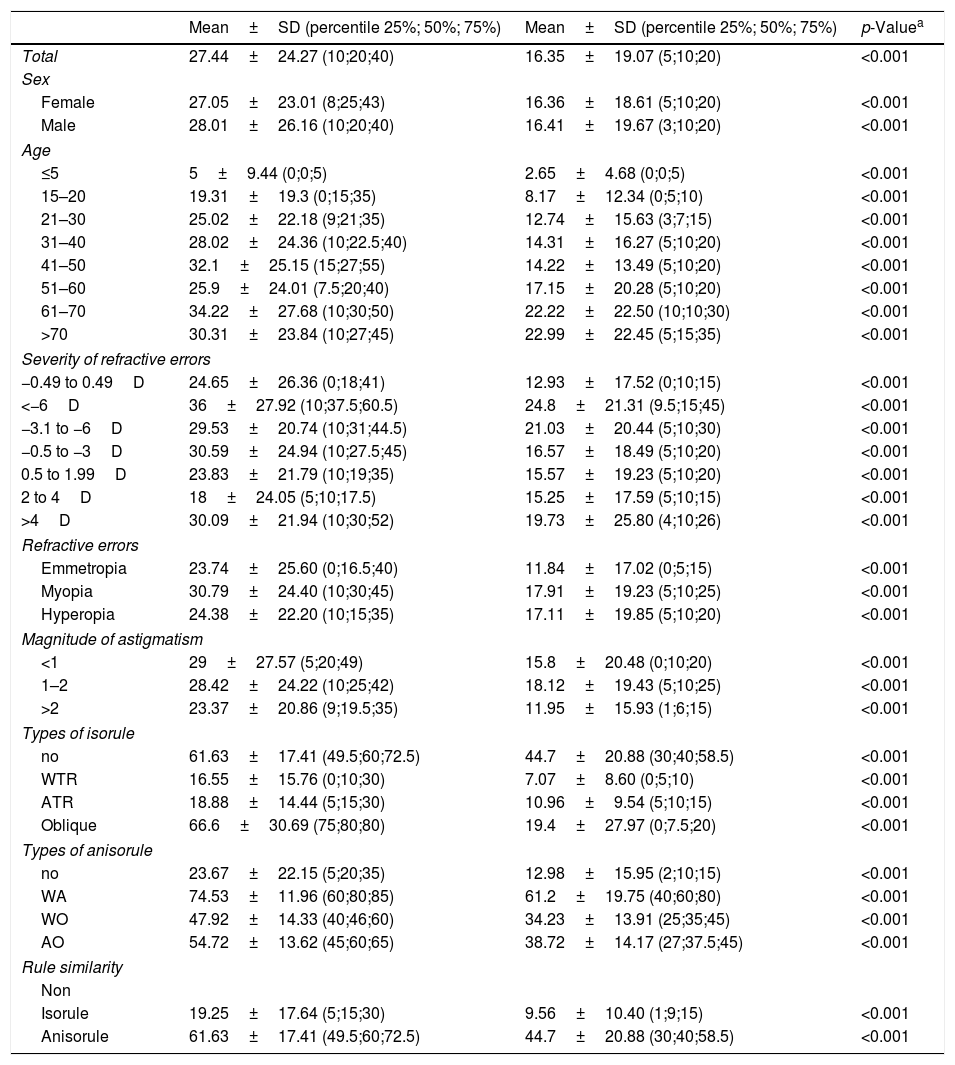
Results of the analyses on direct and mirror symmetry models are shown in Table 3. The absolute median inter-ocular differences in astigmatism axis were calculated for both models. Calculations showed an overall difference of 10 for the mirror symmetry model and 20 for the direct symmetry model. The median for the mirror symmetry model was significantly less than that of the direct symmetry model. The difference observed between the medians in these two models was statistically significant in all studied subgroups. The results of the Wilcoxon test in all subgroups are summarized in Table 3.
Descriptive statistics of absolute difference in the axis of astigmatism between fellow eyes under the mirror and direct symmetry models.
| Mean±SD (percentile 25%; 50%; 75%) | Mean±SD (percentile 25%; 50%; 75%) | p-Valuea | |
|---|---|---|---|
| Total | 27.44±24.27 (10;20;40) | 16.35±19.07 (5;10;20) | <0.001 |
| Sex | |||
| Female | 27.05±23.01 (8;25;43) | 16.36±18.61 (5;10;20) | <0.001 |
| Male | 28.01±26.16 (10;20;40) | 16.41±19.67 (3;10;20) | <0.001 |
| Age | |||
| ≤5 | 5±9.44 (0;0;5) | 2.65±4.68 (0;0;5) | <0.001 |
| 15–20 | 19.31±19.3 (0;15;35) | 8.17±12.34 (0;5;10) | <0.001 |
| 21–30 | 25.02±22.18 (9;21;35) | 12.74±15.63 (3;7;15) | <0.001 |
| 31–40 | 28.02±24.36 (10;22.5;40) | 14.31±16.27 (5;10;20) | <0.001 |
| 41–50 | 32.1±25.15 (15;27;55) | 14.22±13.49 (5;10;20) | <0.001 |
| 51–60 | 25.9±24.01 (7.5;20;40) | 17.15±20.28 (5;10;20) | <0.001 |
| 61–70 | 34.22±27.68 (10;30;50) | 22.22±22.50 (10;10;30) | <0.001 |
| >70 | 30.31±23.84 (10;27;45) | 22.99±22.45 (5;15;35) | <0.001 |
| Severity of refractive errors | |||
| −0.49 to 0.49D | 24.65±26.36 (0;18;41) | 12.93±17.52 (0;10;15) | <0.001 |
| <−6D | 36±27.92 (10;37.5;60.5) | 24.8±21.31 (9.5;15;45) | <0.001 |
| −3.1 to −6D | 29.53±20.74 (10;31;44.5) | 21.03±20.44 (5;10;30) | <0.001 |
| −0.5 to −3D | 30.59±24.94 (10;27.5;45) | 16.57±18.49 (5;10;20) | <0.001 |
| 0.5 to 1.99D | 23.83±21.79 (10;19;35) | 15.57±19.23 (5;10;20) | <0.001 |
| 2 to 4D | 18±24.05 (5;10;17.5) | 15.25±17.59 (5;10;15) | <0.001 |
| >4D | 30.09±21.94 (10;30;52) | 19.73±25.80 (4;10;26) | <0.001 |
| Refractive errors | |||
| Emmetropia | 23.74±25.60 (0;16.5;40) | 11.84±17.02 (0;5;15) | <0.001 |
| Myopia | 30.79±24.40 (10;30;45) | 17.91±19.23 (5;10;25) | <0.001 |
| Hyperopia | 24.38±22.20 (10;15;35) | 17.11±19.85 (5;10;20) | <0.001 |
| Magnitude of astigmatism | |||
| <1 | 29±27.57 (5;20;49) | 15.8±20.48 (0;10;20) | <0.001 |
| 1–2 | 28.42±24.22 (10;25;42) | 18.12±19.43 (5;10;25) | <0.001 |
| >2 | 23.37±20.86 (9;19.5;35) | 11.95±15.93 (1;6;15) | <0.001 |
| Types of isorule | |||
| no | 61.63±17.41 (49.5;60;72.5) | 44.7±20.88 (30;40;58.5) | <0.001 |
| WTR | 16.55±15.76 (0;10;30) | 7.07±8.60 (0;5;10) | <0.001 |
| ATR | 18.88±14.44 (5;15;30) | 10.96±9.54 (5;10;15) | <0.001 |
| Oblique | 66.6±30.69 (75;80;80) | 19.4±27.97 (0;7.5;20) | <0.001 |
| Types of anisorule | |||
| no | 23.67±22.15 (5;20;35) | 12.98±15.95 (2;10;15) | <0.001 |
| WA | 74.53±11.96 (60;80;85) | 61.2±19.75 (40;60;80) | <0.001 |
| WO | 47.92±14.33 (40;46;60) | 34.23±13.91 (25;35;45) | <0.001 |
| AO | 54.72±13.62 (45;60;65) | 38.72±14.17 (27;37.5;45) | <0.001 |
| Rule similarity | |||
| Non | |||
| Isorule | 19.25±17.64 (5;15;30) | 9.56±10.40 (1;9;15) | <0.001 |
| Anisorule | 61.63±17.41 (49.5;60;72.5) | 44.7±20.88 (30;40;58.5) | <0.001 |
SD: standard deviation; D: diopter; WTR: with-the-rule; ATR: against-the-rule; W: WTR; A: ATR; O: oblique.
Based on our findings, there was no significant inter-gender difference in the mirror symmetry model (p=0.644) or the direct symmetry model (p=0.288). We also examined the median with both models in different age groups. Results of this analysis showed that the under five-year-old age group has the lowest inter-ocular difference with both models. The median of this difference increased from this age up to before presbyopia, such that after the age of presbyopia, the inter-ocular difference in astigmatism axis was higher than before the age of presbyopia with both models.
We also examined the median inter-ocular difference at different levels of spherical refraction error. No significant differences were observed between the different groups of spherical ametropia with the mirror symmetry models (p=0.375). But with the direct symmetry model, the median inter-ocular difference in astigmatism axis significantly varied by the degree of refractive error (p<0.001) such that the highest median was observed in cases with a spherical error worse than −6.00D and the lowest median in cases with spherical worse than +4.00D.
We examined the symmetry situation in the two isorule and anisorule groups as well. The median inter-ocular difference in astigmatism axis was much lower in the isorule group than the anisorule group with both direct and mirror symmetry models (p<0.001). Analysis in isorule sub-groups showed that cases of WW had the lowest inter-ocular difference. The medians were not significantly different among the three isorule groups of WW, AA, and OO with the mirror model; however, while the medians with the direct symmetry model were comparatively low in the two WW and AA sub-groups, it was much higher in the OO sub-group. A similar analysis was performed for anisorule subgroups. With both symmetry models, the lowest and highest median inter-ocular differences were observed in the WO and WA sub-groups.
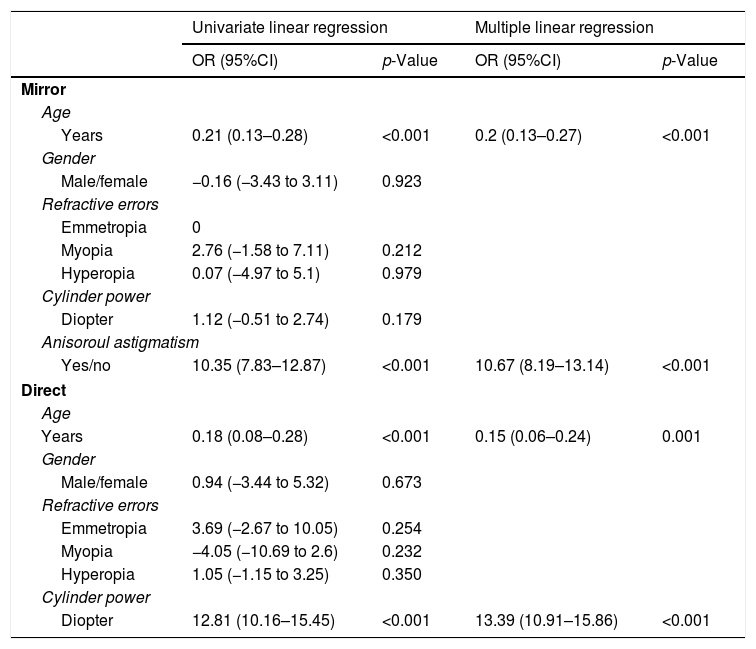
Finally, the relationship of mirror and direct models with select variables were examined in simple and multiple regression models. Results of these models are summarized in Table 4. As demonstrated, both the mirror and direct models showed statistically significant relations with age and anisorule astigmatism.
Univariate linear regression and multiple linear regression analysis of the associations between symmetry in mirror and direct patterns and some factors.
| Univariate linear regression | Multiple linear regression | |||
|---|---|---|---|---|
| OR (95%CI) | p-Value | OR (95%CI) | p-Value | |
| Mirror | ||||
| Age | ||||
| Years | 0.21 (0.13–0.28) | <0.001 | 0.2 (0.13–0.27) | <0.001 |
| Gender | ||||
| Male/female | −0.16 (−3.43 to 3.11) | 0.923 | ||
| Refractive errors | ||||
| Emmetropia | 0 | |||
| Myopia | 2.76 (−1.58 to 7.11) | 0.212 | ||
| Hyperopia | 0.07 (−4.97 to 5.1) | 0.979 | ||
| Cylinder power | ||||
| Diopter | 1.12 (−0.51 to 2.74) | 0.179 | ||
| Anisoroul astigmatism | ||||
| Yes/no | 10.35 (7.83–12.87) | <0.001 | 10.67 (8.19–13.14) | <0.001 |
| Direct | ||||
| Age | ||||
| Years | 0.18 (0.08–0.28) | <0.001 | 0.15 (0.06–0.24) | 0.001 |
| Gender | ||||
| Male/female | 0.94 (−3.44 to 5.32) | 0.673 | ||
| Refractive errors | ||||
| Emmetropia | 3.69 (−2.67 to 10.05) | 0.254 | ||
| Myopia | −4.05 (−10.69 to 2.6) | 0.232 | ||
| Hyperopia | 1.05 (−1.15 to 3.25) | 0.350 | ||
| Cylinder power | ||||
| Diopter | 12.81 (10.16–15.45) | <0.001 | 13.39 (10.91–15.86) | <0.001 |
CI: confidence interval.
OR: odds ratio.
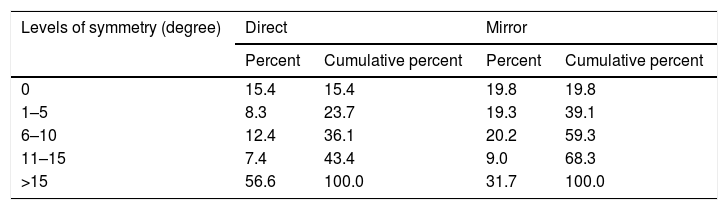
In addition to comparing the overall dominance of the two direct and mirror symmetry models, we assessed the prevalence of different degrees of fellow eye axis symmetry in the studied sample. Results of this analysis are summarized in Table 5. Direct and mirror symmetry was observed in 15.4% and 19.8%, respectively. Under the direct and mirror models, 43.4% and 68.3% of the cases were within 15° deviation from exact symmetry.
Absolute and cumulative frequencies of different levels of symmetry under the direct and mirror models.
| Levels of symmetry (degree) | Direct | Mirror | ||
|---|---|---|---|---|
| Percent | Cumulative percent | Percent | Cumulative percent | |
| 0 | 15.4 | 15.4 | 19.8 | 19.8 |
| 1–5 | 8.3 | 23.7 | 19.3 | 39.1 |
| 6–10 | 12.4 | 36.1 | 20.2 | 59.3 |
| 11–15 | 7.4 | 43.4 | 9.0 | 68.3 |
| >15 | 56.6 | 100.0 | 31.7 | 100.0 |
This is the first comprehensive population-based study on the relationship and symmetry of astigmatism axis in fellow eyes. In this study, we tried to perform a full analysis of the symmetry of axes in fellow eyes in the overall population. To date, only a handful of studies were conducted on this topic, and this study is quite unique for several reasons such as being population based, examining rule similarity as a novel approach, applying proper calculation methods and statistical analyses to examine symmetry models, as well as determining the prevalence of various symmetry degrees in the population.
According to the findings of this study, the majority of cases of bilateral astigmatism are isorule astigmatism, and anisorule astigmatism is rare in the general population. Therefore, when we encounter patients with anisorule astigmatism with a large inter-ocular difference (for example, axes of 85° and 150° in the right and left eyes), we should consider the possibility of a number of acquired corneal disorders that can affect astigmatism. For example, the presence of unilateral corneal scarring,21,22 pterygium23,24 and even keratoconus25,26 may interfere with the isorule pattern in astigmatism. Therefore, based on the results of this study and clinical experience, we can say that cases of anisorule astigmatism need to be examined to ensure corneal health and rule out possible disease conditions.
As can be deduced from the results, gender is not a determinant of the prevalence of rule similarity, and the distribution of rule similarity is comparable in both genders in the population. Based on the findings in the studied age groups, rule similarity increases in the population with age, such that it is more than 30% after the age of 70 years. One reason for the high prevalence of isorule astigmatism after presbyopia onset can be the high prevalence of astigmatism at this age. The results of this study showed a higher prevalence of astigmatism in older age, especially after 40. In agreement with our study, most previous studies have shown steady prevalence trends for astigmatism during adolescence and adulthood, but the prevalence increases after the age of onset of presbyopia.27–31 Therefore, the high prevalence of isorule in the elderly population can be attributed to the high prevalence of astigmatism, because the pattern of increase in isorule in the studied population was similar to the pattern of increase in the overall prevalence of astigmatism. The age-related changes in different types of isorule astigmatism, including WW, AA, and OO, were similar to the findings of previous studies, such that with-the-rule astigmatism had a decreasing trend, against-the-rule astigmatism had an increasing trend, and oblique astigmatism had a relatively steady trend.14,27,32,33 Since this is not a new finding and is addressed in most previous studies, we found no need to discuss it further.
The prevalence of isorule astigmatism increased at higher levels of spherical refractive error. As can be seen in the results, the lowest rate of anisorule astigmatism is in emmetropic and low hyperopic individuals. At higher levels of ametropia, whether hyperopia or myopia, isorule astigmatism increases in prevalence. The same trend applies to the anisorule type, albeit with a much less steep slope. As can be observed in the results, the overall prevalence of astigmatism in myopia and hyperopia is higher than in emmetropia. In fact, the prevalence of astigmatism increases as the degree of spherical ametropia increases. Given that there is an increasing trend for both isorule and anisorule types, the most important reason for this increase is the high prevalence of astigmatism is high ametropia. The findings of previous studies regarding the relationship between astigmatism prevalence and spherical ametropia is in agreement with the results of this study, and most studies confirm the increasing prevalence of astigmatism with age.34–36 According to results, the median absolute inter-ocular difference between the astigmatism axis in fellow eyes was smaller with the mirror symmetry model than with the direct symmetry model. In other words, there was less deviation from exact symmetry in mirror symmetry than direct symmetry, which indicates that the axes in fellow eyes in the population tend toward mirror symmetry more than direct symmetry. This is consistent with the findings discussed by Guggenheim et al. who investigated the relationship between fellow eye axes.17 McKendrick and Brennan were the first to study axis symmetry in fellow eyes in 1997.16 Their results suggested that fellow-eye symmetry is not a common finding. The findings of their study are not reliable for two reasons. First, the sample size was very small and limited to 192 people, and they were not selected from the general population. Secondly, the symmetry analysis was not an accurate method; the clock arithmetic nature of the axes in fellow eyes was overlooked and the 180 modulus was not used in symmetry calculation models. For these reasons, the results of the present study are far more reliable than their results.
Analysis of symmetry data in different age groups showed that the principal meridians in fellow eyes were most symmetric in under-5-year olds. In fact, in these ages, fellow eye astigmatism axes have the most symmetry. Symmetry reduces with age, but the reduction is not uniform. Of note, is that direct symmetry changes with age more than mirror symmetry. Overall, this study shows better symmetry before the age of presbyopia onset compared to after 40–50 years, particularly with direct symmetry. Based on these findings, we could say that astigmatism has an innate tendency to have similar axes in fellow eyes, because there is better symmetry in children. Previous studies have also pointed to the symmetrical nature of astigmatism in fellow eyes.20 But with aging, a variety of environmental factors14 such as the position and pressure of the eyelids,37–39 pressure from extraocular muscles,40,41 nutrition,42 etc. cause changes in astigmatism and the deviation of its axes from exact symmetry toward asymmetry. One possible reason to explain the greater asymmetry after the age of presbyopia can be cylindrical changes caused by different types of cataracts, even at mild degrees.42 According to Pesudovs and Elliott, cataract, especially the cortical type, can create significant changes up to 0.75D in astigmatism.43
Analysis in the three subgroups of isorule astigmatism showed best symmetry in WW eyes in both mirror and direct symmetry. In other words, we can say that people who have bilateral with-the-rule astigmatism have the most mirror and direct symmetry. It should be noted that the status of mirror symmetry in all three types of isorule symmetry was almost identical. In cases with direct symmetry, AA and WW subgroups showed good symmetry, while there was much less symmetry in OO isorule astigmatism. In other words, people who have bilateral oblique astigmatism tend toward mirror symmetry, and direct symmetry is observed much less frequently. Similar results were found in Guggenheim's study17 and there is no significant difference between the two studies in this regard. From this, we could conclude that bilateral oblique astigmatism with direct symmetry is the rarest isorule astigmatism in the population (e.g. axis of 40 in both eyes).
One of the valuable aspects examined in this study was the prevalence of different degrees of symmetry in the population. As can be seen in the results, less than one-fifth of fellow eyes with bilateral astigmatism have exact symmetry, among these, the prevalence of exact mirror symmetry is higher than the direct type. Since limiting data to exact symmetry only would cause much loss of data, we also studied various degrees of symmetry among all cases of bilateral astigmatism. For example, although axes at 10° and 172° in the left and right eyes do not have exact mirror symmetry (10° and 170°), they can be considered to have relative symmetry. Assessments in this study indicated that about half of cases of bilateral astigmatism are within 15° of exact direct symmetry, and about 70% of them are within 15° of exact mirror symmetry. These findings show that the principal meridians in fellow eyes tend to be symmetric. These findings can be used in studies of astigmatism heredity and genetics. Previous studies have also pointed out that astigmatism is a symmetrical hereditary bilateral disorder.14,20,44
Symmetry and being isorule is important in the clinical management and prescribing glasses to cases of astigmatism as well. Given their meridional magnification effect, cylindrical glasses can cause spatial distortions and consequently asthenopia and headaches for patients.45 Such spatial distortions become more disturbing when the axes in fellow eyes deviate from the 180 and 90 symmetric position and in fact become anisorule and asymmetric.46 These problems worsen under binocular vision, and involve the binocular spatial perception.46 To reduce or prevent such potential problems, previous studies have suggested that the axes on the prescription be as close to 180 and 90 symmetry as possible, albeit without compromising visual acuity.30,47 The findings of this study indicate that most cases of astigmatism tend toward symmetry, and fortunately, most bilateral cases are isorule with-the-rule and against-the-rule, and spatial problems and binocular stereoscopic perceptions may be a problem only for a small percentage of patients.
ConclusionSimilar to the results of a previous clinical-based study, we found that the majority of cases of bilateral astigmatism in the population are isorule. Gender is not a determinant in the prevalence of isorule astigmatism, while age is associated with significant changes in its prevalence. Overall, the prevalence of isorule and anisorule astigmatism increases with age in the population, with the slope being much steeper in isorule astigmatism. The prevalence of isorule astigmatism increases with spherical ametropia. Axis symmetry is a common feature in bilateral astigmatism in the population, and the prevalence of mirror symmetry is higher than direct symmetry. Axis symmetry usually reduces at older ages, and the least symmetry is seen after the age of 50 years. Most cases of isorule astigmatism are with-the-rule (WW) and the majority of symmetric axes are also in this group, while the isorule oblique type is uncommon in the population and the cases show less symmetry. The rarest form of isorule astigmatism is oblique astigmatism with direct symmetry.
FundingThis project was supported by Shahid Beheshti University of Medical Sciences.
Conflicts of interestThe authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.