Artificial Intelligence, Data Science and E-health in Vision Research and Clinical Activity
More infoTo discriminate suspect glaucomatous from control eyes using corneal densitometry based on the statistical modeling of the pixel intensity distribution of Scheimpflug images.
MethodsTwenty-four participants (10 suspect glaucomatous and 14 control eyes) were included in this retrospective study. Corneal biomechanics was assessed with the commercial Scheimpflug camera Corvis ST (Oculus). Sets of 140 images acquired per measurement were exported for further analysis. After corneal segmentation, pixel intensities corresponding to different corneal depths were statistically modeled for each image, from which corneal densitometry in the form of parameters α (brightness) and β (homogeneity) was derived. After data pre-processing, parameters α and β were input to six supervised machine learning algorithms that were trained, tested, and compared.
ResultsThere exists a statistically significant difference in α and β parameters between suspect glaucomatous and control eyes (both, P < 0.05/N, Bonferroni). From the implemented supervised machine learning algorithms, the K-nearest neighbors (K-NN) algorithm reached 83.93% accuracy to discriminate between groups only using corneal densitometry parameters (α and β).
ConclusionDensitometry of the anterior cornea including epithelium on its own has the potential to serve as a clinical tool for early glaucoma risk assessment.
Glaucoma is a multifactorial eye condition that is the leading cause of irreversible vision loss.1,2 Until it reaches an advanced stage, glaucoma is an asymptomatic disease, so methods of early diagnosis are needed.3 As glaucoma is a condition that damages the optic nerve, research works aiming toward early glaucoma detection were traditionally focused on the back of the eye, i.e., optic nerve, lamina cribrosa, and retina. However, there exists an increasing interest in investigating the cornea as a target tissue for glaucoma detection and management. The potential role of corneal thickness4,5 and corneal biomechanics6,7 in the assessment of glaucoma risk have been investigated. More recently, different studies have found statistically significant differences in corneal densitometry between glaucomatous and control eyes,7-9 suggesting that corneal densitometry analysis could have clinical applications in the diagnosis and management of glaucoma.
Corneal densitometry is an objective measure of corneal clarity, and it is an indicator of corneal health.10 Scheimpflug-based corneal tomography is considered the gold standard for corneal densitometry assessment, but, to date, it is exclusively available on one single commercial device. To overcome this limitation, our research group introduced a platform-independent methodology based on the statistical modeling of the pixel intensity distribution of Scheimpflug images that correlates very well with traditional densitometry (overall cornea, r = 0.89; P < 0.001).11 The method characterizes corneal densitometry with two different parameters. The first parameter accounts for corneal tissue clarity, as traditional densitometry does, whilst the second parameter accounts for corneal tissue homogeneity. This complete approach toward corneal tissue characterization has proven high accuracy and precision in early keratoconus detection,12,13 overpassing the performance of clinically available systems.12,13 This method also investigated corneal densitometry in minor corneal hypoxia14 and rare genetic conditions.15 Moreover, a previous work, based on Optical Coherence Tomography (OCT), investigated corneal backscatter based on the statistical modeling of the pixel intensity distribution of glaucomatous corneas.16 Their results indicated that glaucoma suspects have similar microstructural corneal tissue properties to those exhibited in glaucoma patients but markedly different from that of healthy controls.16 Consequently, their results suggest that micro parameters related to corneal tissue integrity might be a valuable early glaucoma biomarker.
Additionally, machine learning techniques have repeatedly shown their usefulness in ophthalmology as an objective tool to assist practitioners in diagnosing certain conditions.17-19 Glaucoma detection is one of the ocular pathologies where the most efforts regarding machine learning implementation have been made.17 However, to the best of the authors’ knowledge, corneal densitometry was not previously investigated as a valuable feature for suspect glaucoma detection.
Consequently, the current work aims to investigate whether corneal densitometry parameters estimated from statistical modeling of the pixel intensity distribution of Scheimpflug images, with the support of supervised machine learning algorithms, can successfully discriminate between suspect glaucomatous and control eyes.
MethodologySubjects and data collectionTwenty-four participants (24 eyes) were included in this study. Data was retrospectively collected from a previous study.16 The study adhered to the tenets of the Declaration of Helsinki. Written informed consent was obtained from all participants. They were adult participants (19 females, 5 males) between 51 and 73 years old. The suspect glaucoma group (G) consisted of 10 eyes. The remaining 14 eyes served as the healthy control eyes (C). As age, IOP was similar in both groups. Participants had an IOP of less than or equal to 18.5 mmHg. As this was a retrospective study, participants were classified as suspect glaucoma or control according to the classification done by an experienced ophthalmologist in the corresponding prospective study.16 In that prospective study,16 IOP was assessed with Goldmann applanation tonometry; the optic nerve head, including disc area, rim area, rim volume, cup shape measure, height variation contour, and the mean thickness of the retinal nerve fiber layer was examined using Heidelberg Retinal Tomography (HRT 3; Heidelberg Engineering GmbH, Heidelberg, Germany); visual field parameters including mean deviation and pattern standard deviation with Humphrey Field Analyzer II 750, 24-2 Swedish interactive threshold algorithm (Carl Zeiss Meditec, Inc., Dublin, CA); biometry including the central corneal thickness, anterior chamber depth, axial length, and keratometry was measured with IOLMaster 700 (Carl Zeiss Meditec, Inc., Jena, Germany). Additionally, all participants underwent a comprehensive ophthalmological examination, including corneal biomechanics assessment with the Corvis ST (Oculus, Wetzlar, Germany), a high-speed dynamic Scheimpflug imaging system based on mechanical stimulation of the cornea. Exclusively Corvis ST data, including Scheimpflug images and biomechanical data, were utilized in the current study. Eyes with suspect glaucoma were defined as those with glaucomatous optic disc appearance (i.e., exhibiting disc rim loss or excavation, subjectively assessed optic disc cupping of >0.6, or localized abnormalities of the retinal nerve fiber layer) but normal visual fields. None of the suspects were pharmacologically treated for glaucoma. Healthy controls had healthy optic disc appearance and normal visual field, defined as the absence of glaucomatous and neurologic field defects. Subjects were excluded if they had a history of ocular surgery within 12 months before the study or if they were younger than 40 years with corneal or intraocular disease or neurologic disorders affecting visual fields.
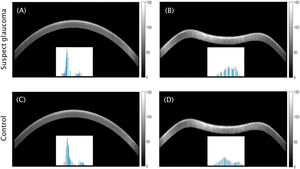
Data analysisImage processing. Parameters α and βCorvis ST corneal deformation grayscale images were obtained every 230 µs and had a fixed size of 576 × 200 pixels, corresponding with an estimated resolution of 14.8 µm/pixel horizontally and 24 µm/pixel vertically. Examples of Corvis ST images along the corresponding corneal histograms are shown in Fig. 1.
Corneal Scheimpflug images after segmentation (i.e. without background) of a randomly chosen suspect glaucoma participant (A, B) and a randomly chosen control participant (C, D); before air-puff (A, C) and during air-puff (B, D). Colour bars indicate pixel intensity. Scaled histograms corresponding to corneal pixels are shown for each image.
After data acquisition, the sets of 140 images acquired per measurement were exported for further analysis, as explained in detail in previous work.12 In short, the method of data analysis consisted of two steps: corneal segmentation and statistical modeling of the pixel intensity distribution. The axial and lateral dimensions of the ROI were optimized to maximize the amount of signal-carrying data or, in other words, to achieve the highest discriminative power between the investigated groups (suspect glaucomatous vs. control eyes). As a preliminary analysis, the horizontal (lateral) dimension of the ROI was fixed to 160 pixels, corresponding approximately to the central 2.5 mm corneal chord. Regarding the vertical (axial) dimension, three different depths were investigated: (1) full corneal thickness, (2) Stroma, and (3) Anterior cornea including epithelium. Consequently, the vertical dimension of the ROI depended on the corneal depth analyzed. Firstly, in the case of considering the full corneal thickness, the number of vertical pixels in the ROI was given by the corneal thickness of each subject, as it was investigated in previous work that corneal thickness is not a co-founding factor affecting the statistical analysis of corneal Scheimpflug images.12 Secondly, when considering the stroma, pixels corresponding to corneal epithelium were omitted, as they carry different statistical information compared to those from the stroma.11 In the third scenario, anterior cornea including epithelium, a fixed vertical ROI of 8 pixels from the detected anterior corneal border, approximately corresponding to the anterior 190 µm, was considered.
The intensity of the pixels corresponding to a given ROI was statistically modeled with the two-parameter distribution functions that were previously used to model corneal Scheimpflug images (i.e., Weibull, Gamma, and Lognormal distributions).12 Output parameters were estimated using the method of maximum likelihood from the pixel intensities of the selected ROI in each image. The goodness of fit was assessed by means of the root mean squared error (RMSE) for the three candidate distributions, as in previous literature.12
As described in previous work in detail,12 the output of the candidate two-parameter distribution functions is two parameters that will be further used to feed the supervised machine learning algorithms. These two parameters are the scale parameter (referred to as α in this work) and the shape parameter (referred to as β in this work). Parameter α accounts for corneal clarity (the larger α, the lesser corneal clarity), while parameter β accounts for corneal tissue homogeneity (the larger β, the greater corneal tissue homogeneity).14 Parameters α and β can have any non-zero positive value.
Cases of study and statistical analysisAs mentioned before, different corneal depths (full cornea, stroma, and anterior cornea including the epithelium) and different statistical models (Weibull, Gamma, and Lognormal distributions) were considered to discriminate between groups (suspect glaucomatous vs. control eyes). Mean group values of α(t) and β(t) parameters under every condition were analyzed. Further, individual values of α and β corresponding to the statistical model and corneal depth that would better discriminate between suspect glaucomatous and control eyes were used to feed the supervised machine learning classification algorithms. In addition, two cases were investigated. Case 1 included α and β estimated from the 140 frames available (i.e., 6720 data points = 2 parameters/frame x 140 frames/participant x 24 participants), while case 2 included α and β estimated from the 20 frames range that showed the best group mean discrimination between groups (i.e., 960 data points = 2 parameters/frame x 20 frames/participant x 24 participants).
Statistical analysis was performed using Microsoft Office Excel (Microsoft Office Professional Plus 2016; Microsoft; Redmond, WA, USA). The normality of each parameter, including α and β per frame and biomechanical parameters, was not rejected (Shapiro–Wilk test, P > 0.05). The independent two-sample t-test was used to assess differences in parameters under evaluation between suspect glaucoma and control groups. The paired two-sample t-test was used to assess differences in α and β parameters between groups. The level of significance was set to 0.05, and a Bonferroni correction was applied to address the problem of multiple comparisons.
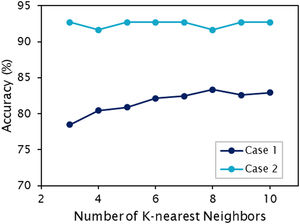
Machine learning classification algorithmsMachine learning classification algorithms were implemented in Python (version 3.8, Python Software Foundation) and were based on the scikit-learn data science library (https://scikit-learn.org). Six supervised algorithms were implemented and tested: (1) Logistic regression, (2) K-nearest neighbors (K-NN) with Euclidean distance and K optimized for each case under investigation (Fig. 2), (3) Kernel support vector machine (SVM) with Gaussian RBF kernel, (4) Naïve Bayes, (5) Decision tree classification, and (6) Random forest classification.
The dataset, imported in .csv format, consisted of two features (α and β) and a labeled output (1 if suspect glaucoma or 0 if control). In case 1 (140 frames) a total of 3360 instances were used as the dataset, while in case 2 (20 frames) a total of 480 instances were used as the dataset.
The architecture of each supervised algorithm follows the same pattern. For data pre-processing, after importing the dataset, missing values were removed. In case 1, 3275 instances remained after missing values depletion (i.e., 2.5% of the whole dataset which was considered acceptable). There was no missing data in the dataset corresponding to case 2.
Each dataset was split into the training set (80 % of the dataset, randomly selected but fixed to train the different algorithms) and the test set (the remaining 20 % of the dataset). This is, in case 1 (140 frames), from the 3275 available instances, a total of 2620 instances were used to train the algorithms, while the remaining 655 instances were used to test the performance of the trained algorithms. Similarly, in case 2 (20 frames), from the 480 available instances, a total of 384 instances were used to train the algorithms, while the remaining 96 instances were used to test the performance of the trained algorithms. Further, feature scaling of α and β based on the standardization technique was applied to the test set and the test set separately in both cases under investigation.
After data pre-processing, each algorithm was trained on the training set and evaluated using the test set. To investigate for potential overfitting each algorithm was also evaluated using the training set. The confusion matrix and the corresponding accuracy (% of correct predictions) were calculated to assess the performance of each architecture. In addition to the statistical analysis, the performance of each test set for each case and architecture was plotted for illustrative purposes.
ResultsBiomechanical parametersParticipants from this study had equivalent mean values of age, IOP, and CCT, as shown in Table 1. No statistically significant difference was found in biomechanical parameters between suspect glaucomatous eyes and control eyes, as indicated in Table 1.
The group statistics for age and biomechanical parameters acquired with Corvis ST: mean values ± SD (range).
No statistically significant differences were found between the candidate functions to fit pixel intensity distribution within the ROI (all pair-wise comparisons, P > 0.05), as indicated in Table 2. The Weibull distribution was chosen to fit the pixel intensity distribution in corneal Scheimpflug images. This choice was motivated for two reasons. One reason is that the Weibull function reported the smallest RMSE (Table 2), even though this difference was not statistically significant. The second reason was to maintain consistency with previous literature where the Weibull distribution function was chosen to fit pixel intensity distribution in corneal Scheimpflug images representing various corneal pathologies12,13,15 and healthy volunteers.11,14
The goodness of fit in terms of RMSE of the different candidate models to fit corneal pixel intensity distribution, expressed in arbitrary units, for 10 suspect glaucomatous eyes and 14 control eyes.
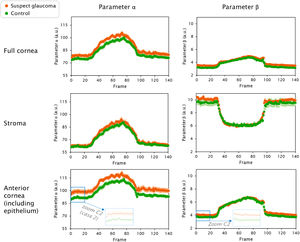
The mean parameters α(t) and β(t) were good discriminators between suspect glaucoma and control eyes (Fig. 3), with statistically significant differences for both α (t) (paired t-test, P < 0.05/N [N = 140, Bonferroni]) and β(t) (paired t-test, P < 0.05/N [N=140, Bonferroni]). This was a good indicator that α(t) and β(t) could serve as discriminators between groups. Hence, case 1 of the study used α(t) and β(t) parameters estimated from 140 frames. However, from the analysis of the three investigated corneal depths and the dynamic evolution of α(t) and β(t) it was concluded that the best discrimination between groups was achieved when analyzing the first frames of the cornea; this is, before mechanical stimulation, as illustrated in Fig. 3. Consequently, individual values of α(t) and β(t) corresponding to the first 20 frames of each participant were used as case 2 of the study.
Mean values of the dynamic evolution of α(t) and β(t) parameters, expressed in arbitrary units, extracted from the fitting of Weibull distribution to the pixel intensities of corneal Scheimpflug images for 10 suspect glaucoma participants (orange) and 14 control participants (green). The analysis was done for different vertical (axial) dimensions of the ROI, considering: full corneal thickness (above), stroma excluding the epithelium (middle), and anterior cornea including the epithelium (bottom). Zoom-in is shown in those frames where group differences in α(t) are the largest. Corresponding frames in β (t) are also shown. Corresponding individual data points to the zoomed area were used in case 2 (20 frames). Error bars: SE at 95% confidence level.
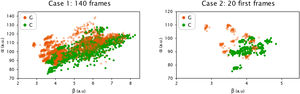
Besides the statistically significant difference achieved in mean α(t) and β(t) between groups, the individual α(t) and β(t) parameters represented messy data, as shown in Fig. 4. Consequently, standard statistics could not help predict whether a new data point would belong to the suspect glaucomatous group or the control group. Therefore, supervised machine learning algorithms needed to be implemented and tested for both study cases separately.
The complete dataset that was used to feed the different supervised machine learning algorithms in each case under investigation. Data points in case 1 correspond to the α(t) and β(t) parameters, expressed in arbitrary units, estimated from the 140 frames available for each subject (3275 data points in total, after removing missing values). Data points in case 2 correspond to the α(t) and β(t) parameters, expressed in arbitrary units, estimated from the first 20 frames collected for each subject (480 data points). For both cases: 10 suspect glaucomatous eyes (G, in orange at 60% transparency) and 14 control eyes (C, in green).
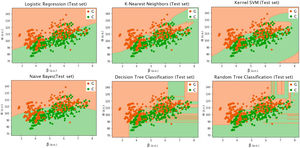
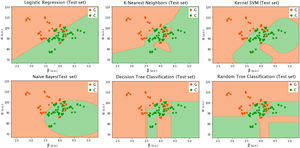
Figs. 5 and 6 illustrate the performance of the implemented supervised machine learning algorithms. The background of the subplots corresponds to the training phase, while the data points correspond to the test set. In other words, suspect glaucomatous eyes (in orange in Figs. 5 and 6) should fall in the orange background while control eyes (in green in Figs. 5 and 6) should fall in the green background, otherwise, there is a misclassification. Corresponding statistics are shown in Table 3. The performance of the algorithms was measured by counting the number of true negatives (number of control eyes correctly classified as control eyes), true positives (number of suspect glaucomatous eyes correctly classified as suspect glaucomatous), false negatives or type II error (number of suspect glaucomatous eyes wrongly classified as control), false positives or type I error (number of control eyes wrongly classified as suspect glaucomatous). Table 4 shows the corresponding statistics for the training set.
Graphical representation of the performance of the different supervised machine learning algorithms in case 1 (140 frames). Background colors represent the output of the training step, while the 655 data points correspond to the test set (i.e., 20% of the total dataset that was not used for training). To clarify, suspect glaucomatous eyes (G, in orange) should fall in the orange background while control eyes (C, in green) should fall in the green background, otherwise, there is a misclassification. Corresponding statistics are shown in Table 3.
Graphical representation of the performance of the different supervised machine learning algorithms in case 2 (20 first frames). Background colors represent the output of the training step, while the 96 data points correspond to the test set (i.e., 20% of the total dataset that was not used for training). To clarify, suspect glaucomatous eyes (G, in orange) should fall in the orange background while control eyes (C, in green) should fall in the green background, otherwise, there is a misclassification. Corresponding statistics are shown in Table 3.
Performance of the trained supervised algorithms on the test set (20% of the whole dataset, i.e., 655 data points in case 1 (140 frames) and 96 data points in case 2 (20 first frames)). Performance was assessed by the number of true negatives (TN), true positives (TP), false negatives (FN), false positives (FP), accuracy, area under the curve (AUC), and 95% confidence interval (CI). The last column (#) orders the algorithms from best performance (1) to worse performance (6).
Performance of the trained supervised algorithms on the training set (80% of the whole dataset, i.e., 2620 data points in case 1 (140 frames) and 383 data points in case 2 (20 first frames)). Performance was assessed by the number of true negatives (TN), true positives (TP), false negatives (FN), false positives (FP), accuracy, and area under the curve (AUC). Corresponding statistics on the test set are shown in Table 3.
Diagnosing early-stage glaucoma is still a clinical challenge. This study shows that it is possible to discriminate, at over 80 % accuracy, suspect glaucomatous from control eyes using corneal densitometry parameters (α – corneal tissue clarity, β – corneal tissue homogeneity) with the support of supervised machine learning algorithms (Figs. 5, 6 and Table 3). The results of the current study are in agreement with those of Iskander and colleagues.16 Using a similar image processing technique as in the present work, they applied statistical modeling of the pixel intensity distribution (i.e., speckle distribution) of commercial OCT images to investigate corneal tissue differences between glaucoma, suspect glaucoma, and control participants. The parameters of OCT speckle can be indirectly linked to the microstructural properties of the imaged tissue.16 Consequently, they showed that the corneal microstructure of suspect glaucoma participants is more similar to that of glaucoma than that of control participants.16
Even though glaucoma primarily affects the optic nerve, as it is a multifactorial disease challenging to detect early, there is an increasing interest in investigating the cornea as a target tissue for glaucoma risk assessment and glaucoma management. In the current work, no statistically significant differences were found in any of the biomechanical parameters analyzed between suspect glaucomatous and control eyes (Table 1). Previous works on corneal biomechanics and glaucoma found a weak relationship between corneal biomechanical parameters and measures of structural and functional damage in glaucoma.6,7 As these correlations were weak and only found in developed cases, corneal biomechanics does not seem to be an adequate biomarker for early glaucoma detection. Consequently, biomechanical parameters were not used to feed the supervised machine learning algorithms in the current work.
Furthermore, recent works suggested that corneal densitometry analysis could have a clinical impact on the diagnosis and management of glaucoma.7-9 Inspired by those previous works, in the current study we investigated corneal densitometry as an early glaucoma biomarker. However, we did not use traditional densitometry values estimated from Pentacam HR software (Oculus, Wetzlar, Germany). Instead, we used Scheimpflug images acquired with Corvis ST. This choice was motivated by the fact that Corvis ST, in opposition to Pentacam HR, allows exporting raw images. In addition, Corvis ST, again contrarily to Pentacam HR, captures Scheimpflug images during the dynamic evolution of the cornea under mechanical stimulation, which allows a more complete analysis of corneal tissue. However, Corvis ST software does not include a corneal densitometry module. Consequently, this study applied an alternative method to traditional densitometry, already validated on corneal Scheimpflug images under mechanical stimulation.20
The method used in the current work to estimate corneal densitometry is based on statistical Weibull modeling of the pixel intensity distribution. Besides giving information on corneal tissue clarity (α parameter), as traditional densitometry does, it offers additional information on corneal tissue homogeneity (β parameter). In previous works investigating corneal densitometry by means of statistical modeling of the pixel intensity distribution, the epithelium was removed,12-14,20 as it is known to carry different statistical information compared to the stroma11 and was therefore considered a potential source of noise. Corneal densitometry is based on light backscatter. As the corneal epithelium and corneal stroma have a different composition, it is expected that light will travel, and consequently scatter, differently in one tissue or the other. Actually, from any standard corneal Scheimpflug image, it is possible to observe bare eye a thin bright layer on the anterior cornea corresponding to the epithelium, while the stroma shows a darker and more uniform appearance. These inner tissue differences justify that when only the stroma was considered, smaller values of α(t) and larger values of β(t) were obtained in the current study, in comparison to the case when the anterior cornea, including the epithelium, was analyzed, as shown in Fig. 3.
In the current study, three different corneal depths were investigated. Various reports have shown that certain glaucoma medications cause alterations in the corneal eye surface.21,22 However, glaucoma is a pathology that does not affect the cornea directly. Consequently, it is not straightforward to predict which corneal depth would be optimal to discriminate the disease. In the current work, the largest separation between suspect glaucomatous and control eyes in the α(t) parameter was found when considering the anterior cornea, including the epithelium. This result shows that even though pixels corresponding to the epithelium carry different statistical information compared to those from the stroma,11 this information might be of value in cases where the discrimination between groups is especially challenging.
In the current research, the group mean parameters α(t) and β(t) were good discriminators between suspect glaucoma and control eyes (Fig. 3), with statistically significant differences for both α (t) (paired t-test, P < 0.05/N [N = 140, Bonferroni]) and β(t) (paired t-test, P < 0.05/N [N=140, Bonferroni]). However, when looking at individual values of α(t) and β(t) parameters, discriminating suspect glaucomatous eyes from control eyes became challenging, as illustrated in Fig. 4. However, the combination of these two parameters, α(t) and β(t), resulted in a successful way to discriminate between suspect glaucomatous and control eyes (Figs. 5, 6, and Table 3) using supervised machine learning algorithms.
In the machine learning part of the study, two different situations were investigated, case 1 (140 frames, 3360 instances) and case 2 (20 frames, 480 instances). The algorithms that showed the best performance were K-nearest Neighbors (case 1) and Decision Tree Classification (case 2). However, as indicated by Table 4, overfitting occurs in the Decision Tree Classification algorithm and consequently should not be considered a good classifier. Overfitting happens when there is a significant difference in accuracy between training and test sets. Overfitting is undesirable as it implies a lack of generalization beyond the training set. Overfitting is one of the main limitations of Decision Tree Classification and Random Forest Classification algorithms.17 Regularization techniques can be applied to solve or minimize overfitting as a part of pre-processing. However, this goes beyond the scope of the current study. Consequently, considering the performance on the training set for cases 1 & 2, and the non-overfitting algorithms, K-NN is the classifier that reached the best performance in the current work (83.93 % accuracy in case 1 and 92.7 % in case 2). K-NN is a supervised algorithm based on the principle that instances of a given dataset generally reside near other instances with similar characteristics.17 The advantages of K-NN include simplicity, speed, and easiness of implementation. The disadvantages of K-NN include not working well with too large datasets or with high dimensions.18 However, these general disadvantages do not apply to the current work, since the dataset used in the training phase was not too large and we were working in two dimensions (only two parameters, α and β, were used to feed the algorithm). Consequently, as the inherent disadvantages of the algorithm were minimized, especially regarding dimensionality, we speculate this might be the reason the K-NN algorithm scored the highest (83.93 % accuracy in case 1 and 92.7 % in case 2).
The main limitation of the current work is the limited sample size. Twenty-four eyes are enough to investigate group means of α(t) and β(t) parameters and traditional statistics can be applied to successfully discriminate between groups, as it was shown in the current work and previous literature.20 However, by definition, machine learning techniques need to learn from a large dataset to be later efficient and achieve high performance. Consequently, 24 eyes is not a sample size large enough to directly apply supervised machine learning methods. To overcome this limitation, instead of using a single α and β per eye (24 instances), we used the complete data available, this is, calculating α and β per eye and frame. Two cases were investigated, case 1 (140 frames, 3360 instances) and case 2 (20 frames, 480 instances). When only considering the 20 first frames, case 2, the highest performance was obtained (92.7 % accuracy), as indicated by Table 3. However, as this data is clustered, as shown in the right part of Fig. 4, this result might be subjected to overfitting. However, in case 1, the performance is still high (83.93 %) and would not be so strongly affected by overfitting. It is also worth mentioning that data quality is often more critical than data quantity to implement a supervised machine learning algorithm successfully.23 Dirty data, i.e., inaccurate, incomplete, or inconsistent data, often leads to misclassifications.23 In the current work, we fed the machine learning algorithms with only two parameters (α and β) that proved to be independent and statistically significant different between control and suspect glaucoma eyes according to traditional statistics. Using clean and meaningful data, as it was done in the current work, enhances the performance and robustness of the training algorithms.23 Nevertheless, future works should repeat the investigation here presented with a larger sample size.
The current study showed that it is possible to extract valuable information from the anterior cornea, including the epithelium, to discriminate suspect glaucomatous from control eyes with 83.93% accuracy. Even though more work needs to be done, with a larger sample size, the presented results shed some light on the investigation of corneal tissue as a clinical tool for early glaucoma detection and glaucoma management. In conclusion, corneal densitometry on its own has the potential to serve as a biomarker for early glaucoma risk assessment.
The authors thank Professor D. Robert Iskander from Wroclaw University of Science and Technology (Poland) for sharing their data.